大口径海底管道JCO成型三维动力分析
谢 鹏,常江涛
(1.中山大学海洋工程与技术学院,广东珠海 519082;2.南方海洋科学与工程广东省实验室(珠海),广东珠海 519082)
0 引 言
海底管道作为海上油气开发必须依赖的重要基础设施,是海洋油气资源开发的生命线。在油气田内部,它将海上油气田的钻井系统、生产系统和海底管汇连成一体,使钻井、采油和输运系统相互关联、相互协调。在油气外输作业中,海底管道跨越复杂海床,与岸基终端设备相连,快速、高效地完成油气的运输过程。近年来,随着世界各国对石油、天然气资源需求量的不断增加,管道作为油气资源输送的主要方式,其生产制造和工程建设技术发展迅猛,且逐渐向大口径的趋势发展。JCO 成型技术作为一种先进的大口径直缝钢管制造工艺,能够根据不同钢级、板宽、壁厚自动调整凸模行程、凸模曲率半径和钢板给进量等生产参数,具有灵活性大、效率高以及成型效果好等优势。管道JCO 成型工艺又称为渐近式多步模压成型法,成型过程一共分为三步。首先,将板坯进行预弯,并将预弯后的板坯由成型机按照预设曲率和步长进行反复压弯,形成横卧的“J”形;再由进给机构逐步将“J”形板坯的另一侧进行多次步进压弯,形成横卧的“C”形;最后在板坯中部压下,使“C”形管坯开口缩小,形成开口的“O”形,JCO 成型工艺过程如图1 和图2 所示。在后续环节中,对“O”型钢管进行合缝、焊接和扩径,并形成最终产品[1-2]。目前,JCO成型管道的钢级最高可达X80级,壁厚最大可达60 mm,管道直径最大可达1800 mm[3]。在大口径海底管道的JCO 成型过程中,既涉及到材料、接触等多种非线性因素,又涉及到“加载-卸载-回弹”循环载荷的作用,力学过程极其复杂。管道凸模行程和凸模曲率半径的参数设置、成型力的精准控制,以及管道成型之后的管道封口形态、残余椭圆度预测,是大口径JCO 钢管制造中的关键技术难题[4-6]。

图1 板坯预弯示意图Fig.1 Pre-bending diagram

图2 JCO成型的三个阶段(该图片出自参考文献[9])Fig.2 Three stages of JCO forming(This picture is from Ref.[9])
国内外学者对JCO成型中的诸多问题开展了研究,总体上可分为两类:一类是以JCO 成型基本变形模式为分析对象,进行管道成型机理和变形规律的研究。2002 年,叶泽刚[7]基于三点弯曲理论将JCO 弯曲分为两种弯曲模式,其一为不对称弯曲模式,其二为对称弯曲模式。分别计算了其受力状态和弯曲板料几何形状,在此基础上开发了JCO 工艺参数设计系统,能够得到较为合理的工艺设计方案。2009 年,李建[8]提出了基于弹塑性幂指数材料模型的弯曲理论,计算精度得到了很大的提高。2010年,高颖[9]分别采用不同的材料模型,以弹塑性理论为基础推导了JCO弯曲变形的相关公式,进一步丰富了弯曲变形理论的研究工作。另一类是以JCO 连续成型为研究对象,进行成型工艺参数的研究。2009年,高颖等[10]建立了采用平截面假定和单向应力假定为基础的弯曲工程理论模型,对钢板弯曲成型进行了静态隐式有限元分析,模拟了X70 管线的JCO 成型过程,得到了最佳凸模下压量以及完整的管坯模型。2010 年,燕山大学的李强等[11]采用连续介质的平面应变四节点减缩积分实体单元CPE4R模拟板坯进行JCO成型仿真研究,通过改变凸模曲率半径得到相应的应力应变场分布情况,以及力与位移曲线的关系。2011年,Chandel和Singh[12]模拟了管道的JCO-E 制造过程,通过改变模具的曲率半径,得出结论:板坯回弹是决定管道成型各个阶段模具曲率半径的一个重要因素,在管道成型的每个工位上,模具的曲率半径对管道的成型起着关键作用。2016年,白图娅等[13]采用二维平面应变有限元模型分析了JCO 成型过程,建立基于径向基函数的代理模型,在此基础上应用遗传算法和灰色系统理论进行了工艺参数的多目标优化设计,实现了减少加工参数,提高生产效率的目标。2019 年,Konstantinos 等[14]对大口径薄壁钢管JCO-E 成型进行了研究,主要集中在合缝焊接与扩径的工艺模拟计算,研究了管坯合缝前形状与尺寸对合缝后残余应力分布的影响以及合缝焊接残余应力对扩径的影响分析,同时表明残余应力在预测管道极限外压和受压弯曲承载力时应予以考虑。2020年,白图娅等[15]通过建立非线性混合强化耦合损伤本构模型,将JCO 成型过程中损伤行为对回弹计算的影响加以考虑,回弹计算结果更加接近实验值,与传统弹塑性模型相比,最大计算误差可以减小约2.8%,提高了JCO 成型过程中的回弹计算精度。综上所述,目前学者们对JCO 成型的研究大多数是为了探索不同成型工艺与管道力学响应之间的内在联系,通过设置不同的生产边界条件,围绕管道的预弯、成型、合缝以及扩径过程中的力学行为进行研究,计算管道成型过程中的应力应变状态,尽可能地提升成型后管道的力学性能。
现有研究大多基于二维有限元模型进行管道JCO 成型分析。这种模型将管道视为轴向无限长,假设管道截面处于平面应变状态,以某一截面的变形代表整条管道。但是由于材料属性、边界效应等非线性影响,二维模型只适用于细长管道(L/D>10)的成型分析,无法对大口径钢管(L/D<10)的成型过程进行准确分析。为解决这一问题,本文基于弹塑性弯曲理论建立了管道JCO成型的“预弯-成型”一体化三维有限元分析模型,利用显式动力学算法研究了规格为Φ1219 mm×22 mm×12 000 mm 的X65直缝焊管JCO 成型过程中的动力学行为,分析了管道沿轴向的不均匀应力应变分布规律,探讨了凸模行程与凸模曲率半径对管道封口形态、应力应变关系和成型力的影响,研究结果为管道JCO 成型过程中的工艺参数优选、力学载荷控制和成型效果评价提供了科学依据和理论支撑。
1 管道成型参数的理论分析
在JCO 成型过程中,凸模下压次数、凸模行程以及每一次下压形成的弯曲角是关键参数。基于前期研究经验及成型设备能力考虑,本文将JCO成型工艺下压次数预设为21次,并假设每一次下压后板坯弯曲角度相同,则可以计算每一次下压的目标弯曲角,如公式(1)所示,

式中,α为目标弯曲角,即每一步成型后板坯的卷曲角度;n为下压次数。J 成型过程板坯的变形示意图如图3所示。
对于规格为Φ1219 mm×22 mm 的管道,设计成型步骤为21 步,可得理论弯曲角度α=16.37°。管道成型后的理论半径可由公式(2)计算,式中,R为理论成型半径,D为管道外径,t为管道厚度。代入数据得R=587.5 mm。

由图3(b)中的几何关系可以进一步计算出下压量h和半步进量l,根据三角形相似定律以及余弦定理可得

图3“J”形变形过程Fig.3‘J’shape deformation process

由式(3)中两式联立即可得凸模行程为

由式(4)即可计算凸模行程h=11.94 mm。在实际工程中,凸模行程应为理论下压量与板坯厚度22 mm 之和。考虑到板坯的回弹效应,在实际生产过程中,凸模行程取值一般大于理论计算值。本文将凸模行程分别取值为32 mm、33 mm、34 mm、35 mm 和36 mm,基于有限元方法进行JCO 成型的三维数值分析,以优选最佳的凸模设置参数。
2 管道成型的有限元分析
2.1 有限元建模
本文以规格为Φ1219 mm×22 mm×12 000 mm 的X65 管线为研究对象,有限元模型包括板坯模型、预弯模具以及成型模具。
板坯模型初始尺寸为3720 mm×22 mm×12 000 mm,采用减缩积分的8节点六面体单元(C3D8R)进行模拟,如图4 所示。ABAQUS 中适用于接触问题的单元须为减缩积分单元[16],该单元适用于接触问题分析,且对模拟非常大的网格扭曲问题有很好的适应性。减缩积分是相对于完全积分来说的,减缩积分单元比完全积分单元在每个方向上少使用一个积分点,在模型受弯曲时可以消除计算中的剪切锁闭问题且对计算结果的精度影响不大。板坯模型共划分为89 200 个单元,单元近似全局尺寸为50 mm;为精确计算回弹,Y方向划分为12 个单元;为了减小计算量,Z方向划分为100个单元。

图4 板坯模型Fig.4 Slab model
预弯模具和成型模具采用减缩积分的4 节点曲面壳单元(S4R)。该单元是一种通用的壳单元类型,具有很好的适应性,既可以用于厚壳问题的模拟,也可以用于薄壳问题的模拟,如图5所示。预弯模具共划分为8952个单元,成型模具共划分为8200个单元,单元近似全局尺寸为50 mm,为了减小计算量,Z方向划分为100个单元。

图5 JCO成型模具Fig.5 Mould of JCO forming
2.2 材料属性
板坯材料采用X65钢材,其材料属性如表1所示。为考虑管道材料的非线性特征,采用Romberg-Osgood方程建立管道材料的本构关系,其表达式为

表1 X65 钢材主要参数Tab.1 Main parameters of X65 steel

式中:ε是材料应变;σ是材料应力;E是弹性模量;σs是屈服强度;A和B是描述材料塑性应变的硬化参数,A=1.29,B=25.58。
2.3 接触设置
板坯与模具之间设置接触面,采用“主控-从属”接触算法。在计算过程中,为了获得较好的模拟结果,一般选取网格较密或者材料较软的表面作为从属表面,因此本模型选择板坯表面作为从接触面,刚体模具表面作为主接触面。接触方向总是与主控表面垂直,计算中沿主控表面的法向传递接触力,沿接触表面的切向传递摩擦力,故接触作用属性设置为法向“硬”接触,切向采用罚函数摩擦公式定义切向摩擦力。
3 管道成型动力过程的数值求解
3.1 求解方法
有限元分析计算方法主要有静力隐式算法和动力显式算法,虽然静力隐式算法有着较好的回弹计算能力,但是考虑到JCO 成型工艺为连续弯曲的多步骤过程,计算时间较长,载荷性质动态变化,更加需要动力显式算法高效的接触功能以及超强的稳定性,故选择动力显式方法进行JCO 成型有限元建模计算。ABAQUS 动力显式算法在整个运算过程中采用中心差分方法求解系统的整体平衡方程,运用动态方程在每个微小的增量步内计算出下一个增量步的动态情况[17]。
假设节点质量矩阵为M,加速度为¨,外力为P,单元所受内力为I,则节点的平衡方程为

根据方程(6)可计算出在当前增量步(t)时的节点加速度为

由于显式求解器所用的质量矩阵为对角矩阵,因此无需求解方程组,节点的加速度完全由节点上的外力以及质量矩阵决定,因此求解过程可以节省大量计算资源。在极短的时间内加速度若为常值则可以采用中心差分方法对加速度积分,并计算节点的速度,其中Δt为初始时间增量步。

在此运算中心差分对速度积分求解出位移方程:

由式(6)~(8)可知,模型中节点位移、节点速度和节点加速度只与初始增量步有关。因此ABAQUS/Explicit以初始时间增量和多个增量步进行中心差分运算。
假设单元应变增量为dε,单元应力为σ,根据应力-应变关系可以得出单元的应力-应变关系为

在ABAQUS/Stander 中进行非线性分析时,每一个时间增量步都需要求解大量的非对角矩阵平衡方程组,极其耗时,且在涉及接触时最容易出现求解不收敛的现象,因而采用ABAQUS/Explicit 进行显式动力学分析,具有节省计算资源、计算速度较快以及精确度较高等优点。
3.2 载荷步设置
管道的JCO 成型过程分为预弯与成型两个阶段。在第一阶段,预弯板边,所有其他板件几乎保持未变形。在预弯过程中,为了提高JCO 成型管道尺寸精度,避免封口处出现“噘嘴”状,需要对板坯两端进行弯曲变形,使其两端曲率达到或者接近成型后钢管的曲率,预弯模型如图6(a)所示,在预弯过程中,上模固定不动,下模向上运动。在第二阶段,分别将管坯压制为“J”形、“C”形和“O”形。JCO 成型包括J 形弯曲、C 形弯曲及O 形弯曲的连续操作。成型过程中凹模固定不动,凸模向下运动一定的行程将板坯压制弯曲一定的角度。模具尺寸及装配位置均按照实际生产设置,模型如图6(b)所示。

图6 板坯与模具的初始装配关系Fig.6 Schematic diagram of the initial setup of blank and punch
为了精确模拟管道的成型过程,在有限元分析中通过载荷步分解,实现管道成型的连续分析,在管道弯曲成型过程中,共需一次预弯、21次成型压制。每个成型道次包括三个步骤,分别为板坯步进、加载和卸载。具体的载荷步如下所示:
(1)预弯。在此分析步中,上模固定不动,下模向上运动,将板坯两端预弯至一定的曲率。
(2)板坯步进。在此分析步中,给板坯施加位移载荷,模具完全固定,将板坯移动到合适的位置,为加载步做准备工作。
(3)加载。在此分析步中,凹模完全固定,板坯长度方向上固定z方向的位移以及绕x、y轴的转动,板坯宽度方向固定x方向的位移以及绕y、z轴的转动,凸模只允许向下的位移。
(4)卸载。在此分析步中,凹模和板坯的边界条件与加载时相同,凸模只允许向上的位移。
(5)重复上述(2)~(4)载荷步,经过10 个道次的压制,板坯形成“J”形,此时将板坯未经过压制的一段送入模具,再经过10个道次的压制,板坯形成“C”形,最终压制板坯中部,形成开口的“O”形。
3.3 分析结果
图7为管道成型过程示意图。在制造过程的每个阶段,为了达到最终的形状,板坯在不同的区域发生变形。板坯首先在预弯阶段,经过两端的预弯模具将板坯两端弯曲一定的曲率;预弯完成后的板坯进入成型阶段,通过多次压制步骤将板坯压制为“J”形,接着从另一侧压制板坯直到获得“C”形;最终压制板坯中部使其呈开口的“O”形。

图7 预弯与JCO成型过程数值模拟结果(21道次,h=34 mm,R=280 mm)Fig.7 Numerical simulation of the crimping and JCO forming process(21 punching steps,h=34 mm,R=280 mm)
成型后管坯等效塑性应变云图如图8所示,板坯经过预弯以及21个道次的下压过程后,形成了一段长12 m 且带有开口的圆形管道。等效塑性应变沿管道轴向分布不均匀,呈现连续且周期性变化。这些应变不均匀区域处于同一直线上,都是经过同一次”下压-回弹“过程产生的,这说明在下压过程中管坯既产生了轴向变形也产生了周向变形,因此导致了管坯回弹后应力应变的轴向分布不均匀。为了直观显示轴向应力应变分布情况,取长度为1000 mm 的管道来分析管道JCO 成型的“加载-卸载”过程。计算结果如图9 所示,加载后,管坯的应力在轴向上分布是均匀的,此时最大应力为494 MPa;卸载后,残余应力以及等效塑性应变均随着管坯轴向呈周期性分布,与图8 中的应力、应变较大区域对应。

图8 成型后管坯示意图Fig.8 Schematic diagram of the pipe after forming
取图9 中方框内一个波峰与波谷探究管坯残余应力及等效塑性应变轴向分布不均匀的变化程度,在距离管坯截面475 mm 处,残余应力达到最大值325.93 MPa,在距离管坯截面600 mm处,残余应力随轴向逐渐降低至最小值271.39 MPa,降低幅度达16.73%;相应地,等效塑性应变由最大值0.0512 逐渐降低至最小值0.0481,降低幅度达6.05%。由此可知,在JCO 成型对管坯轴向应力应变分布不均匀的影响中,应力的不均匀分布特性更为显著。
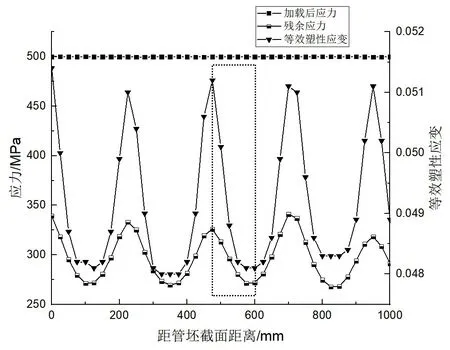
图9 管坯轴线方向应力应变曲线Fig.9 Stress and strain curve of the pipe in axial direction
成型力是JCO 成型过程中的重要参数,既关系到JCO 成型设备的承载能力,也与管道的最终成型效果密切相关。图10 是JCO 成型过程中,21 次下压过程中凸模成型力的变化曲线,其中凸模行程h=34 mm,曲率半径R=280 mm。由图10 可知,成型力基本处于3.75×107~4.25×107N 范围内,各道次成型力有所波动,但整体变化不大。其中,第1、第2以及第11、第12道次的成型力较小,这是由于这几个成型道次靠近管坯边缘,而管坯边缘经过预弯后本身带有一定的曲率,因此成型力相对较小。
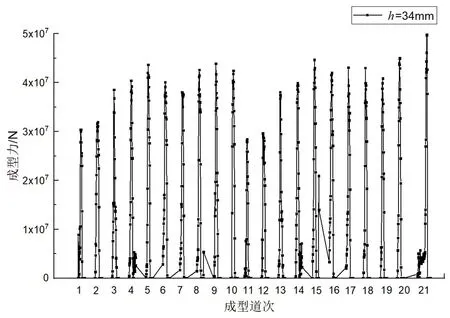
图10 JCO成型过程成型力变化曲线Fig.10 Forming force in the progress of JCO forming
为了分析下压回弹后管坯的应力应变分布情况,选取位于凸模正下方、板坯上表面的一个节点来分析管坯单次“下压-回弹”过程中的应力应变历程,结果如图11所示。在下压过程中,由于凸模不断下移,板坯发生弯曲变形,因此板坯的应力逐渐增大直至加载结束达到最大值494 MPa;在0点到B点之间,板坯的等效塑性应变值始终为零,说明板坯的变形处于弹性变形阶段,B点以后,随着凸模继续下移,板坯开始进入塑性变形阶段,板坯的等效塑性应变逐渐增大直至加载结束达到最大值0.042;在回弹过程中,板坯的应力逐渐减小至A点后趋于平稳,A点后的板坯应力称为残余应力,其值为273 MPa,相较于最大应力降低了44.7%,板坯等效塑性应变是由板坯发生塑性变形产生的,因此在回弹过程中不发生变化。

图11 管坯单次“下压-回弹”过程中的应力应变历程Fig.11 Stress and strain history in the process of single‘pressing-springback’of pipe
4 凸模行程对管道成型效果的影响
管道成型后的应力、残余应力、应变场和成型力等参数是衡量管道成型效果的重要参数,是JCO成型是否符合实际生产的衡量标准。这些参数影响着成型后管道的强度、刚度以及稳定性,需要进行系统的计算分析。因此本文以凸模行程和曲率半径作为主要变量,对JCO 成型主要参数进行分析。固定凸模曲率半径为R=280 mm,通过选取不同的凸模行程来分析板坯JCO 成型情况,具体取值见表2;得到5组JCO成型结果,如图12所示。

表2 凸模行程取值Tab.2 Values of punch stroke
4.1 管道的封口形态
如图12 所示,在相同的凸模曲率半径下,随着凸模行程的增大,管坯成型后的开口距离逐渐减小。表3 给出了管坯的几何形状参数,分析了管坯的椭圆度、开口宽度以及“撅嘴”量,并与同样条件下的工厂实际生产管道参数做对比。结果显示,当凸模行程h=32 mm 时,由于压制量不足,导致成型后管道出现较大的开口以及明显的“噘嘴”现象;当凸模行程h=36 mm 时,由于压制过量,成型后管道两端出现重叠部分;当凸模行程h=34 mm时,成型后管道的几何参数较好,椭圆度、开口量以及“噘嘴”量都在工厂实际生产范围内,能够满足实际的生产要求。
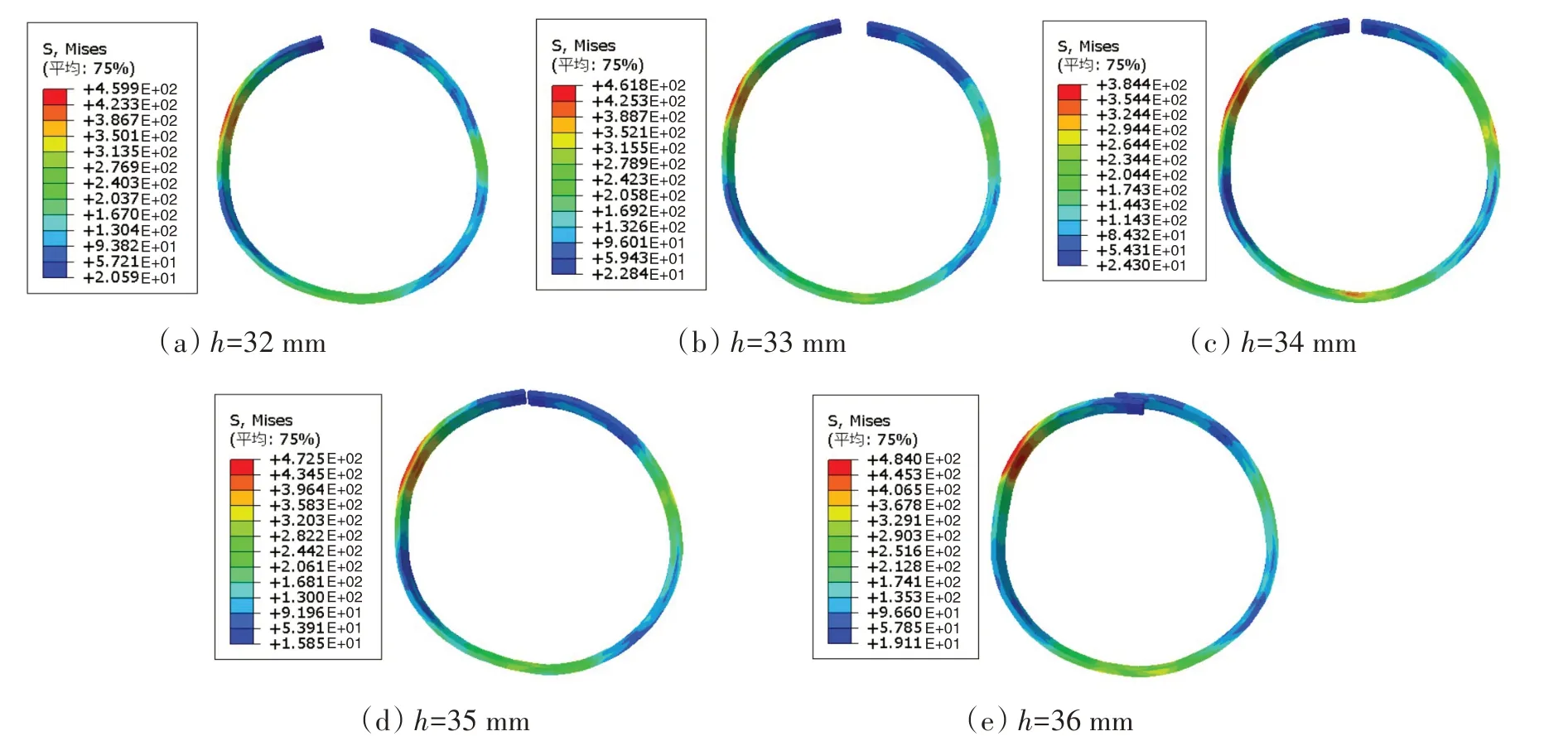
图12 不同凸模行程下JCO仿真结果Fig.12 Simulation results of JCO with different punch strokes

表3 不同凸模行程下管坯几何形状Fig.3 Geometries of pipe with different punch strokes
4.2 管道成型力
在管道成型过程中,模具对板坯进行多次冲压,在这个过程中JCO 成型设备需要提供巨大的压力来使板坯弯曲到一定曲率,由生产设备提供并作用到板坯上的力即为“成型力”。成型力在JCO 成型过程中是不断变化的,时刻影响着设备的加工能力、设备安全以及稳定性;同时,成型力的大小也是管道成型质量控制的重要参数和评估依据。
图13(a)给出了在不同凸模行程下,模具在单次加载到卸载过程中成型力的变化曲线。随着凸模行程的增大,成型力也随之增大,当h=32 mm时,最大成型力为3.62×107N,当h=36 mm时,最大成型力为4.65×107N,凸模行程增大了4 mm,成型力增幅高达28.5%;加载时,成型力逐渐增大,卸载时,成型力迅速减小,由于加载后管坯出现了塑性变形,因此管坯回弹到A点后就不再回弹,而凸模继续卸载与板坯分离,此后成型力为0。图13(b)给出了凸模行程h=34 mm 时的凸模和两凹模成型力,左右两凹模成型力几乎相同,凸模成型力与两凹模成型力方向相反,前者大小为后两者之和。

图13 单次“加载-卸载”过程中模具成型力Fig.13 Mold forming force in single‘loading-unloading’process
4.3 管道应力和残余应力
由于JCO 成型过程步骤较多,因此选取其中一个道次进行应力应变分析。压制过程分为加载过程和卸载过程,应力应变因弹性回复会发生较大的变化,管坯的残余应力仿真结果如图14所示。

图14 应力场及数据采集路径Fig.14 Stress and data acquisition path
如图14 所示,卸载后管坯内仍然存在较大的残余应力,随着凸模行程的增大,压制范围增加,残余应力场区域增大。在弯曲对称轴上采集节点数据,并绘制沿厚度方向的应力、残余应力分布曲线,如图15所示。

图15 不同凸模行程下管坯的应力、残余应力曲线图Fig.15 Stress and residual stress curve in different punch strokes
如图15(a)所示,随着凸模行程的变化,加载后管坯应力的最大值始终出现在板坯上下边界部位,最小值始终出现在板坯中性层附近,在板坯内外层附近,管坯的应力变化较为平缓;但在中性层附近,管坯的应力出现急剧变化。凸模行程h=32 mm时最大应力值为491 MPa,凸模行程h=36 mm时最大应力值为495 MPa,最大应力增幅仅为0.8%,变化不大,说明不同凸模行程对板坯应力的影响较小。板坯的残余应力曲线如图15(b)所示,在板坯内外层附近,随着凸模行程增大,板坯的残余应力值逐渐减小,凸模行程h=32 mm、33 mm、34 mm时,板坯上表面残余应力值为分别为350 MPa、290 MPa、250 MPa,凸模行程每增大1 mm,板坯残余应力的降幅分别为17.14%、13.80%,可知残余应力的降低幅度逐步减小。凸模行程h=36 mm时,板坯上表面残余应力为227 MPa,相较于h=32 mm时降低幅度达到35.14%,板坯内外层的残余应力值对凸模行程的变化较为敏感。在中性层附近,随着凸模行程增大,残余应力值随之增大,h=32 mm、36 mm时,最大残余应力值分别为275 MPa、304 MPa,凸模行程增大4 mm,板坯残余应力值增幅仅为10.5%,残余应力值变化较板坯内外层附近更加平缓,应力分布趋于均匀。
4.4 管道应变分析
JCO 成型管坯最终形状主要取决于成型过程中的塑性应变。在板坯的弯曲对称轴上采集等效塑性应变数据,如图16(a)所示,可以得到不同凸模行程下沿厚度方向的等效塑性应变,如图16(b)所示。

图16 等效塑性应变场及数据采集路径Fig.16 Equivalent plastic strain field and data acquisition path
如图16(b)所示,在板坯对称面内外层附近,随着凸模行程增大,等效塑性应变值增大,当h=32 mm 时,板坯上表面等效塑性应变为0.04;当h=36 mm 时,板坯上表面等效塑性应变为0.043,增幅达7.5%;在中性层附近,等效塑性应变值均趋近于0;凸模行程越小,等效塑性应变变化幅度越小,成型更加均匀。
5 凸模半径对管道成型效果的影响
凸模曲率半径作为JCO 成型工艺中的重要参数,对管道成型质量以及设备的承载能力有着重要影响。固定凸模行程h=34 mm,通过选取不同的凸模曲率半径来分析板坯的JCO 成型情况,具体取值见表4;得到5 组JCO 成型结果,如图17所示。

表4 凸模曲率半径取值Tab.4 Values of punch radius
5.1 管道的封口形态
如图17 所示,在相同的凸模行程下,随着凸模曲率半径的增大,管坯成型后的开口距离逐渐增大。表5 给出了管坯的几何形状参数,分析了管坯的椭圆度、开口宽度以及“撅嘴”量,并与同样条件下的工厂实际生产管道参数做对比。结果显示,当凸模曲率半径R=200 mm 时,管道开口量最小为22.2 mm;当凸模曲率半径R=360 mm 时,管道开口量最大为219.2 mm;当凸模曲率半径R=280 mm 时,成型后管道的几何参数较好,椭圆度、开口量以及“噘嘴”量都在工厂实际生产范围内,能够满足实际的生产要求。

图17 不同凸模曲率半径下JCO仿真结果Fig.17 Simulation results of JCO with different punch radii

表5 不同凸模曲率半径下管坯几何形状Fig.5 Geometries of pipe with different punch radii
5.2 管道成型力
为了探究不同凸模曲率半径对成型力的影响,给出了不同凸模曲率半径下凸模成型力随成型进度的变化曲线,如图18 所示。结果显示,随着凸模曲率半径的增大,管坯压制范围增大,凸模成型力急剧增大,当凸模半径R=200 mm 时,成型力为3.10×107N;当凸模半径R=360 mm 时,成型力为6.25×107N,增幅高达101.6%,凸模曲率半径的改变对成型力的影响相较于凸模行程更为显著。较大的凸模曲率半径意味着生产时需要更大的能耗,因此在实际生产过程中,应当根据凸模成型力和管道成型效果优化生产参数。
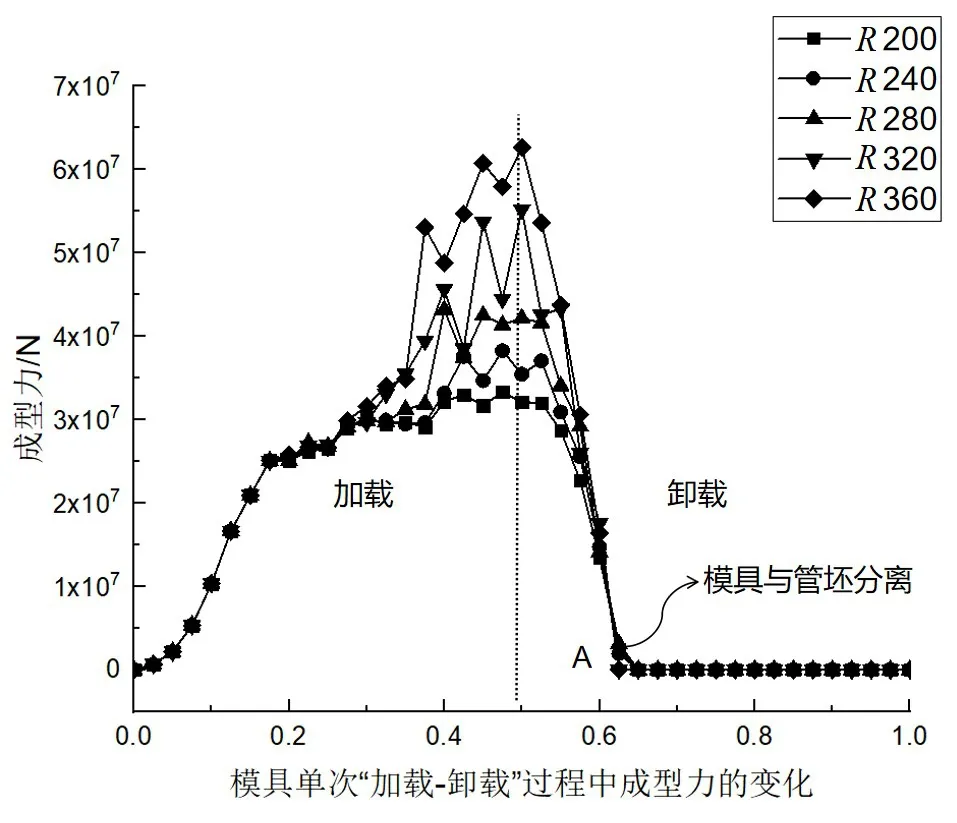
图18 不同凸模曲率半径下凸模成型力曲线Fig.18 Forming force curve for different punch radii
5.3 管道应力和残余应力
板坯在压弯卸载前后发生较大的回弹,材料应力应变也会随之发生剧烈变化。图19 给出了管坯加载后与卸载后的应力场.结果显示,随着凸模曲率半径的增大,管坯压制范围增大,管坯残余应力区域增大。在弯曲对称轴上采集节点数据,并绘制沿厚度方向的应力、残余应力分布曲线,如图20所示。

图19 管坯的残余应力场Fig.19 Residual stress of pipe
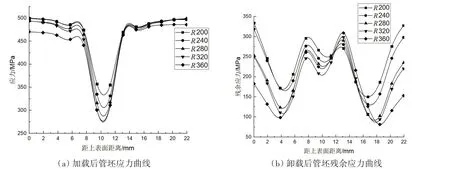
图20 不同凸模曲率半径下管坯的应力、残余应力曲线图Fig.20 Stress and residual stress curve for different punch radii
如图20(a)所示,随着凸模曲率半径的增大,管坯最大应力减小;曲率半径R=200 时最大应力为498 MPa,曲率半径R=360 时最大应力为468 MPa,降低幅度达6.02%;最大应力均出现在板坯内外层附近,最小应力出现在中性轴附近。由图20(b)所示,在板坯内外层附近,随着凸模曲率半径增大,板坯的残余应力值逐渐减小,凸模曲率半径R=200 mm 时,板坯上表面残余应力为335 MPa;凸模曲率半径R=360 mm 时,板坯上表面残余应力为180 MPa,降低幅度达到46.27%,板坯内外层的残余应力值对凸模行程的变化更为敏感。在中性层附近,随着凸模行程增大,残余应力值变化较为平缓,当R=200 mm、360 mm 时,最大残余应力值分别为270 MPa 和315 MPa,凸模行程增大4 mm,板坯残余应力值增幅为16.67%,应力分布趋于均匀。
5.4 管道应变分析
JCO 成型管坯最终形状主要取决于成型过程中的塑性应变。在板坯的弯曲对称轴上采集等效塑性应变数据,可以得到不同凸模曲率半径下沿厚度方向的等效塑性应变,如图21所示。结果显示,在板坯对称面内外层附近,随着凸模曲率半径增大,等效塑性应变值减小,当R=200 mm 时,板坯上表面等效塑性应变为0.047;当R=360 mm 时,板坯上表面等效塑性应变为0.0365,降幅达22.34%,;在中性层附近,等效塑性应变值趋近于0;凸模曲率半径越大,等效塑性应变变化幅度越平缓,成型更加均匀。

图21 不同凸模曲率半径下管坯等效塑性应变分布曲线Fig.21 Equivalent plastic strain for different punch radii
6 结 论
本文围绕大口径海底管道制造的关键技术问题,基于理论分析和数值仿真方法对管道JCO 成型的动力学过程进行研究,讨论了影响管道成型效果的主要参数,得到以下结论:
(1)三维有限元分析方法可以准确模拟大口径海底管道的JCO成型过程,为管道成型参数的优选提供理论依据和科学支撑。
(2)在JCO成型过程中,不同载荷步中,管道成型力大小不相等,与凸模下压位置有关。在距离板坯边缘较近的位置,所需要的成型力较小,反之则较大。
(3)使用JCO成型后的管道残余应力和等效塑性应变沿着轴线分布不均匀,且沿轴线呈周期性变化,在距离管坯截面475~600 mm 范围内,残余应力与等效塑性应变的降低幅度分别达到16.73%和6.05%,残余应力的轴向不均匀变化程度相较于等效塑性应变更加显著,这是以往的二维有限元模型无法求解和分析的。
(4)在一定的凸模行程范围内,随着凸模行程的增大,管坯成型后开口距离明显降低,每一道次的应力、应变场区域增大,成型力增幅高达28.5%,板坯内外层残余应力值降低,降低幅度为35.14%,板坯中性层附近区域残余应力值增大,增幅为10.5%,应力值变化更加平缓,应力分布趋于均匀。
(5)在一定的凸模曲率半径范围内,随着凸模曲率半径的增大,管坯的应力、应变场区域有所增大,成型力增幅高达101.6%,板坯内外层残余应力值降低,降低幅度为46.27%,板坯中性层附近区域最大残余应力值增大,增幅为16.67%,应力值变化更加平缓,变形更加均匀,但是所需的成型力较大。因此在实际生产中应选取合适的凸模行程与凸模曲率半径,提高管道JCO成型质量,同时降低能耗。

