一类具有消失χ 曲率的(α,β)-度量∗

麻翠玲，张晓玲†，何 勇

(1.新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830017;2.新疆师范大学 数学科学学院,新疆 乌鲁木齐 830053)

0 引言

在芬斯勒几何中有许多的非黎曼量(即在黎曼几何中恒为零,但在芬斯勒几何中未必为零的几何量),例如:S 曲率,Berwald 曲率,Landsberg 曲率,χ 曲率,H 曲率,E 曲率等.研究这些特殊曲率的性质往往能够得到一些整体性结果,因此具有十分重要的意义[1−2].

设(M,F) 是n 维芬斯勒流形,切丛TM 上的非黎曼量χ=χidxi定义为

其中:S 表示S 曲率,“.” 和“;” 分别表示F 关于陈联络的竖直协变导数和水平协变导数.

文献[2]研究了旗曲率与χ 曲率之间的关系,证明了具有标量旗曲率的芬斯勒度量具有几乎消失χ 曲率当且仅当旗曲率几乎消失.特别地,具有消失的χ 曲率当且仅当旗曲率消失,并证明了Randers 度量的S 曲率几乎迷向当且仅当χ 曲率几乎消失.文献[3]给出了Kropina 度量具有几乎消失χ 曲率的等价条件.文献[4]给出了(α,β)-度量χ 曲率的具体表达式,并发现对于具有几乎消失χ 曲率的m(≥2) 次多项式(α,β)-度量,其χ 曲率一定消失,且在共形平坦条件下,F 一定是局部闵可夫斯基度量.文献[5]刻画了一类具有消失χ 曲率的广义(α,β)-度量,并研究了球对称度量的相关性质.

文献[6]研究了χ 曲率与Ricci 曲率之间的关系,并由此发现了一类新的非黎曼量.之后,他们证明了对于具有标量曲率的喷射,其具有迷向曲率当且仅当χ 消失[1].沈忠民近期讨论了χ 曲率关于喷射G 的几种不同的表达式,证明了用S 曲率进行射影变换得到的喷射总是具有消失的χ 曲率,并在χ=0 的条件下建立了有关喷射的Beltrami 定理.

(α,β)-度量是一类特殊的芬斯勒度量,表示形式如下

在本文中我们研究了一类具有消失χ 曲率的(α,β)-度量,并得到如下定理.

定理1设F=αφ(s) 是n(≥3) 维流形M 上的非黎曼(α,β)-度量,如果β 满足

其中:∊=∊(x) 是标量函数,那么χ=0 等价于下列三个条件之一成立:

(a) ∊=0,

其中

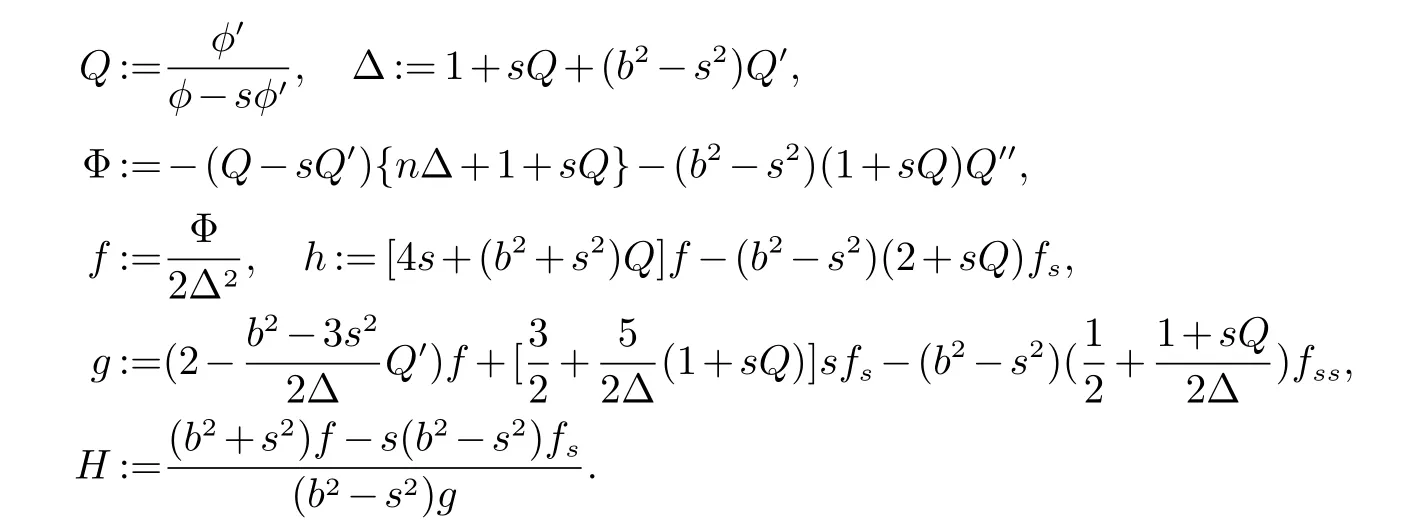
注记1文献[4]证明了具有几乎消失χ 曲率的多项式(α,β)-度量,其χ 曲率一定消失,未进一步研究具有消失χ 曲率的多项式(α,β)-度量.本文研究了一般的(α,β)-度量,而不只是多项式(α,β)-度量.文献[5]研究了广义(α,β)-度量.在其中c 为常数的条件下,刻画了其具有消失χ 曲率的性质.

注记2注意到

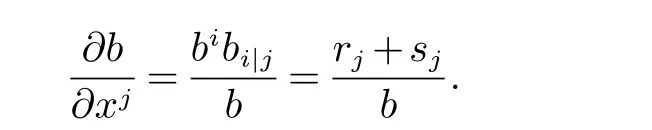
因此b 为常数的充要条件是rj+sj=0.如果β 满足式(2),我们有rj+sj=0,即b 为常数.

注记3对于多项式(α,β)-度量,令h=0,F 退化为黎曼度量,见定理3.

注记4对于多项式(α,β)-度量,令g=0,用Maple 程序计算得,当2 ≤k ≤5 时,F 均退化为黎曼度量.

注记5对于形如式(3)、式(4)的多项式(α,β)-度量

1 预备知识

设M 是一个n(≥2) 维光滑流形.切丛TM 上的点记为(x,y),其中:x ∈M,y ∈TxM.令(xi,yi) 是TM 的局部坐标,上的函数F :TM-→(0,+∞) 称为芬斯勒度量,如果其满足以下几个条件:

(1) F 在TM {0} 上是光滑的；

(2) 对任意的λ＞0,F(x,λy)=λF(x,y)；

(3) 基本二次型为g=gij(x,y)dxi⊗dxj,其中:

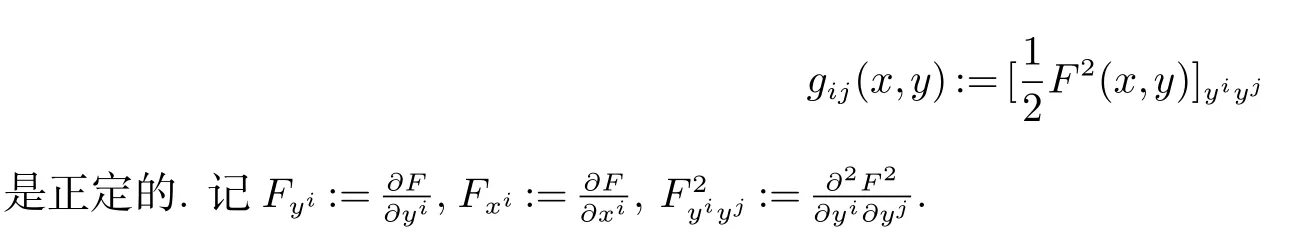
设F 是n 维流形M 上的一个芬斯勒度量,F 的测地系数Gi定义为

其中:(gij)=(gij)−1.

设dV=σ(x)dx 是M 上的体积形式,那么S 曲率定义为

其中:bi|j表示β 关于α 的共变导数.

2 一类(α,β)-度量的χ 曲率

引理1[7]设F=αφ(s) 是n 维流形上的一个(α,β)-度量.如果β 满足式(2),那么其S 曲率为

利用引理1 和式(1),我们得到定理2.

定理2设F=αφ(s) 是n 维流形上的一个(α,β)-度量.如果β 满足式(2),那么

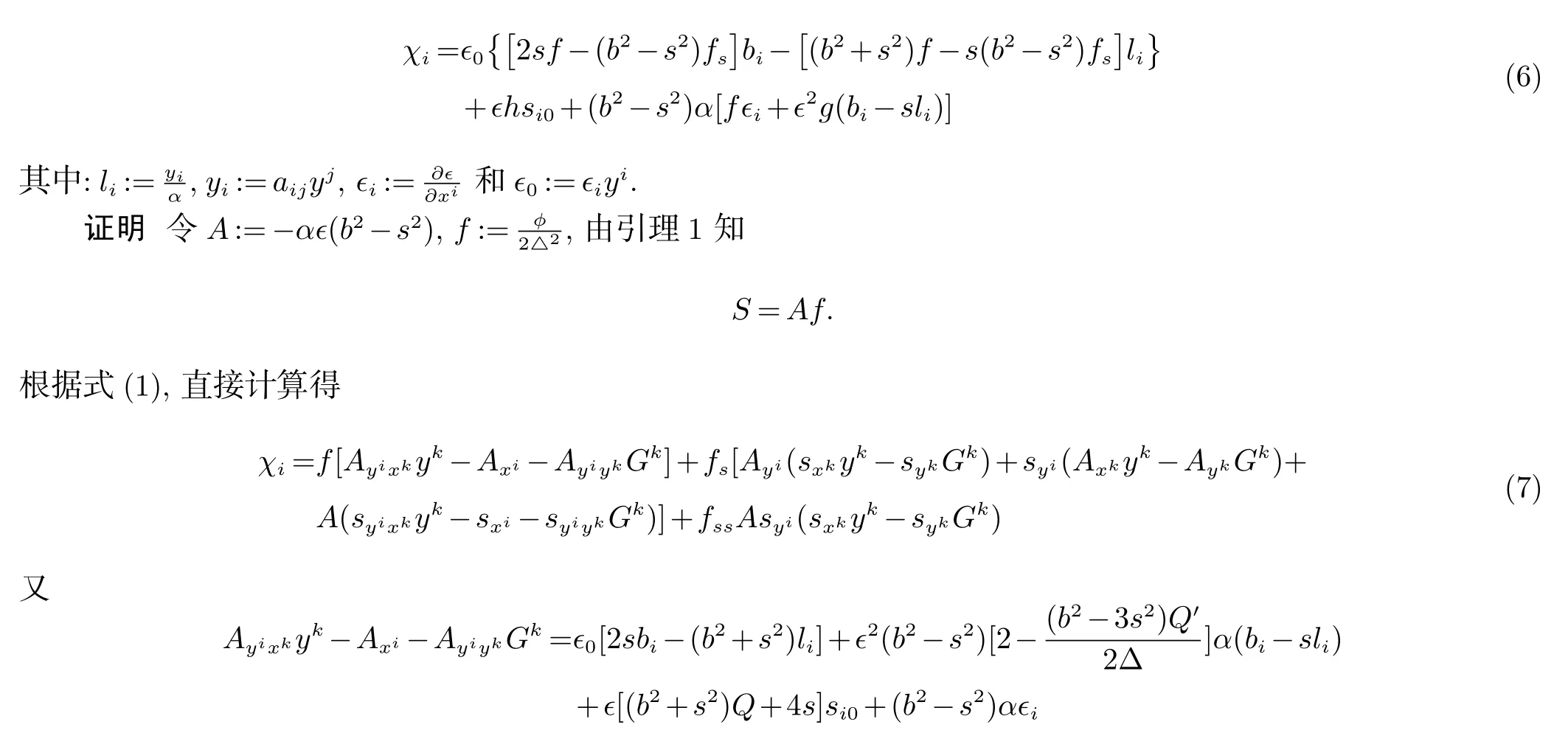
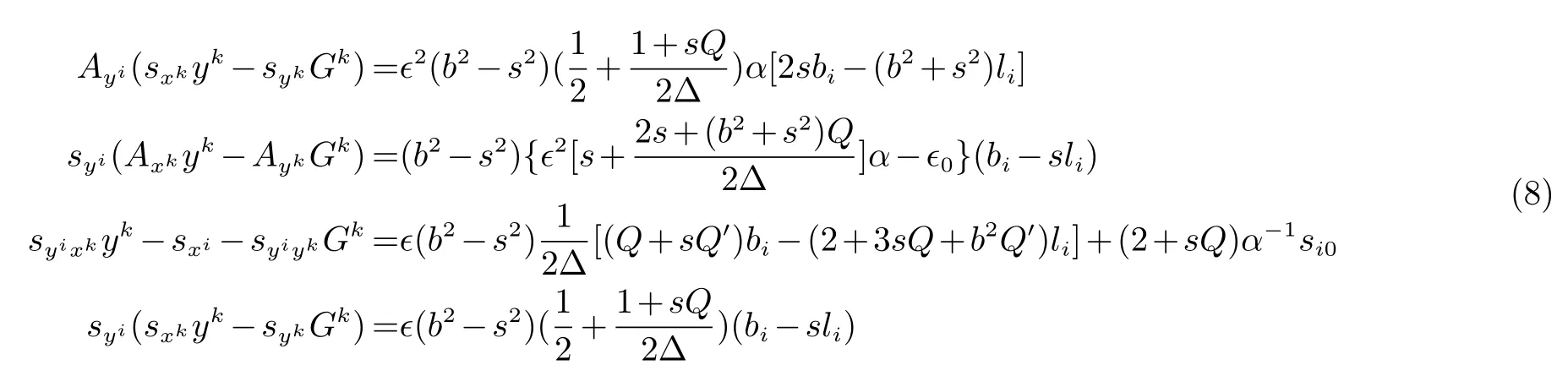
将式(8) 代入式(7),即得式(6).

3 一类具有消失χ 曲率的(α,β)-度量

本节将给出定理1 的证明.

定理1 的证明

当f=0 时,F 为黎曼度量,因为文献[8]已证明(α,β)-度量是黎曼度量当且仅当Φ=0.

当∊=0 时,χi=0 显然成立.因此下述分析中考虑∊/=0 且f/=0 的情况.

当∊是非零常数时,由式(6) 得

上式用bi缩并,得

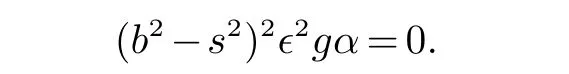
从而g=0.代入式(9) 得,h=0 或sij=0.

当∊不是常数时,为了简化计算,我们在x 点的切空间TxM 上取关于α 的正交基,使得

并且在TxM 上取适当的坐标变换ψ:(s,uA)→(yi):

对上式的下标i,分别取i=1 和i=A,可得根

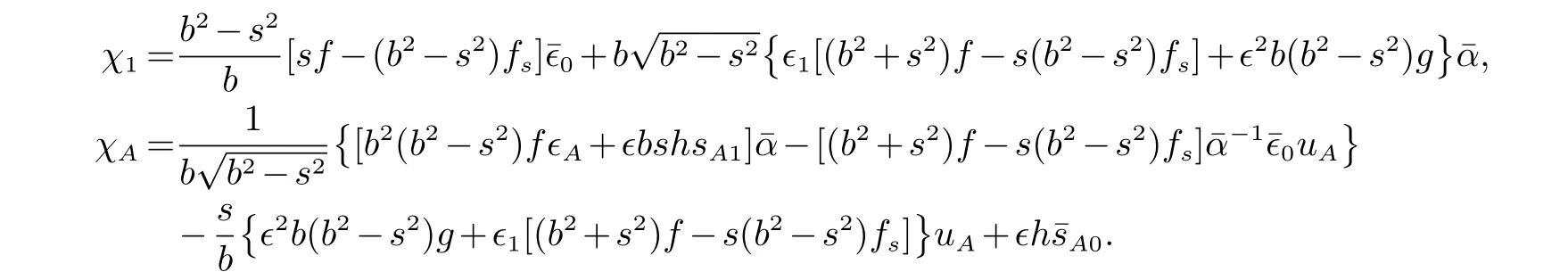
据χ1和χA关于uA的有理项和无理项,χi=0 等价于下列四式成立

对式(12) 关于uB,uC求导,得

在式(14) 中,令A=B,并取迹,得

类似地,在式(14) 中,令B=C,并取迹,得

由(n-1)×(15)-(16),得

因此,当n ≥3 时,∊A=0.

此时,式(10) 自然成立,且式(11) 可转化为

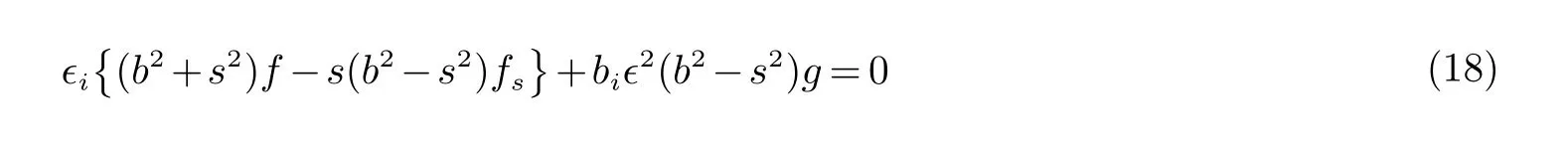
由式(18) 的表达式可知,若g=0,则

方程(19) 的非零解为

其中:µ 是任意常数.将式(20) 代入g=0,得

方程(21) 的解为

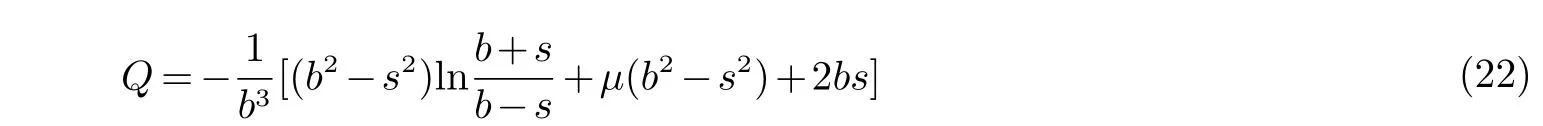
将式(22) 代入f 的表达式,可得

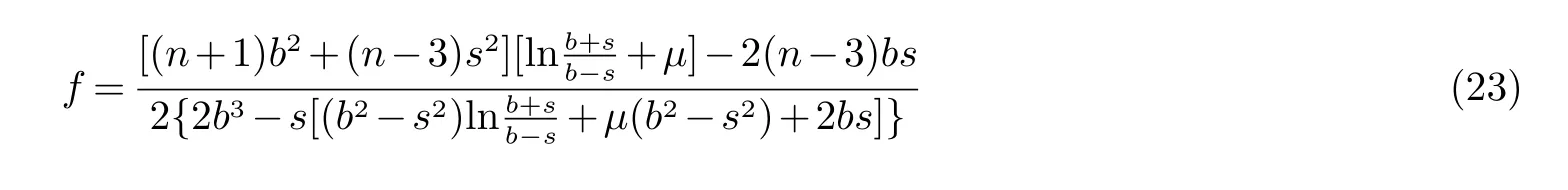
这与式(20) 矛盾.因此g 恒不为零.

从而,由式(18) 可得

则Hs=0,即H 为任意非零常数.从而,由(24) 式知sij=0,此时式(13) 自然成立.反之,若F 满足定理1 中的条件(a) 或(b),则显然χ 曲率消失.对于情形(c),知

将以上两式代入定理2 的(6) 式,则式(6) 恒成立.

例1解方程sf-(b2-s2)fs=0,得则当时,由定理1 中的(c) 可知,满足此条件的(α,β)-度量具有消失的χ 曲率.

对于k(≥2) 次多项式(α,β)-度量,即F=αφ(s),其中:φ(s)=1+a1s+a2s2+···+aksk.我们有如下定理.

定理3设F=αφ(s) 是n(≥3) 维流形上的(α,β)-度量,其中φ(s) 是关于s 的k(≥2) 次多项式.如果h=0,那么F 为黎曼度量.

证明对h=0 乘以2Δ3(φ-sφ′)8,由最高次项系数为零,得

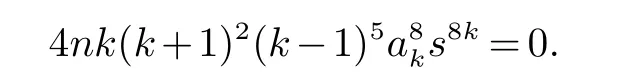
则ak=0.从而

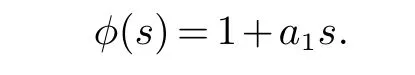
类似地,由2Δ3(φ-sφ′)8·h=0 的最高次项系数为零,得

则a1=0.因而,φ(s)≡1,即F 为黎曼度量.