基于CFD 的带附体KCS 船在波浪中的阻力及纵摇优化

李乐宇，吴建威，万德成*

1 上海交通大学 船海计算水动力学研究中心，上海 200240

2 上海交通大学 船舶海洋与建筑工程学院，上海 200240

3 武汉第二船舶设计研究所，湖北 武汉 430205

0 引 言

节能环保、安全舒适是进行船舶设计时需要考虑的2 个重要问题，而良好的阻力性能不仅可以有效提高主机有效功率，还能降低能源消耗，且在波浪中运动的船体，其耐波性的好坏将直接关系到船体的安全性与舒适性。当前，多数船舶的性能优化工作是基于改变船体全局或局部型线来完成的，涉及船体附体优化的工作相对较少，而通过为船体添加附体，如减摇鳍和压浪板，则可有效降低船舶阻力，提高主机功率并优化其耐波性。因此，有关船舶附体的优化工作具有一定的研究价值。

在基于船体型线变形实现船型优化方面，万德成等[1]针对船型优化的常用变形方法进行了详细归纳，并对每种变形方法进行了介绍。蔡寒冰等[2]利用径向基函数差值方法，通过优化船体艏部型线，完成了对DTMB 5415 船体的静水阻力优化。Miao 等[3]利用自由变形技术（free-form deformation，FFD）变形方法，针对片体为S60 的双体船，完成了多航速下的静水阻力优化。冯佰威等[4]通过改变DTMB 5415 船球鼻艏型线，利用势流及黏流计算方法，计算并优化了多航速下船体的静水阻力。Zong 等[5]运用self-blending 方法，采用少量控制变量完成了船体型线的变化，实现了船体总阻力的优化。

在通过为船舶添加附体来优化船体性能方面，Liu 等[6]运用实验方法为DTMB 5415 船舶艏部加装一个梭形附体，有效改善了船体在高雷诺数下的兴波状况，降低了船体艏部兴波高度，进而通过减小船体兴波阻力降低了船体总阻力，且降幅达8%。Wang 等[7]运用CFD 方法对不同工况下在船体艉部添加艉部襟翼的双体船的阻力、纵摇及垂荡进行了计算，最终双体船在添加艉部襟翼后其阻力、纵摇及垂荡均得到了一定程度的优化。对于存在多种附体的自主式水下航行器（AUV），附体的排布位置将会对其航行性能产生巨大影响，为此，Wang 等[8]通过改变AUV 附体的排布位置，完成了AUV 的水动力性能优化。陆超等[9]通过对船体球鼻艏（特殊附体）型线的变形，完成了船体性能优化。Zhang 等[10]通过优化船体型线，优化了船体的阻力性能。

目前，关于水面舰艇的优化计算分析工作多为静水阻力优化，与波浪中船舶减阻及耐波性优化相关的工作相对较少。然而，船舶通常在波浪中运动，不可避免地需要考虑波浪中船体的水动力性能优化工作，因此，有必要对波浪中船体进行阻力及耐波性的优化与分析。为此，本文将以KCS 船为研究对象，通过为船体添加减摇鳍和压浪板，并对附体主尺度进行优化来完成对船体总阻力及纵摇幅值的优化。计算工况为迎浪规则波，在此工况下，流体运动具有较强的非线性，为保证计算结果的准确性，计算采用黏流求解器naoe-FOAM-SJTU。。

1 计算工况选取

在 计 算 工 况 下，KCS 船 模 在Fr= 0.260 下 的航速为2.17 m/s。船模参数如表1 所示。

表1 KCS 船模主要参数Table 1 Main parameters of the KCS model

由相关实验数据[11]，可换算得到各工况下船舶重心处的垂荡幅值及船体纵摇幅值，如表2 所示。表中，工况Case 1～Case 5 分别为船体在不同波高、波长下一阶Stokes 深水波中的迎浪航行工况，图1 所示为依据实验结果绘制的图形。

考虑到迎浪下入射规则波的波长船长比（λ/L）在接近于1 时船舶容易产生近似“共振”的现象，使船舶在波浪中的无因次化运动幅值相对较大。由图1 及表2 可知，Case 3 工况下的船体无因次运动幅值较为剧烈，因此，本文的优化工况选取较为危险的Case 3 工况。

图1 垂荡与纵摇的流体动力学实验结果Fig. 1 Experimental fluid dynamics results of heave and pitch

表2 各工况下船体垂荡及纵摇幅值Table 2 Magnitude of heave and pitch in different cases

2 CFD 计算验证

CFD 计算采用的模型尺度船体参数如下：Lpp= 6.070 2 m，Lwl= 6.135 7 m，航速为2.17 m/s。依据实验，仅放开船体的纵摇及垂荡运动。计算采用半域计算，计算域范围如图2 所示。不同于惯用船体坐标系，本文计算域坐标系以主船体艏柱与设计水线面的交点作为坐标原点o，船艉指向x轴为正，y轴指向船体右舷为正，z轴垂直于xoy平面指向上方为正（后记作计算域坐标系）。计 算 域 选 取 范 围 如 下：-Lwl＜x＜3.0Lwl，0＜y＜1.5Lwl，-Lwl＜z＜0.5Lwl。

图2 船体计算域Fig. 2 Computational domain of hull

计算网格如图3 所示。由于船体处于迎浪航行状态，在确保计算结果准确性的前提下，为了尽量降低计算成本，仅着重对船艉前部的计算域进行了网格加密以降低波浪衰减；船艉后部的网格则逐渐稀疏，并通过在计算域后方设置消波区实现数值消波。

图3 CFD 计算网格划分Fig. 3 Grid division of CFD calculation

采用课题组自主研发的naoe-FOAM-SJTU 求解器对船体进行水动力性能计算，该求解器是基于开源代码CFD 工具箱OpenFOAM 开发的专门面向船舶与海洋工程水动力学问题的求解器。求解器以两相流不可压缩RANS 方程为控制方程，采用可以处理任意多面结构网格的有限体积法（FVM）离散控制方程，并结合界面压缩技术的流体体积（VOF）法捕捉自由面，然后采用SSTk-ω等湍流模型，再使用PISO（pressure-implicit with splitting of operators）方 法 处 理 速 度 和 压 力 的 耦合。本文中的网格由OpenFOAM 提供的网格生成工具snappyHexMesh 生成，网格生成方法是先生成均匀的笛卡尔坐标系下的背景网格，再通过将均匀网格分割成六面体单元来得到最后所需的网格。造波方式采用速度入口输入式造波，海绵层消波。计算得到在一个遭遇周期（Te）内船体总阻力系数Ct、纵摇幅值（船体纵摇运动的旋转重心为船体重心，记船体艏倾对应的纵倾角为负值，艉倾对应的纵倾角为正值）、船体重心处垂荡运动幅值，并与实验结果进行对比验证，如图4 所示。图中3 组船体的性能曲线均是以船体最大艉倾状态为起始时刻。依据实验数据[11]，将CFD 计算结果与实验流体动力学（EFD）结果进行对比并将数据进行无量纲化处理（图4）。图中：θ 为船体纵摇角；ζs为波幅；z为船体重心相对正浮状态的垂荡幅值；t/Te为船体运动稳定后一个遭遇周期内的时刻，当t/Te= 0 时船体处于最大艉倾时刻，当t/Te= 0.5 时船体处于最大艏倾时刻。

图4 CFD 计算结果与实验结果对比Fig. 4 Comparison between the numerical and experimental results

实验数据仅提供了总阻力系数Ct在一个遭遇周期内的平均值，故此处将CFD 计算所得总阻力系数作了平均处理并与实验结果的平均值进行对比，如表3 所示。由表可知，CFD 数值计算所得总阻力系数的平均值与实验值的误差为3.67%，小于5%，说明在一个遭遇周期内平均总阻力计算结果与实验结果吻合较好；船体纵摇幅值，也即船体在一个遭遇周期内运动过程中的最大艉倾角与最大艏倾角之差，由表3 及图4（b）可知，船体纵摇幅值的计算结果与实验结果吻合良好；船体垂荡幅值的计算结果与实验结果的误差为1.00%，结合图4（c），可知船体纵摇运动可通过CFD 计算得到较为精准的结果。

表3 CFD 计算值与实验值对比Table 3 Result comparison between CFD and EFD

图5 和图6 所示分别为船体在一个遭遇周期内以Te/4 为间隔的运动及兴波。为了便于分析船体运动，在图5 所示的静水自由液面与船体中纵剖面作了一交线（图中黑色直线），并将其作为观测船体运动状态的参考线。自由液面高度的量取依据计算域坐标系，记船体正浮时其设计水线处的自由液面高度为z= 0 m。

图5 一个遭遇周期内的船体运动Fig. 5 Hull motion in an encounter period

图6 一个遭遇周期内的船体兴波Fig. 6 Wave-making of hull in an encounter period

由船体运动及其兴波可知，船体艏部的纵摇幅值较艉部剧烈，有明显的球鼻艏出水及甲板上浪现象；在波浪中，船艏在达到最大纵倾角时会有砰击上浪现象，且船尾始终有较为剧烈的兴波。

3 附体对船体耐波性能的影响分析

由KCS 船的数值计算可知，船体艏部的运动幅度较为剧烈，尾部有较剧烈的兴波；船体运动幅度越大，船体兴波越剧烈，船体阻力也会随之增大；而降低船体运动幅值，优化船体兴波可以在一定程度上降低船体阻力，减小主机功率的损失。

在迎浪条件下船舶运动主要是纵摇和垂荡。本文从优化船体纵摇的角度出发，尝试在船体艏部加装一对板状结构的降低纵摇运动的装置—减摇鳍，探讨在船体运动中减摇鳍与水体相互作用是否可在一定程度上优化船体的纵摇幅值；同时，因船体尾部兴波较为剧烈，可考虑在船体艉部加装压浪板，以优化船体尾部的兴波。

附体添加位置及其各自的形状如图7 所示。其中，a 为原始船体，b 为添加2 种附体后的船体；左下图展示的是减摇鳍的俯视图与主视图，右下图展示的是压浪板的俯视图与主视图。考虑到船体艏部在纵摇过程中运动幅值较大且型线收缩较为剧烈，添加减摇鳍不会对船体最大型宽产生明显影响，故将减摇鳍添加于船体艏部。依据计算域坐标系，减摇鳍最前端边缘的坐标为z= 0.003Lwl，x= 0.028Lwl，其中部厚度为0.004Lwl；压浪板底面与船体艉封板交接处的高度为z= 0.005Lwl。减摇鳍与压浪板和设计水线的交角均为2°。

为了保证添加的附体不会给船体水动力性能带来负面影响，计未添加附体的KCS 船体为船Org，并对船A（仅添加减摇鳍）、船B（仅添加压浪板）、船C（同时添加减摇鳍和压浪板）这3 艘KCS 船分别进行计算，分析其各自在一个遭遇周期内的总阻力平均值及纵摇幅值。通过计算，可得船Org 以及船A、船B、船C 的水动力性能如表4 所示。表中，船体总阻力Rt由摩擦阻力Rf与剩余阻力（压阻力）Rr构成，Rr则由兴波阻力Rw与粘压阻力Rpv构成。

由表4 的数据对比，可知：添加附体对船体总阻力和纵摇均有一定的优化效果；船A 与船B 相比，单独添加减摇鳍的阻力优化效果要优于单独添加压浪板的船体；添加了减摇鳍与压浪板的船C的水动力性能优于单独附体作用下的船体性能。结合阻力成分的数值结果，还可知在附体作用下，船体的压阻力有较为明显的改善，而摩擦阻力则没有明显的优化效果，甚至还会略增大。当为船体同时添加减摇鳍与压浪板（船C）时，船体的总阻力、纵摇幅值均得到了一定程度的优化，其剩余阻力较裸船体降低了18.43%，而船体湿表面积因添加的附体增大，导致其摩擦阻力较裸船体又增大了0.303%。

图8 展示了模型尺度下，船A 与船Org 在一个遭遇周期内不同时刻减摇鳍后方时不同横截面的涡量对比。由图可知，减摇鳍对水体的扰动导致在减摇鳍附近产生了涡量，在船体前进过程中，涡量向船体后方传播。图中，t1时刻为船体最大艉倾时刻，t3时刻为船体最大艏倾时刻。由图可以看出，减摇鳍的存在使得船体的运动幅度减小，船体的纵摇运动得到了改善。

图8 船A 与船Org 的涡量分布对比Fig. 8 Comparison of vorticity magnitude between ship A and ship Org

船体在纵摇过程中，其减摇鳍将随船体艏部不断做“出水-入水”的往复运动。在船体艏倾过程（t2～t3）中，船体处于由正浮状态至艏倾的运动过程中，此时减摇鳍入水运动，船体受到垂直于减摇鳍运动方向的向上的力；船体在由艏倾恢复正浮状态（t3～t4），并由正浮至艉倾（t4～t1）的过程中，此时减摇鳍出水运动，船体受到垂直于减摇鳍运动方向的向下的力。减摇鳍受到的力在船体运动过程中一定程度上会增加船体的运动阻尼，进而降低船体运动的纵摇幅值。

由图9 可见，在艏部加装了减摇鳍的船体较原始船在船舯附近的兴波幅值得到了改善，船体减摇鳍后方的兴波幅值较裸船体尺度减小。

图9 船A 与船Org 的船体兴波对比Fig. 9 Comparison of hull wave-making between ship A and ship Org

添加减摇鳍后，船体在最大艉倾、艏倾状态下的船体压力分布如图10 中t1，t3时刻所示：相对于船Org，船A 在t1时刻时，船体底部中前方的高压范围减小，艉部低压范围减小；在t3时刻，船体底部最低压力绝对值减小，船体底部压力分布得到了一定程度的改善。然而，因减摇鳍对水体的扰动导致涡的产生，改变了流场的均匀性，使得减摇鳍后方船体表面局部区域的压力分布发生了突变。

图10 船A 与船Org 船体压力分布对比Fig. 10 Comparison of pressure distribution between ship A and ship Org

图11 对比了船B 与船Org 在同一遭遇周期内不同时刻的尾部兴波。对于未加装压浪板的船Org，其尾部存在较为剧烈的尾部兴波；加装压浪板（船B）后，当船尾部产生波峰时，尾部兴波在遇到压浪板后会被压浪板阻断，从而致使尾部兴波幅值明显降低。同时，由于尾部流体对压浪板的冲击，当压浪板受到垂直板面向上的压力，尤其是当船尾经历波峰时，船体正处于由艏倾恢复正浮的过程，此时艉部受力的增加产生的力矩可以降低船体扶正的加速度；当尾部经历波谷时，船体处于正浮至艉倾过程，该压力的存在一定程度上会增加船体的运动阻尼，进而降低船体的纵摇幅值。

图11 压浪板引起船体兴波变化对比Fig. 11 Comparison of wave-making variation caused by stern flap

由图12 可看出，添加压浪板后，对于船体底部，其在最大艏倾时刻船艏部分的高压区范围减小，在最大艉倾时刻船艉部分的低压区范围减小；而船体侧面由于不存在减摇鳍对水的扰动，其阻力分布和船Org 相比无明显差异。

图12 压浪板引起的船体压力分布变化对比Fig. 12 Comparison of pressure distribution variation caused by stern flap

4 附体主尺度优化及结果分析

考虑通过改变附体尺度来优化船体兴波。对于减摇鳍，通过增大宽度来增加其与水体的接触面积，以此提供更大的减摇力矩，从而提升减摇效果；对于压浪板，由图11 可看出，其已经具有一定的艉部压浪效果，可考虑适当减小长度。附体的变形范围如表5 所示。表中：“变形范围”指附体变形后尺度与初始附体变形尺度的比值；α 为变形后减摇鳍宽度与初始减摇鳍宽度的比值，其取值范围不可使减摇鳍外边线超出船体型宽；β 为变形后压浪板长度与初始压浪板长度的比值，为减小压浪板对船体总长的改变量，需控制参数β 的取值范围以使压浪板长度在1/40～1/25倍船体总长范围内变化。

表5 附体变形范围取值Table 5 Variable range of appendages

在变形范围内选取30 个样本点，生成30 艘不同附体尺度的样本船（附体变形采用FFD 方法），样本点的选取方案如图13 所示。经计算，各样本船在一个遭遇周期内的阻力及纵摇幅值如表6 所示。

表6 各样本船的阻力及纵摇幅值Table 6 Resistance and pitch magnitude of each sample ship

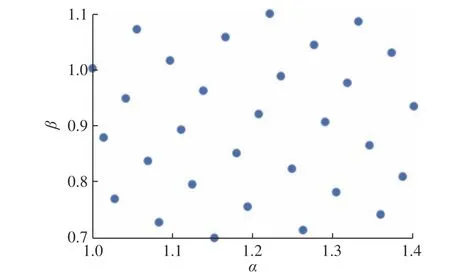
图13 30 组变量分布Fig. 13 Distribution of 30 groups of variables

由表6 中数据建立Kriging 模型，依据该模型经优化算法得到以纵摇幅值及总阻力为目标的Pareto 前沿，如图14 所示。图中，f1为阻力对应的目标函数，f2为纵摇幅值对应的目标函数。

图14 Pareto 前沿Fig. 14 Pareto front line

从中选取3 种优化后的附体形式，并将其分别安装于KCS 船上。将加装了3 种附体的KCS 船分别记为Hull 1，Hull 2 和Hull 3，其各自的附体相对原始附体的变形量如表7 所示。由这3 艘样本船在Pareto 前沿的分布位置，可了解到Hull 1 的 纵 摇 幅 值 最 优，Hull 3 的 阻 力 性 能 最 优，而Hull 2 的纵摇幅值与阻力性能优化程度介于两者之间。为了验证Pareto 前沿的准确性，对Hull 1，Hull 2，Hull 3 分别进行数值计算，得到了其阻力及纵摇幅值，并与Pareto 前沿拟合所得Hull 1，Hull 2，Hull 3 的阻力（数值拟合阻力）和纵摇（数值拟合纵摇）进行了对比验证，结果如表8 所示。

表7 3 艘样本船对应的形变量Table 7 The corresponding variables of three sample ships

表8 样本船的阻力及纵摇幅值验证结果Table 8 Validation of resistance and pitch magnitude of sample ships

表9 对比了3 艘优化样本船与船Org 的船体性能。

由表9 可知，加装附体后，3 艘优化样本船的船体阻力及纵摇均得到了一定程度的优化。以Hull 1为例，计算得到其与船Org 的压力分布如图15 所示。由图可看出，在计算域坐标系下的船体艉倾最大时刻t1，Hull 1 艉部收缩段的压力较船Org有所增大，艉部压力在x轴正方向（由船艏指向船艉，与船体航向相反）的分力减小，其底部中前部分的压力较船Org 有所减小，因船体处于艉倾状态，该区域的压力在x轴正方向的分力较船Org 的小，致使船体压力在x轴正方向的分力减小，船体压阻力降低；船体在由艉倾至艏倾的中间时刻t2，相较船Org，Hull 1 的压力分布变化主要体现在压浪板受到压力和艏部减摇鳍引起的压力突变方面；船体在最大艏倾时刻，Hull 1 底部中前方的压力相较船Org 有所增大，艉部高压区的范围扩大至压浪板，从而使得船体压力在x正方向的分力减小，船体压阻力降低；船体在由艏倾至艉倾的中间时刻t4，其艉部收缩段的压力增大，且艏肩前部相较船Org 出现了低压区域，致使船体压力在x正方向减小，船体压阻力降低。

图15 Hull 1 与船Org 的压力分布对比Fig. 15 Comparison of pressure distribution between Hull 1 and ship Org

表9 样本船与原始船Org 的性能对比Table 9 Comparison of hydrodynamic performance between sample ships and ship Org

综上分析，可知添加附体后船体压阻力在一个遭遇周期内多数时刻是优于船Org 的。

图16 展示的是船Org 与Hull 1 的船体兴波对比，图17 展示的是各时刻下半船船体艉部后方横剖面x/Lwl= 1.1 处两船体兴波横剖线对比（坐标系采用计算域坐标：xoy为船体正浮时设计水线所在平面，xoz为船体中纵剖面所在平面）。

图17 x/Lwl = 1.1 处Hull 1 与船Org 的兴波对比Fig. 17 Comparison of wave-making between Hull 1 and ship Org at x/Lwl = 1.1

结合图16 可以看出，在t1时刻，船体艉部经历波谷，对于船Org，在船体艉部的作用下，自由液面被抬升，从而产生了“波谷中的波峰”（以下称“波峰”），而Hull 1 则因受到艉部压浪板的影响，压浪板后方的“波峰”在0≤y＜0.1 范围内较船Org 的高度更大，但在0.1≤y＜0.43 范围内，船体尾部后方“波峰”的高度却被降低了。在t2时刻，船体艉部处于峰谷交界处，在0.06≤y＜0.23 范围 内，Hull 1 尾 部 兴 波 的 波 高 较 船Org 的 大；在0≤y＜0.06，0.23≤y＜0.50 范围内，Hull 1 尾部兴波的波高较船Org 的小。在t3，t4时刻，Hull 1 尾部兴波的波高小于船Org。

图 16 Hull 1 与船Org 的兴波对比Fig. 16 Comparision of wave-making between Hull 1 and ship Org

图18 展示的是不同时刻下，纵剖面y/B=1（B为船体最大宽度）处船Org 与Hull 1 的兴波对比。图中坐标系采用的是计算域坐标系，船体设计水线于xoz平面投影为线段0≤x≤6.1357。

图18 y/B=1 处Hull 1 与船Org 的兴波对比Fig. 18 Comparison of wave-making between Hull 1 and ship Org at y/B=1

结合图16 可以看出，在t1时刻，船体中前部经历波峰，此时Hull 1 兴波的最大波峰峰值小于船Org，船体艉部经历波谷，在船艉后方7≤x＜8处，Hull 1 兴波的最大波谷峰值小于船Org；在t2时刻及3≤x＜4 范围内，Hull 1 兴波的最大波峰峰值小于船Org，在1≤x＜2 及7≤x＜9 范围内，Hull 1兴波的最大波谷峰值小于船Org；在t3时刻及6≤x＜7.5 范围内，Hull 1 兴波的最大波峰峰值小于船Org，在2≤x＜3 及7.5≤x＜8 范围内，Hull 1 兴波的最大波谷峰值小于船Org；在t4时刻及6≤x＜7.3，8.2≤x＜9 范围内，Hull 1 兴波的最大波峰峰值小于船Org，在4≤x＜5 及7.3≤x＜8.2 范围内，Hull 1 兴波的最大波谷峰值小于船Org。

依据Hull 1 与船Org 在横、纵切面的兴波对比，并结合图16，可知在减摇鳍和压浪板的作用下，Hull 1 的兴波较船Org 有所缓和。

结合表6 所示的附体变形参数，考虑到Hull 1与Hull 2 的减摇鳍尺度较为接近，Hull 2 与Hull 3的压浪板尺度较为接近，为了探究附体尺度对流场的影响，选择Hull 2 与Hull 3 来比较减摇鳍后方的涡量变化，选择Hull 1 与Hull 2 来比较压浪板对船体尾部兴波的影响。

减摇鳍与水相互作用生成的涡会沿船长方向向后传递，将Hull 2 与Hull 3 减摇鳍后方x/Lwl=0.144横剖面处的涡量进行了对比，如图19 所示。选取船体由正浮状态向到最大艏倾状态运动的中间时刻（t=nTe+1/8Te）和由正浮状态向到最大艉倾状态运动的中间时刻（t=nTe+7/8Te）其截面处的涡量进行对比。

图19 Hull 2 与Hull 3 涡量对比Fig. 19 Comparison of vorticity magnitude between Hull 2 and Hull 3

由图19 可知，在2 个时刻下，由于Hull 3 的减摇鳍尺度稍大，对水体的扰动相对较大，故其减摇鳍后方的涡量范围也较Hull 2 稍大。

为 便 于 观 察Hull 1 与Hull 2 尾 部 兴 波 的 差异，在船体运动的一个遭遇周期内，选取部分船艉经历波谷的时刻进行了对比观察，结果如图20所示。由图20 (a)和图20 (b)所示时刻的船体尾部兴波对比，可知Hull 2 压浪板的压浪效果要优于Hull 1，说明较长艉部压浪板的压浪效果更好。

图20 Hull 1 与Hull 2 的尾部兴波对比Fig. 20 Comparison of wave-making between Hull 1 and Hull 2

5 结 语

对于迎浪航行的KCS 船，其船艏的运动幅值较为剧烈，会出现轻微的甲板上浪以及球鼻艏部分出水现象。本文通过为KCS 船体添加减摇鳍和压浪板，并改变附体主尺度，同时结合优化算法，实现了船体在一个遭遇周期内的总阻力平均值及纵摇幅值的优化。

为船体添加附体，并对附体主尺度进行优化后，所得优化船体在一个遭遇周期内的大多数时刻其压力峰值都较裸船体有所减小，船体的压力分布会发生变化，导致船体压阻力降低了近17%；由于船体附体会导致船体湿表面积增大，使得船体摩擦阻力相对裸船体有小于0.5%的增大，船体总阻力约有10%的降低。表明附体的存在，使得船体在运动过程中受到的阻尼增大，船体纵摇运动得到改善，纵摇幅值约减小12%。因此，为KCS 船体添加减摇鳍和压浪板可以有效改善其纵摇与总阻力。在后续工作中，还需探究压浪板、减摇鳍位置的选取对船体水动力性能的影响，以及附体结构强度的可靠性。