基于Friendship的高速客船特征参数灵敏度分析
张守慧,谢玲玲,冯佰威,田中文
(1.中国船级社 海南分社,海南 海口 570206;2.武汉理工大学 高性能船舶技术教育部重点实验室,湖北 武汉 430063;3.中船黄埔文冲船舶有限公司,广东 广州 510715)
0 引 言
基于计算流体动力学(CFD)数值模拟的方法,通过CFD数值计算寻找最佳设计方案[1-6]。应用Friendship全参数化建模软件完成某高速客船全参数化模型的建立,对初始模型应用SHIPFLOW流体计算软件进行兴波阻力的计算,将结果与船模试验结果进行对比,以验证计算的可靠性。对所建的高速客船模型,根据设计经验选取艏部特征参数及其变化范围,然后通过Sobol算法使变量在设计空间生成均匀的设计方案,并利用SHIPFLOW对所生成的若干个设计方案进行兴波阻力计算,最后对计算结果进行分析,从而得出各特征参数的灵敏度大小。
1 船体型线全参数化建模和模型网格划分
应用Friendship软件完成某高速客船全参数化建模,应用SHIPFLOW软件中自带网格划分功能对模型进行网格划分,为后续特征参数灵敏度分析奠定基础,具体参见文献[7]。
2 特征参数灵敏度分析
数学模型在参数灵敏度分析中非常重要,通常数学模型有3个重要组成部分,即参数输入、变量输出及两者关系。参数输入具有随机性[8-9],因此输出变量具有不确定性,而研究这种不确定性及两者关系则构成数学模型的不确定性和灵敏度分析。
2.1 输入参数选取
根据该高速客船模型的几何特征和控制型线的特征参数,初步选择13个特征参数作为模型输入参数,并根据设计经验和实际情况进行多次试算,最终确定选择的特征参数变化范围,如表1所示。

表1 输入参数及其变化范围
2.2 输入参数与输出变量的关联
在搜索过程中,输入参数取值的变化会导致船体型线发生变化,船舶的水动力性能也会发生相应的变化。由于所建的客船模型是高速船舶,因此在优化过程中选择船体艏部进行兴波阻力优化,在兴波阻力优化的过程中需要保证船舶满足一定的营运性能,同时优化后的船型具有足够的浮力保证船舶浮态不会发生较大变化。在静水力计算结果中,模型的排水量和浮心纵向位置均满足误差要求,因此在灵敏度计算过程中,将排水量和浮心纵向位置作为约束条件,使优化后的船舶排水体积和浮心纵向位置比优化前的误差更小,可保证其误差在允许的范围之内。
2.3 Sobol算法计算结果分析
采用Friendship中的Sobol模块,选用Sobol搜索算法,对选择的设计变量上下限和兴波阻力系数选取初始的200组方案,航速则选取设计航速18 kn。经过长时间的计算分析,最终得到输出变量兴波阻力的计算结果。
2.3.1 设计变量在约束空间的分布
各设计变量在约束空间的分布如图1~图13所示。通过分析各设计方案在整个设计空间的分布,选取的13个艏部特征参数在设计空间中均为均匀分布,因此采用Sobol算法可对整个设计空间进行较为精确的估计,为后续优化提供合适的空间。
图1 cpcTanAtForeLpp在约束空间的分布

图2 cpcFullness2在约束空间的分布
图3 tanCpcFullness2在约束空间的分布

图4 tanCpcTanAtForeBase在约束空间的分布
图5 tanCpcYAtForeBase在约束空间的分布

图6 wlFullness在约束空间的分布
图7 wlTanAtForeLpp在约束空间的分布

图8 tanWLTanAtForeLpp在约束空间的分布

图9 tanWLYAtForeLpp在约束空间的分布

图10 tanWLFullness2在约束空间的分布

图11 fullLowTanAtForeLpp在约束空间的分布

图12 fullLowYAtForeLpp在约束空间的分布
图13 fullLowFullness2在约束空间的分布
2.3.2 设计变量对兴波阻力的影响趋势
各设计变量对兴波阻力的影响趋势如图14~图26所示,各图中的曲线和直线分别代表二次函数线和一次函数线。通过分析这两条数据线可判断特征参数对兴波阻力影响因子的大小,其中曲率平缓表示影响因子较小,曲率陡峭表示影响因子较大。

图14 cpcTanAtForeLpp对兴波阻力的影响趋势
由图14、图15、图16、图18、图20、图21、图24和图26可知:曲线和直线有一定的弧度相交,说明选取的特征参数cpcTanAtForeLpp、cpcFullness2、tanCpcFullnes2、tanCpcYAtForeBase、wlTanAtForeLpp、 tanWLTanAtForeLpp、fullLowTanAtForeLpp和fullLowFullness2对兴波阻力的影响因子较大。分析各图中的二次函数曲线和一次函数直线:cpcTanAtForeLpp数值取45.825~50.200,可获取特征参数cpcTanAtForeLpp对兴波阻力影响的最小值,在后期船型优化中,cpcTanAtForeLpp的上下限分别取45.825和50.200;CpcFullnes2数值取0.255~0.276,可获取特征参数CpcFullnes2对兴波阻力影响的最小值,在后期船型优化中,CpcFullnes2的上下限分别取0.255和0.276;tanCpcFullnes2数值取0.200~1.200,可获取特征参数tanCpcFullnes2对兴波阻力影响的最小值,在后期船型优化中,tanCpcFullnes2的上下限分别取0.200和1.200;tanCpcYAtForeBase数值取5.400~10.105,可获取特征参数tanCpcYAtForeBase对兴波阻力影响的最小值,在后期船型优化中,tanCpcYAtForeBase的上下限分别取5.400和10.105;wlTanAtForeLpp数值取-15.521~-13.000,可获取特征参数wlTanAtForeLpp对兴波阻力影响的最小值,在后期船型优化中,wlTanAtForeLpp的上下限分别取-15.521和-13.000;tanWLTanAtForeLpp数值取-45.000~20.000,可获取特征参数tanWLTanAtForeLpp对兴波阻力影响的最小值,在后期船型优化中,tanWLTanAtForeLpp的上下限分别取-45.000和20.000;fullLowTanAtForeLpp数值取-4.025~-3.000,可获取特征参数fullLowTanAtForeLpp对兴波阻力影响的最小值,在后期船型优化中,fullLowTanAtForeLpp的上下限分别取-4.025和-3.000;fullLowFullness2数值取0.400~0.500,可获取特征参数fullLowFullness2对兴波阻力影响的最小值,在后期船型优化中,fullLowFullness2的上下限分别取0.400和0.500。

图15 cpcFullness2对兴波阻力的影响趋势

图16 tanCpcFullnes2对兴波阻力的影响趋势

图17 tanCpcTanAtForeBase对兴波阻力的影响趋势
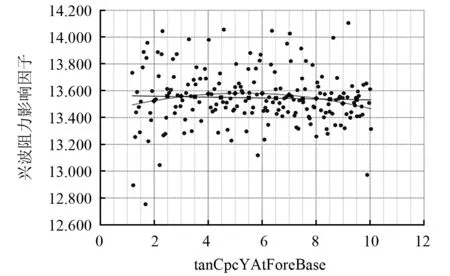
图18 tanCpcYAtForeBase对兴波阻力的影响趋势

图19 wlFullness对兴波阻力的影响趋势

图20 wlTanAtForeLpp对兴波阻力的影响趋势
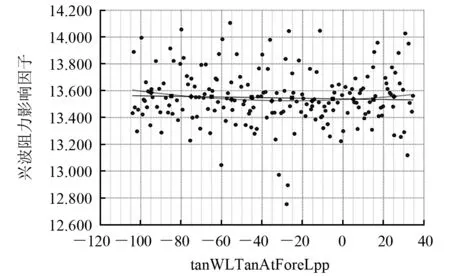
图21 tanWLTanAtForeLpp对兴波阻力的影响趋势

图22 tanWLYAtForeLpp对兴波阻力的影响趋势
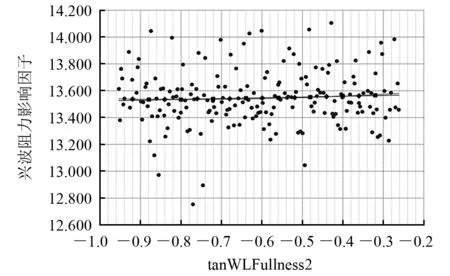
图23 tanWLFullness2对兴波阻力的影响趋势
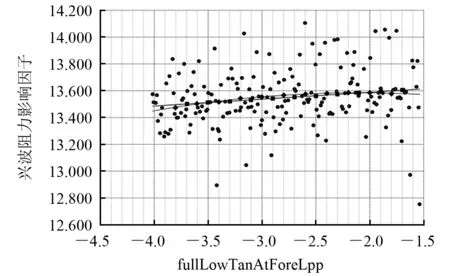
图24 fullLowTanAtForeLpp对兴波阻力的影响趋势

图25 fullLowYAtForeLpp对兴波阻力的影响趋势

图26 fullLowFullness2对兴波阻力的影响趋势
由图17、图19、图22、图23和图25可知:各图中的二次函数曲线和一次函数直线接近重合,说明选取的特征参数tanCpcTanAtForeBase、wlFullness、tanWLYAtForeLpp、tanWLFullness2和fullLowYAtForeLpp对兴波阻力的影响因子较小,在后期船型优化中可不考虑这些特征参数。
经过对上述Sobol算法灵敏度计算结果分析,可将兴波阻力影响较小的特征参数剔除,留下对兴波阻力影响因子较大的特征参数及其最佳数值取值范围,并以此作为后续船型优化的设计变量,具体参见文献[7]。
3 结 语
在特征参数上下值变化范围选取上采用经验选取,缺乏精度,在后续优化过程中由于特征参数上下值变化范围的误差可能对最优船型兴波阻力的数值和船体形状的变化误差产生一定影响,因此如何减小特征参数上下变化值选取上的误差,提高其精度,是未来需要进一步研究的问题。
——以某铅锌矿为例

