基于传递矩阵法的纵肋圆柱壳振动特性计算

田 杨，章桥新，余金桂，黄 涛

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北工业大学 土木建筑与环境学院，湖北 武汉 430068)

0 引 言

圆柱壳结构被广泛运用于建筑、航空航天和船舶等领域，加肋圆柱壳更是潜艇的主要结构形式。李学斌[1]利用波动法讨论圆柱壳在不同的边界条件下固有频率和模态振型的计算精度，结果表明，当波动法运用在两端简支的细长圆柱壳时，精度较高。江晨半等[2]基于精细积分和传递矩阵法对变厚度圆柱壳进行振动分析，与有限元仿真结果进行比较验证准确性，并讨论边界条件和结构尺寸对振动特性的影响。何伟东等[3]基于虚拟质量法和边界元法研究水下有限长圆柱壳的声辐射，分析不同深度的辐射声压值。何春雨等[4]利用有限元法通过数值仿真研究海水管路系统的振动特性。

传递矩阵法是一种分析链式结构的常用方法，其优点是计算过程清晰明了，方法简便，结果精度高，只需将结构写成一阶微分方程形式即可使用传递矩阵法。国外较早使用传递矩阵法计算圆柱壳振动特性的是日本学者IRIE等[5]，除研究双层圆柱壳外，还研究变厚度圆锥壳[6]等，但在求解结果时采用幂级数展开取逼近，导致结果精度不高。张娟等[7]基于传递矩阵法研究渔船推进轴系的振动特性。向宇[8]运用微分方程和矩阵理论推导传递矩阵的精确形式。王祖华等[9]使用传递矩阵的精确形式求解短粗环肋圆柱壳的振动特性，但在考虑环肋与壳体的相互作用时，忽略面外弯曲和扭转振动。

基于传递矩阵法计算纵肋圆柱壳的振动特性，按照传递方向将传递矩阵法分为周向传递矩阵法和轴向传递矩阵法。在考虑环肋与壳体相互作用时将面内和面外作用力全部加上，推导纵肋圆柱壳的场传递矩阵和点传递矩阵，采用精细时程积分法求解，保证计算过程的精度，并讨论两种传递矩阵法适用条件及范围。

1 基本理论公式

基于Flugge壳体理论，壳体的应力和应变的等式按照位移的形式，内力和内力矩可表达为

(1)

式中：Nx和Nθ分别为面内的轴向力和周向力；Nxθ和Nθx分别为不同方向的剪切力；Mx和Mθ分别为绕周向和轴向的弯矩；Mxθ和Mθx分别为不同方向的扭矩；K为弯曲刚度，K=Eh/(1-μ2)，其中，E为弹性模量，h为厚度，μ为泊松比；D为薄膜刚度，D=Eh3/12(1-μ2)；u为轴向位移；x为轴向长度；v为周向位移；R为半径；θ为周向角；w为径向位移；Qx为横向剪力。

径向位移与转角ψ之间的关系为

(2)

柱坐标系的圆柱壳段在自由振动时由惯性力引起的分布载荷为

(3)

式中：px、pθ和pr分别为轴向、周向和径向的惯性力，其中x、θ和r分别为圆柱壳的轴向、周向和径向；ρ为材料密度；t为时间；ω为自由振动频率；时间因子省略。

圆柱壳的振动微分控制方程表示为

(4)

2 纵肋圆柱壳自由振动特性分析

图1为纵肋圆柱壳结构示例。图1中，壳体长为L，半径为R，且该圆柱壳满足壳体理论中的基本假设。

图1 纵肋圆柱壳结构示例

2.1 基于周向传递的场传递矩阵

周向传递矩阵法与轴向传递矩阵法最大的区别在于状态矢量元素传递的方向不同，当需要状态矢量元素沿周向传递时，壳体位移分量和内力展开成三角函数形式与轴向时有所不同，对于圆柱壳边界条件为两端简支、壳体自由振动时，壳体位移分量和内力可以写成如下形式：

(5)

式中：m为轴向半波数；标有上划线的量为无量纲变量；Qθ为周向剪力；Sθ为Kelvin-Kirchhoff剪力。

为了方便计算，同样引入如下无量纲参数：

(6)

式中：l和H分别为长度和厚度对应的无量纲参数；λ为频率因子。

在16个状态矢量元素中只保留8个，消去Qx、Q、N、Nθ、Mx和Mxθ，柱壳振动方程可写成矩阵微分方程：

(7)

式中：SYM表示对称矩阵。

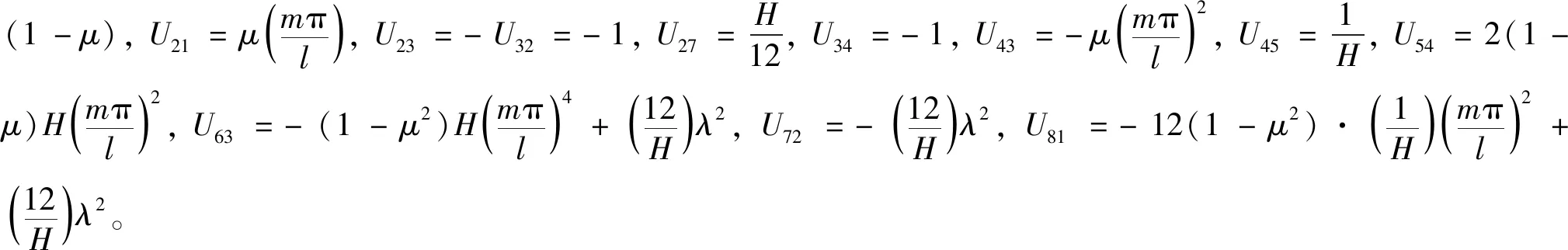
(8)

解该微分方程的精度决定最终解的精度，为了得到高精度的结果，采用精细时程积分法计算。

2.2 纵肋处点传递矩阵

纵肋的存在会改变肋骨与圆柱壳连接处的状态向量。肋骨对圆柱壳的作用力主要表现为法向力、切向力、纵向力及纵向力绕轴线的弯矩。将这些作用力充分考虑后得到的纵肋运动微分方程[10]为

(9)

利用圆柱壳在纵肋骨处的连续条件和平衡条件，并将位移和内力沿轴向模态展开，整理后可写成如下矩阵方程：

(10)

3 数值算例及讨论

按传递方向将场传递矩阵和点传递矩阵依次相乘，结合边界条件得到频率方程，采用精细时程积分法计算，通过MATLAB软件编程计算得到圆柱壳的固有频率，将固有频率代入传递矩阵，利用各截面状态向量非零元素的相对比值得到振动模态。通过算例1验证方法的正确性，将周向传递矩阵法与ANSYS仿真值进行对比分析。算例2讨论周向传递矩阵法和轴向传递矩阵法在计算圆柱壳自由振动特性的使用范围。

(1)算例1。两端简支加外纵肋圆柱壳，圆柱壳体总长L为1.000 m，半径R为0.500 m，壳体厚度h为0.010 m，肋骨截面尺寸为0.020 m×0.020 m，在圆柱壳上一共添加4根纵肋，结构材料密度ρ为7 850 kg/m3，泊松比μ为0.3，弹性模量E=2.1×1011Pa。固有频率计算结果如表1所示，表1括号内的数字分别为该模态的周向波数n和轴向半波数m。模态振型如图2～图5所示。

由表1可知：推荐方法与ANSYS仿真结果对比，最大误差为1.68%，最小误差为0.01%，能满足实际工程要求。图2和图3比较2阶固有频率时的模态振型。图4和图5比较6阶固有频率时的模态振型。推荐方法计算的模态振型与ANSYS仿真结果的模态振型基本一致，验证方法的正确性。

图2 2阶(4，1)模态振型(传递矩阵法)

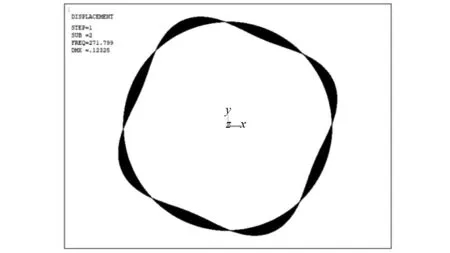
图3 2阶(4，1)模态振型(ANSYS)

图4 6阶(6，1)模态振型(传递矩阵法)

图5 6阶(6，1)模态振型(ANSYS)

表1 传递矩阵法与ANSYS频率计算结果对比 Hz

(2)算例2。两端简支不加肋圆柱壳。圆柱壳体总长L为0.200 m，半径R为0.100 m，壳体厚度h为0.002 m，结构材料密度ρ为7 850 kg/m3，泊松比μ为0.3，弹性模量E=2.1×1011Pa。按周向传递矩阵法计算得到的前10阶对称模态固有频率如表2所示。为作对比，表2给出ANSYS计算结果及该算例采用轴向传递矩阵法计算的结果。前10阶反对称模态固有频率与前10阶对称模态固有频率完全相同，不再单独列表显示。

表2 3种不同方法前10阶对称模态固有频率对比结果 Hz

由表2可知：在m取值较小(低频部分)时周向传递矩阵法计算结果与ANSYS吻合较好，而轴向传递矩阵法则在n取值较小(高频部分)时与ANSYS计算结果接近。2种方法在计算圆柱壳的自由振动特性时可以互为补充，即低频部分采用周向传递矩阵法，高频部分采用轴向传递矩阵法。

4 结 语

基于传递矩阵法，结合精细时程积分法，建立一种快速计算纵肋圆柱壳自由振动特性的周向传递矩阵法。在验证该方法的有效性上，讨论周向传递矩阵法和轴向传递矩阵法的适用范围和条件。结果表明，该方法与ANSYS解吻合较好，计算精度较高，且轴向传递矩阵法适用于圆柱壳高频部分的计算，周向传递矩阵法适用于圆柱壳低频部分的计算，由于只有两端简支边界圆柱壳在轴向位移函数才可以设为三角函数形式，因此周向传递矩阵法仅适用于简支边界。