掠叶片进口流场中周向不均匀性的影响

唐明智 ，金东海 ，2，郭 昕 ，桂幸民 ，2

（1.北京航空航天大学能源与动力工程学院，北京100191；2.先进航空发动机协同创新中心，北京100191；3.中国航发四川燃气涡轮研究院，成都610500）

0 引言

现阶段3D数值模拟在风扇/压气机设计中得到了广泛使用。然而在设计的初级阶段，通流模型由于一方面可以快速提供风扇/压气机的性能及内部流动特性，另一方面也易于将经验参数纳入到数值模拟中[1-2]，因此仍具有重要作用[3-4]。目前应用最广泛的通流方法是流线曲率法，而基于周向平均Euler[5]或Navier-Stokes（N-S）方程[6-8]的通流模型也同样被广泛研究，并应用于压气机的特性预测和流场模拟。这些通流模型适用于跨声压气机的流场模拟和性能预测[9]。

在对N-S方程进行周向平均的过程中，不可避免地产生一些附加项，其中与表面力相关的项被模化为无黏叶片力项和叶片黏性项，而对于由于流场的周向不均匀性及控制方程的非线性所引发的高阶项，即周向脉动应力项，早期研究认为其对流场的影响可以忽略，即假设叶片通道进口前流动参数沿周向均匀分布，这主要是由于在早期研究中，相对于控制方程中的其他项，反映周向不均匀性的项的量级很小；另一个原因则是设计者缺乏模型来预测这些项的值[10]。然而，随着当前压气机负荷的提高，以及弯掠叶片技术的广泛应用，周向不均匀性的影响正被逐步认识到，有助于更为精确地应用弯掠叶片技术。事实上，这些项的作用可能会比黏性项的作用更大，并且随着负荷的增大，其作用也会增强[11]。此外，周向不均匀性会影响流动参数的轴向和展向的分布[9，12-13]，并能反映角区失速和径向掺混等现象。对于掠叶片，叶片通道进口的流动平衡也会被周向不均匀性所影响，并会诱导流动参数的重新分配，而引发周向不均匀性的1个主要来源就是无黏叶片力[14]。

为了模化周向不均匀性，通常的方法是计算周向脉动应力项，其中1种方法是开展S1流面上的计算，然后提取出周向脉动应力项。吴仲华采用中心流线法来简化对S1流面的计算[15]，并在之后得到了一定的发展[16-17]。由于周向脉动应力项具有谐波特征[18]，因此非线性谐波平衡法也被用来模化周向不均匀性[19]，不过这种方法并未获得广泛应用。

文献[20]通过应力输运模型对周向脉动应力项进行建模，分析了具有不同掠角的掠叶栅在0°迎角下流场中周向不均匀性的影响，结果表明周向不均匀性会改变掠叶片进口流动参数，并引发进口新的径向平衡。本文在此基础上应用该应力输运模型分析迎角改变时掠叶栅进口流场中周向不均匀性的作用。

1 控制方程

1.1 周向平均通流模型

在相对柱坐标系中对N-S方程进行周向平均[10]，并将周向脉动应力项整合为周向脉动源项P，可得到通流模型的主控方程

方程中各项定义为

式中：U为守恒量；F和G为对流（无黏）通量；Fv和Gv为扩散（黏性）通量；S为N-S方程组在相对柱坐标下导出的源项；FB为无黏叶片力；FF为黏性叶片力。

定义由于叶片切向厚度产生的堵塞系数b

式中：Δφ=φs-φp，为叶片通道周向宽度；N为叶片数。

在叶片区b＜1，在非叶片区b=1。周向脉动源项P中的高阶项即为周向脉动应力项，这些项是由于叶轮机的周向不均匀性及N-S方程的非线性所导致的，其与周向脉动源项均能够反映周向不均匀性的大小。

与文献[20]类似，为分析叶片通道进口径向平衡的改变，对方程（1）中的径向动量方程进行推导及简化，可以得到无黏形式的完全径向平衡方程

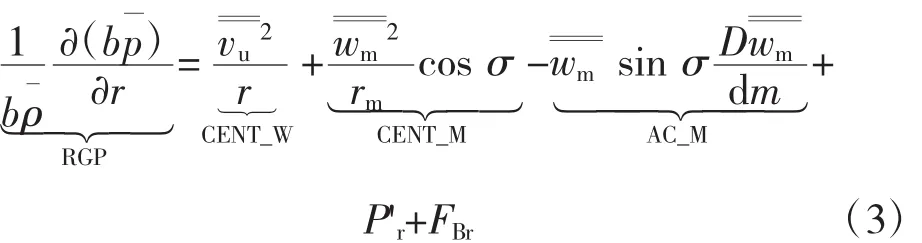
式中：等式左边为径向压力梯度（RGP）；等式右边分别为周向速度引发的离心加速度项（CENT_W）、由于子午流线的曲率而引发的离心加速度的径向分量（CENT_M）、子午速度变化所引发的加速度的径向分量（AC_M）、周向脉动源项的径向分量 P'r，P'r与 Pr的区别在于二者的比值为密度，而下面将仍以Pr表示周向脉动源项的径向分量，并不再重复说明；FBr为无黏叶片力的径向分量，由于主要分析周向不均匀性对叶片通道进口流动平衡的影响，该处FBr=0，因此后面将不给出FBr的分布情况。

1.2 周向不均匀性的应力输运模型

类似雷诺平均后所产生的雷诺应力项，式（1）中的周向脉动应力项代表着周向不均匀性所带来的影响，本节将简要介绍周向脉动应力项的应力输运模型，详细建模过程可参考文献[20]。类比湍流模型中的应力输运模型，可以推导出对于周向脉动应力项的应力输运方程，以张量形式表示的无黏形式的应力输运方程为

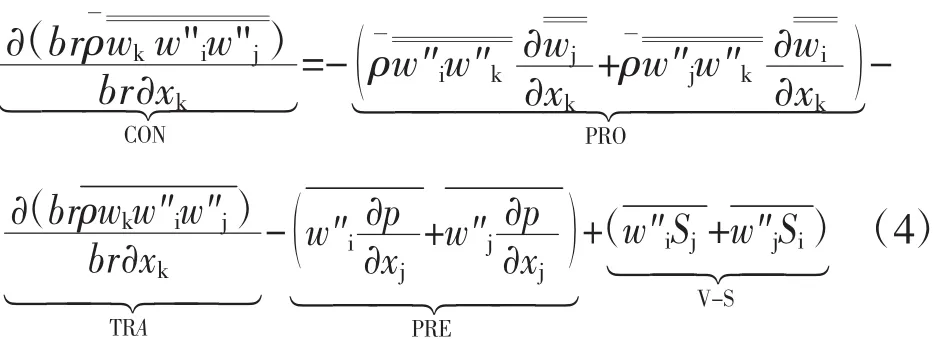
式中：方程左侧为对流项（CON）；右侧分别为生成项（PRO）、输运项（TRA）、速度 -压力关联项（PRE，简称压力项）以及速度-源项（V-S）关联项，其中生成项表征应力输运方程与平均后的轴对称流场之间的关联，速度-压力关联项表征由于压力的脉动性而做的功，输运项、压力项及速度-源项关联项均无法直接获得，需要进行建模，而在这几项中，压力项为关键项，其余几项则可忽略，因此下面简要介绍压力项的建模方法，详细过程可参考文献[20]。

假设速度和压力可沿周向进行傅里叶级数展开，并保留到1阶，则压力项可进一步推导为

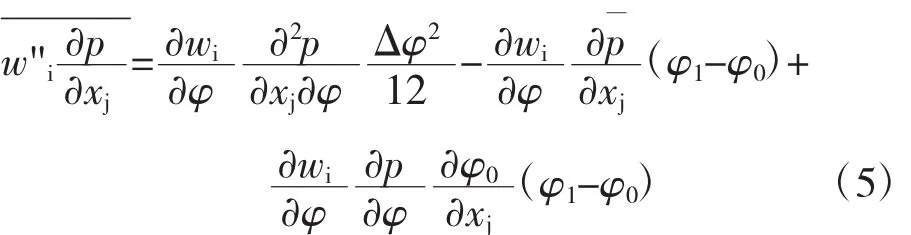
考虑到密度加权平均的定义，φ0和φ1之间满足关系

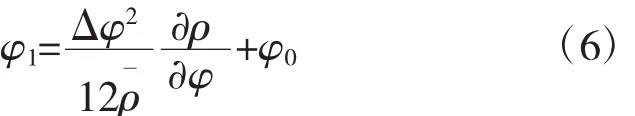
从式中可见，当确定3个速度和压力的周向偏导数后，可解出压力项。进一步引入S2流面无黏形式的周向动量方程以及绝对坐标系下流动无旋假设，并结合连续方程和无黏形式下的能量方程，可推导出压力和3个速度分量的周向偏导数，其形式为

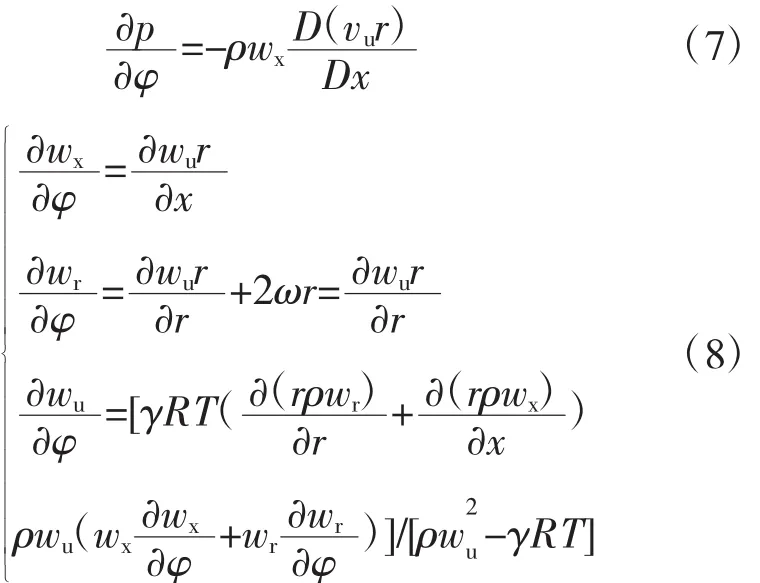
由此可实现对压力项的求解，从而实现应力输运方程的封闭。另外从式（7）、（8）中可见，引发速度和压力的周向不均匀性的1个主要因素是环量沿轴向和径向的偏导数，即负荷的分配情况，而文献[21]中也基于S2流面上周向动量方程分析了周向不均匀性产生的原因，认为对于定常问题周向不均匀性来源于黏性力的存在和气流的环量沿流线的导数不为零，而在未发生大范围分离时，相比黏性力，环量改变所反映的无黏叶片力是最主要的源项，因此环量改变对周向不均匀性的产生应起主要作用。

环量的分布特征在设计问题中是给定量，在分析问题中则主要是源于无黏叶片力的作用，因此该模型同时适用于设计问题和分析问题。

2 应力输运模型的验证及周向不均匀性的影响分析

2.1 研究对象及计算方法

采用1个前掠20°叶栅作为研究对象，该叶栅基元的厚度分布采用文献 [22]中的设计进口马赫数为0.62的可控扩散叶型，中弧线采用任意造型的方式获得。叶栅的基本参数见表1。由于缺乏试验数据作为验证，本文采用3D数值模拟的结果作为基准，并应用了NUMECA FINE/Turbo3D数值模拟软件对各叶栅算例进行数值模拟研究。通过对某单级跨声速风扇、某风扇/增压级以及某单级离心压气机的数值计算结果与试验结果的对比校核，NUMECA FINE/Turbo的计算精度能够满足压气机设计过程中的流场验算和分析[23]。边界条件的设置为：在计算域的进口处给定总温、总压以及气流方向，通过改变进口气流角来获得不同的名义迎角，这里的名义迎角是指远前方均匀来流气流角与叶片几何进口角的夹角，后面简称为迎角，给定的名义迎角为0°、±2°和±4°；采用当地迎角的概念，即叶片通道进口处气流角与叶片几何进口角的夹角。在出口给定流量以控制进口马赫数，对于各个迎角，进口马赫数均为0.62；环壁和叶片表面采用绝热无滑移边界。湍流模型采用Spalart-Allmaras（S-A）方程模型，网格划分保证固壁面第1层网格单元y≤10。3D数值模拟计算网格采用AUTOGRID模块自动生成，如图1所示。对于不同迎角算例，均采用同一套网格，总网格数约为162万。

表1 叶栅基本参数

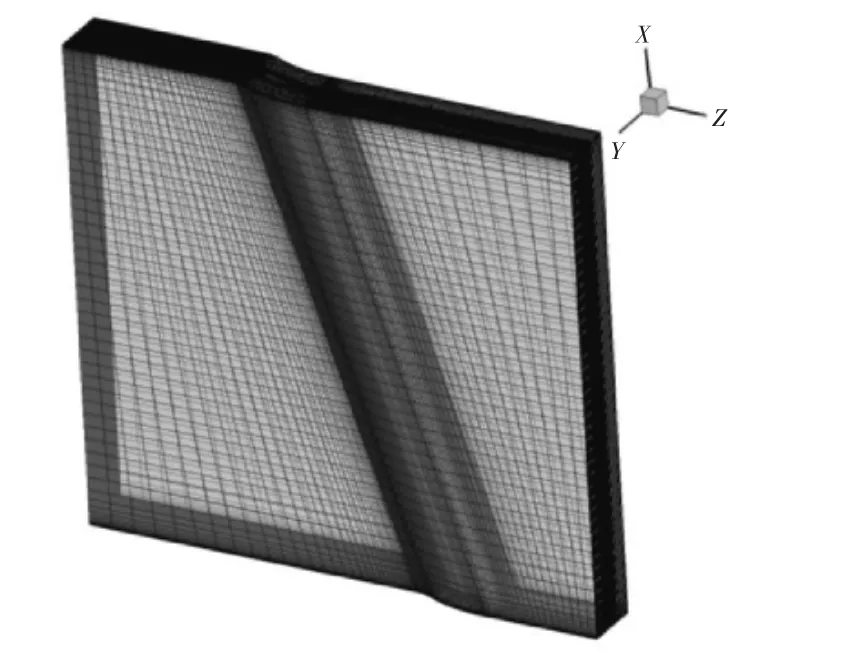
图1 3D数值模拟网格

另外，为分析周向不均匀性的影响，开展了以下2种类型的周向平均通流计算：

（1）CAM：未考虑周向不均匀性的周向平均通流计算；

（2）CAM+MODEL：加入了以应力输运模型计算的周向脉动应力项的周向平均通流计算。

周向平均通流模型的计算网格如图2所示，总网格数为3185。通流模型采用基于时间推进的有限体积方法来求解控制方程，时间离散格式为显式格式为Jameson4步Runge-Kutta法。对无黏通量的空间离散采用Edwards[24]提出的低耗散通量分裂格式（LDFSS）。对于边界条件的设置，进出口边界条件与3D数值模拟相同，环壁采用对称边界条件。

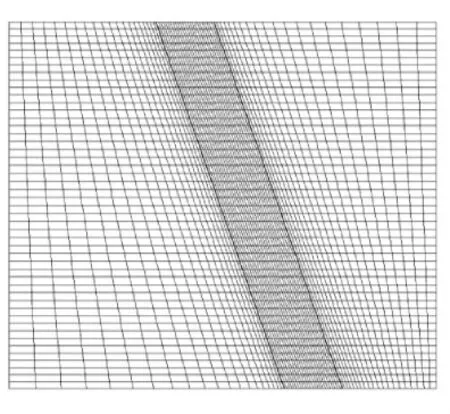
图2 通流计算网格

本文主要关注的是周向不均匀性对叶片通道进口流场的影响，此处黏性作用不明显，虽然无黏叶片力在此处为0，但压力势已经会以周向不均匀性的形式造成一定影响，下面将分别从叶片通道进口气流角和径向平衡的角度进行分析。

2.2 周向不均匀性对叶片通道进口流动参数的影响

为考察迎角改变时周向不均匀性对叶片通道进口流场的影响，首先分析在引入周向不均匀性后叶片通道进口气流角的变化，本节将靠近叶片前缘处的气流角与计算域进口气流角做差以便于分析这一变化，结果如图3所示。从图3（a）中可见，对于20%展高处，随着迎角的增大，3D和CAM预测的差值有一定的增长趋势，而CAM+MODEL则呈现出下降趋势，这主要是由于随着迎角增大，Pu的作用增强（图4（a）），导致周向速度变化更大，但总体来说CAM+MODEL所预测的差值CAM要更接近3D的，在名义迎角从-4°增大到4°的过程中，CAM+MODEL与CAM所预测的气流角差值间的偏差量从约0.1°增加到了约0.7°，预测精度提高了25%以上；对于50%和80%展高处，在加入周向不均匀性的影响后，对气流角的预测精度同样提高，并且随着名义迎角的增大，3D和CAM+MODEL预测出的αLE-αinlet的值均呈现出下降趋势；与20%展高处的结果类似，加入周向不均匀性模型后通流模型对气流角改变量的预测精度也同样有所提高，提高50%以上。

图3 掠叶栅不同展高处αLE-αinlet随名义迎角的变化

由于叶片通道进口处无黏叶片力为0，因此上述气流角的改变是由于周向不均匀性所诱发的，周向脉动源项的轴向和周向分量Px、Pu会分别影响叶片通道进口轴向和周向速度，从而造成气流角的改变，并且随着迎角的增大和负荷的提高，周向不均匀性的影响也在增大。

由于Pu会对环量造成影响，因此对其预测是否准确很重要。叶栅不同展高截面叶片上游距前缘约4%弦长处无量纲Pu随迎角的变化情况如图4所示，其中Pu是由计算域进口对应流动参数进行的无量纲化。对于3个不同展高处，Pu的分布呈现出相近的特征，都是随着迎角的增大Pu的绝对值增加，说明其作用将增强。此外，对于不同迎角，应力输运模型计算得到的Pu与3D结果的偏差在不同截面都很小，都在20%以内，说明对于非设计工况，应力输运模型能够很好地预测周向脉动源项。

在加入应力输运模型后，通流模型的计算时间比未加入应力输运模型时的约增加40%，这是由于在主控方程中加入6个微分方程，但计算时间仍远远少于3D数值模拟。各算法的计算时间见表2。

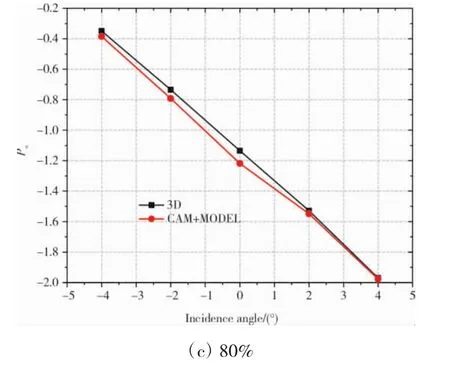
图4 周向分量Pu随名义迎角的变化掠叶栅不同展高处周向脉动源项

2.3 周向不均匀性对叶片通道进口流动径向平衡的影响

上述分析表明，在加入周向不均匀性后，叶片通道进口气流角发生了改变，即当地迎角发生了改变。对于掠叶栅，各展向截面当地迎角的变化会改变叶片负荷沿展向的分布情况，进而改变进口径向流动平衡。为进一步考察名义迎角和当地迎角改变对径向平衡的影响，给出了不同名义迎角下叶栅上游距前缘约4%弦长处径向平衡方程（3）中各项沿展向的分布情况（如图5所示），并以流道进口的流动参数对这些项进行了无量纲化。图中的命名规则以“-2_3D”为例，其中-2表示名义迎角为-2°，3D指3维计算的结果。

对比图 5（a）～（e）中各项，从量上来看，与 RGP处于同一量级的项为CENT_M和Pr，而CENT_W和AC_M则要比其余3项小1～2个量级，表明周向不均匀性明显影响叶片通道进口径向平衡及径向压力梯度。

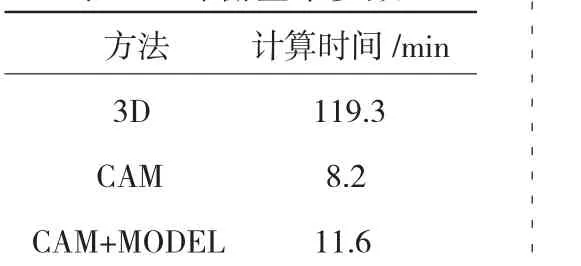
表2 叶栅基本参数

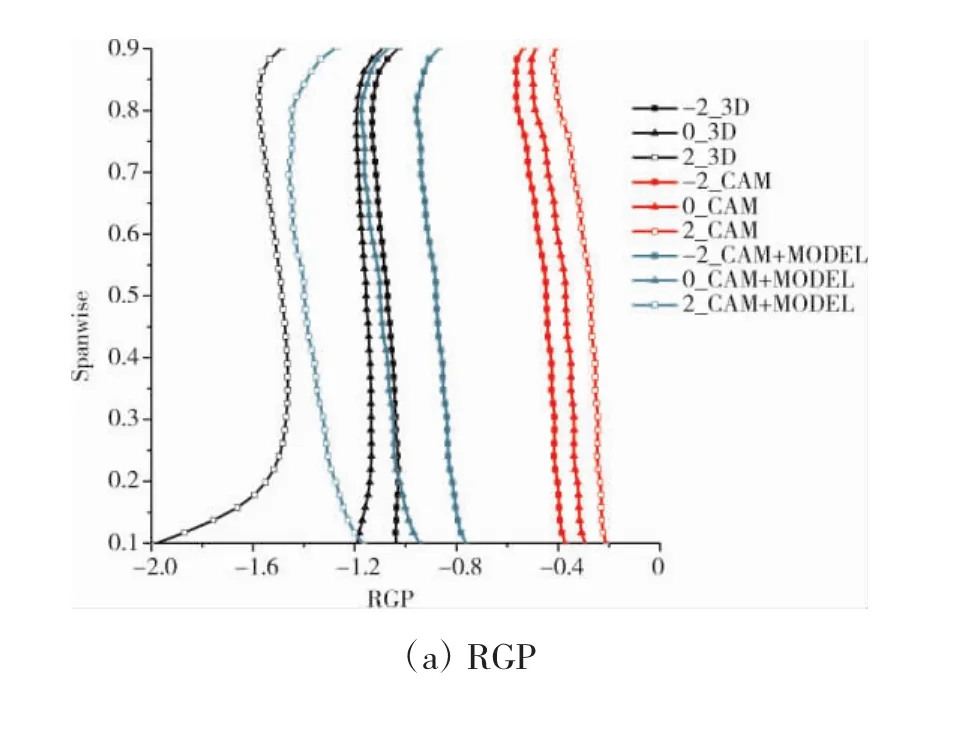
图5 掠叶栅进口径向平衡参数沿展向的分布随名义迎角的变化

对于RGP随名义迎角的变化情况（图5（a）），对于 3D 结果，迎角从 -2°～0°增大时，RGP 有所减小，但并不明显；而从0°～2°增大时，RGP的值则明显减小。这说明名义迎角的增大会使径向压力梯度得到加强，而CAM的结果中RGP随着名义迎角的增大则呈现出相反的趋势，对径向压力梯度变化的描述不足。在加入周向不均匀性的影响之后，CAM+MODEL计算得到的各名义迎角下RGP的分布都更接近3D结果，随迎角的变化趋势也要更接近3D结果。结合图5（b）～（e）可见，在加入周向不均匀性的影响后，RGP的变化主要来源于CENT_M和Pr，并且Pr对于RGP的变化起主要作用。

对于CENT_W（图5（b）），3D、CAM+MODEL和CAM之间的偏差反映出周向分速度的变化，即在靠近叶片通道进口处环量已经由于周向不均匀性的作用而发生改变。CAM+MODEL相比CAM偏离3D更多，说明加入周向不均匀性模型后通流计算得到的vu所受到的影响要大于3D数值模拟，但从图中横坐标的数值可见，CAM+MODEL与CAM和3D之间的实际区别并不大。而从趋势上来看，CAM与3D之间确实存在偏差，而且在加入周向不均匀性模型后，CAM+MODEL的结果向着3D的方向移动，表现出了一定的一致性，说明在叶片通道进口vu确实会由于周向不均匀性的作用而发生改变；此外，当迎角从-2°～2°增大时，CAM与3D之间的偏差增大，反映出了周向不均匀性的作用在增强，与此同时，CAM与CAM+MODEL之间的偏差也随着迎角的变化呈现出了相似变化，说明加入周向不均匀性模型后通流模型能够与3D数值模拟一样反映出负荷变化对叶片通道进口流场的影响。

CENT_M（图 5（c））在名义迎角从 -2°～2°增大后，其值呈现出减小趋势，说明迎角增大后子午流线曲率增大。而CAM对CENT_M的预测要高于3D的结果，趋势也相反；在引入周向不均匀性的影响后，CAM+MODEL所预测的CENT_M的精度有所提高，可达60%以上，趋势也与3D一致，说明加入周向不均匀性影响后通流模型能够更好地刻画子午流线曲率。

AC_M（图5（d））在名义迎角发生改变时变化并不是很明显，其值略有增加。在引入周向不均匀性的影响后，CAM+MODEL的分布相比CAM更接近3D。

从图5（e）中可见，随着名义迎角的增大，周向脉动源项的径向分量Pr的绝对值增大，反映出负荷沿展向有增大的趋势。此外，应力输运模型计算得到的Pr的分布与3D结果基本一致，最大偏差在50%以内。

综上所述，CAM+MODEL能够得到与3D相接近的分布，说明应力输运模型在迎角改变的情况下有能力反映出与3D计算相近的周向不均匀性的影响，提高通流计算的预测精度。同时，加入周向不均匀性后，通流模型能够更好地反映出掠叶栅在不同迎角下流场中周向不均匀性的影响。

3 结论

研究表明，周向不均匀性会对叶轮机流场造成影响，因此有必要在通流模型中计入周向不均匀性的影响，以使其更好地计入真实3D流动效应，提高设计、分析通流模型的预测精度。为模化并分析迎角改变时掠叶栅进口流动周向不均匀性的影响，本文将1种模化周向平均通流模型中周向脉动应力项的应力输运模型结合到周向平均通流模型中，针对掠叶栅在不同迎角下的结果对比分析了该模型的可行性及周向不均匀性的作用，得出了以下结论：

（1）随着迎角的增大，周向脉动源项的绝对值及其对叶片通道进口流场的影响都随之提高，在本文算例中受周向不均匀性的影响叶片通道进口气流角的改变量可达0.7°。

（2）在加入周向不均匀性模型后，在迎角改变的条件下通流计算预测的进口气流角均更接近3D结果，对叶片通道进口气流角的改变量的预测精度普遍提升30%以上，对叶片通道进口流动径向平衡的描述精度提高60%以上。引入周向不均匀性有助于提升通流分析软件对采用掠设计的压气机流场的计算精度。

（3）对于处于不同迎角下的叶栅流场，该应力输运模型都能较好的预测出周向脉动源项，在前缘前模型预测结果与3D结果的相对偏差普遍在20%之内，最大不超过50%。

（4）由于应力输运模型在主控方程中增加了6个微分方程，因此对通流模型的计算时间影响较大，加入该模型后计算时间在原通流模型的基础上增加了约40%，但仍远远少于3D数值模拟所用时间。该模型将周向不均匀性与环量分布关联，可以为设计或分析问题提供周向脉动应力项的预测。