杆件缺失位置对点阵夹芯结构固有频率的影响规律

张 凯，陈建恩

（天津理工大学天津市先进机电系统设计与智能控制重点实验室机电工程国家级实验教学示范中心，天津300384）

夹芯结构是由上下面板和中间的芯层所构成的，由于其高比刚度、高比强度、优异的隔热性能和巨大的能量吸收潜力，在运输、航空和汽车领域得到了越来越多的应用.以往常用的芯层材料有蜂窝材料和泡沫材料，而在2000年，由国外一些学者提出了一种新型的空间点阵材料.它是模拟分子点阵构型制造出的周期性超轻多孔材料.其典型构型包括金字塔型、四面体型、Kagome等.相比于蜂窝和泡沫夹芯结构，点阵夹芯结构的性能更为优异，应用前景更加令人瞩目.因此，对于夹芯结构的相关力学特性进行研究是很有必要的.

目前，国内外学者在压缩、弯曲性能、冲击、弹道响应以及振动特性等方面对点阵夹芯结构进行了相关研究.Li等人[1]从振动特性考虑，提出了一种检测点阵夹芯结构杆件脱落的方法，用于夹芯结构的损伤定位.冀宾等人[2]对点阵夹芯板在受到面内压缩载荷时的力学行为进行了研究，显示出点阵材料的应用潜力.张弥等人[3]分别通过理论、试验、数值模拟这三种方法来研究两端简支的3D打印钛合金金字塔型点阵夹芯结构在三点弯曲载荷下的响应.龙连春等人[4]为了研究夹芯梁单胞变化对结构承载能力的影响，建立了点阵夹芯结构的优化设计模型，目标函数为结构刚度最大，约束条件为体积和单胞尺寸，对夹芯梁单胞的尺寸分布进行了优化设计，并以四面体单胞夹芯结构的优化设计为例进行详细说明.Deshpande和Fleck[5]研究了四面体点阵夹芯梁在三点弯曲作用下的破坏响应.翟彦春等人[6]分析了粘弹性层厚度对复合材料夹芯梁自由振动的影响.毛毅凝等人[7]研究了3D-Kagome点阵夹芯板在高斯白噪声激励下横向非线性振动的响应统计特性.钱若立等人[8]采用逐层/实体元的方法，研究金字塔型点阵夹芯梁结构在不同边界条件下的静力与自由振动问题.雷鹏福等人[9]在现有点阵结构整体建模技术的基础上，提出一种点阵结构节点强化技术，能在点阵结构节点处实现自然圆角过渡，从而改善其力学性能.仲梁维等人[10]针对点阵材料结构设计困难的问题，建立了由长方体空间衍生的胞元结构的数学模型、试件的参数化模型及力学性能研究系统.张征等人[11]采用有限元软件Abaqus建立了金字塔点阵结构单胞的平压和剪切模型，并且发现复合材料不同的铺层角度和铺层数会对材料的刚度、比刚度、模量和比模量产生一定影响.闫国良等人[12]研究了影响点阵夹芯结构换热性能的因素，采用翅片法推导四面体型点阵结构等热流密度和等壁面温度边界条件下的努塞尔数，以此表征结构的换热性能，并与实验结果进行对比.王祖华和殷洪[13]研究了芯层含多种祖分的含空腔点阵增强夹芯结构的固有振动特性.韩笑等人[14]对多层梯度点阵夹芯板在爆炸载荷下的动态响应进行了模拟研究.郑权等人[15]基于增材制造工艺制备多层金字塔型点阵夹芯板，并根据标准测试方法进行准静态平压破坏实验，得到多层金字塔点阵结构的抗压缩强度.陈锋等人[16]通过实验手段和有限元方法针对含孔碳纤维增强树脂基复合材料点阵夹层结构在面外载荷作用下的失效模式及其影响因素进行了研究.励争等人[17]采用有限元数值计算和实验的方法研究了轻质点阵夹芯板在热载荷作用下的稳定性问题.周楠等人[18]描述了泡沫铝及夹芯复合材料的制备方法和应用，研究了泡沫铝夹芯复合材料的抗爆抗侵彻性能.

在对点阵结构缺陷方面的研究，目前较多的集中于蒙皮受到外部冲击破坏之后，点阵结构整体的破坏情况，而很少涉及到内部芯层单独受损的问题.本文以金字塔型点阵夹芯梁为例，在悬臂的边界条件下，使芯层分别缺失一个、两个、四个单胞所含杆件，改变缺失杆件的位置，分析不同位置的杆件缺失对于夹芯梁固有频率的影响规律.并且在此基础上，改变杆件半径，研究芯层缺陷位置及半径同时变化对固有频率的影响.

1 有限元仿真设置及验证

为确保分析结果的正确性，本文分别采用Ansys workbench和Abaqus两种软件对点阵夹芯梁进行仿真，通过比较所得梁的固有频率来验证有限元仿真设置的正确性.

1.1 点阵夹芯梁结构描述

本文研究的对象为金字塔型点阵夹芯梁，运用Solidworks软件进行实体建模，模型如图1所示.夹芯梁长度方向取20个单胞，宽度方向取4个单胞.夹芯梁结构参数为：蒙皮厚度为1 mm，芯层杆件半径为1 mm，杆件倾斜角为45°，芯层高度为15 mm，单胞底面边长为21 mm.夹芯梁蒙皮和芯层材料均为铝合金，材料参数为：材料密度ρ=2 770 kg/m3，弹性模量E=71 GPa，泊松比ν=0.33.

图1金字塔型点阵夹芯梁模型图Fig.1 Model of pyramidal truss core sandwich beam

1.2 Ansys workbench仿真

选取三个模型进行分析，第一个模型去除了中间两行第一和第二列的四个单胞，根据单胞缺陷的位置，将其编号为1.第二个模型去除了第九和第十列的四个单胞，编号为2.第三个模型去除了第十九列和第二十列的四个单胞，编号为3，分别如图2（a）-（c）所示.将模型导入Ansys workbench中进行有限元仿真，采用四面体网格，选择patch conforming算法，夹芯梁的左端面固定，右端面自由，使其处于悬臂状态.

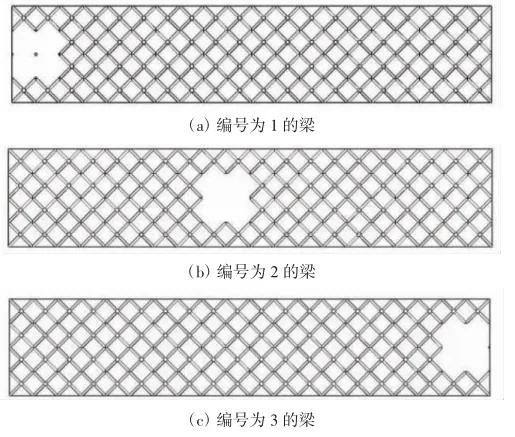
图2含芯层缺陷的点阵夹芯梁模型图Fig.2 Models of truss core sandwich beams with coredefects

1.3 Abaqus仿真

将上述的三个模型导入Abaqus中进行有限元仿真，仿真所需的材料参数及边界条件与Ansys workbench设置相同，网格在选定为四面体单元之后，选择默认算法，根据默认的设置，在边界面上的部分区域使用映射的三角形网格.

1.4 固有频率比较

通过有限元仿真，得到了夹芯梁在不同缺陷状态下的前三阶固有频率.两种软件仿真所得的固有频率如表1所示，另外，给出了夹芯梁在缺陷位置为1时的前三阶振型，结果由Ansys workbench仿真所得，如图3（a）-（c）所示.

表1不同缺陷位置下Ansys workbench和Abaqus所得的前三阶固有频率Tab.1 The first three natural frequencies of Ansys workbench and Abaqus at different defect positions Hz

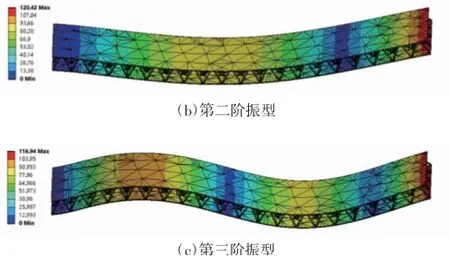
图3缺失位置为1的夹芯梁的前三阶振型Fig.3 The first three mode shapes of beam with missing position

2 芯层缺陷位置变化

为了研究不同位置的杆件缺失对于点阵夹芯梁固有频率的影响，在完整夹芯梁的基础上，删除不同位置单胞所含的杆件，然后利用有限元仿真得到夹芯梁的固有频率.两种软件所得的仿真结果一致，节省篇幅起见，本文仅给出了Ansys workbench的计算结果.

2.1 中间一行各列单胞所含杆件缺失的情况

选取了夹芯梁中间一行，依次去掉各列单胞所含杆件，计算固有频率.其中，完整梁的缺失位置记为0，其他梁根据缺失位置记为1-20，缺失位置为1的梁如图4（a）所示.得到前三阶固有频率随着缺失位置的变化情况，如图4（b）-（d）所示.

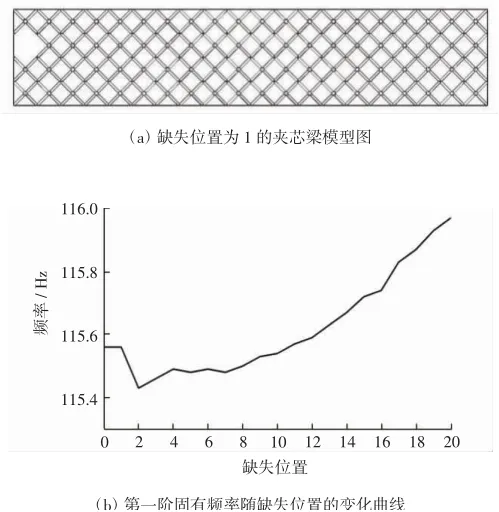
图4中间一行各列单胞缺失的夹芯梁模型图及前三阶固有频率随缺失位置的变化曲线Fig.4 Model diagram of the sandwich beam with missing cells in the middle row and the variations of the first three natural frequencies along with missing position

含单个单胞杆件缺失的夹芯梁第一阶固有频率与完整梁的第一阶固有频率相比，最大差值为0.41 Hz，第二阶固有频率的差值为4.56 Hz，第三阶固有频率的差值为16 Hz.另外，含缺陷的夹芯梁之间，第一阶固有频率之间最大差值为0.54 Hz，第二阶固有频率的差值为6.1 Hz，第三阶固有频率的差值为22.4 Hz.由上图可以看出，缺失位置为1时，第一阶固有频率并没有发生变化，而第二阶和第三阶固有频率均下降.随着缺失位置与固支端距离的增加，第一阶固有频率起初有小幅减小，之后则呈上升趋势，然而第二阶固有频率变化稍显复杂，呈现出波动的状态，第三阶固有频率波动的现象更甚，频率的变化规律更加复杂.

2.2 中间两行各列单胞所含杆件缺失的情况

选取夹芯梁中间的两行，依次去掉各列单胞所含杆件，计算夹芯梁的固有频率.缺陷位置编号与之前设置一致.缺失位置为1的梁如图5（a）所示.得到的固有频率结果如图5（b）-（d）所示.

图5中间两行各列单胞缺失的夹芯梁模型图及前三阶固有频率随缺失位置变化曲线Fig.5 Model diagram of the sandwich beam with missing cells in each column of the middle two rows and the variations of the first three natural frequencies along with missing position

中间两行各列单胞缺失的夹芯梁的第一阶固有频率与完整梁固有频率最大差值为0.87 Hz，第二阶固有频率的差值为11.64 Hz，第三阶固有频率的差值为43 Hz.含芯层缺陷的夹芯梁之间，第一阶固有频率最大差值为1.2 Hz，第二阶固有频率的差值为14.83 Hz，第三阶固有频率的差值为51.9 Hz.

由图5可以看出，两个单胞缺失的频率变化情况总体来说与单个单胞缺失的情况一致.所不同的是，第一阶固有频率在缺失第一列单胞时就有所降低.另外，第二阶固有频率在缺失位置8-12区间内变化比较平缓，第三阶固有频率则是在9-11和13-15区间内变化较为平缓.

2.3 中间两行相邻两列单胞所含杆件缺失的情况

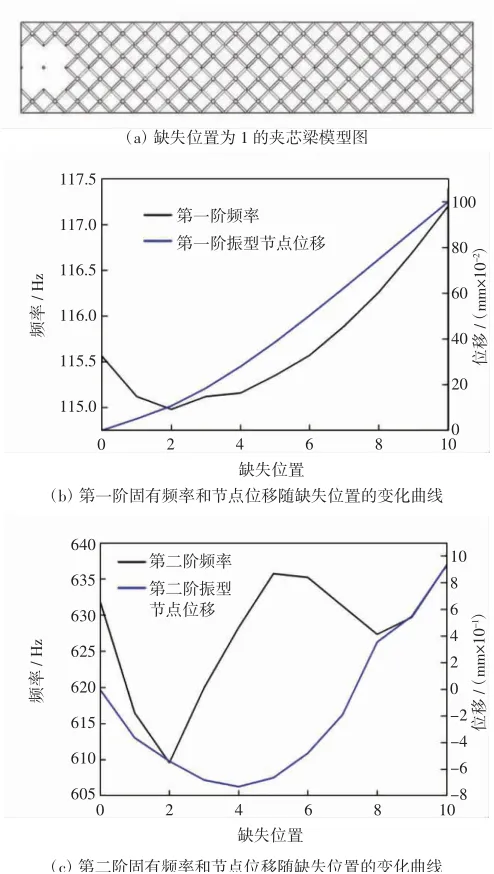
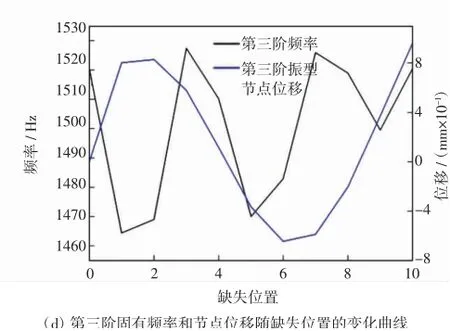
图6中间两行相邻两列单胞缺失的夹芯梁模型图以及前三阶频率和节点位移随缺失位置的变化曲线Fig.6 Model diagram of the sandwich beam with two adjacent columns of cells missing in the middle two rows and the variations of the first three frequencies and node displacements along with missing position

选取了夹芯梁中间两行，依次去掉相邻两列单胞所含杆件，然后计算固有频率.这种情况下，缺失位置分别标记为1-10，其中缺失位置为1的梁如图6（a）所示，得到的固有频率结果如图6（b）-（d）所示.此外，图6中给出了夹芯梁上各节点的最大位移，即模态振型.提取模态振型的方法为：选择沿长度方向的各单胞所对应的上面板中心节点，以上面板所在平面为零位移平面，读取各节点沿z轴方向的最大位移并进行作图.

中间两行相邻两列单胞缺失的夹芯梁的第一阶固有频率与完整梁第一阶固有频率的最大差值为1.64 Hz，第二阶固有频率的差值为22.35 Hz，第三阶固有频率的差值为56.1 Hz.含芯层缺陷的夹芯梁之间，第一阶固有频率最大差值为2.22 Hz，第二阶固有频率的差值为27.28 Hz，第三阶固有频率的差值为63 Hz.由上图可知，第一阶固有频率变化规律比之前两种缺陷情况都更为平滑，但是第二阶和第三阶固有频率并没有出现第二种缺陷情况所含的平滑区间.通过比对固有频率和模态振型随缺失位置的变化曲线，可以看出，第二和第三阶固有频率随缺失位置的变化曲线的峰值，总是位于对应振型的波腹的两侧.

3 芯层缺陷位置和杆件半径同时变化

针对上述所得结果，分别对三种情况作了进一步讨论，研究了点阵夹芯梁在芯层缺陷位置和杆件半径同时发生变化时，其固有频率的变化情况.

芯层杆件半径分别取0.6 mm、0.8 mm、1.0 mm、1.2 mm、1.4 mm，三种芯层缺陷状态下得到的固有频率变化情况分别如图7-9所示.

图7第一种情况下前三阶固有频率随缺失位置和杆件半径变化的三维图Fig.7 The first three natural frequencies change with the missing position and the member radius in the first case

图8第二种情况下前三阶固有频率随缺失位置和杆件半径变化的三维图Fig.8 The first three natural frequencies change with the missing position and the member radius in the second case

图9第三种情况下前三阶固有频率随缺失位置和杆件半径变化的三维图Fig.9 The first three natural frequencies change with the missing position and the member radius in the third case

由图可知，当杆件半径取不同值时，其固有频率随缺失位置的变化趋势与杆件半径为1 mm时呈现的规律相似.在不同的杆件半径条件下，随着缺陷由固支端向自由端变化，第一阶固有频率均表现出先减小后增大的趋势，而第二阶、第三阶固有频率均表现出降低升高交替出现的现象，并且对于第三阶固有频率这种特征要更明显.

在缺失位置不变时，第一阶固有频率随着杆件半径的增大，整体呈下降趋势，而第二阶固有频率整体上随着半径的减小而减小，但半径为1.2 mm的频率要高于1.4 mm时的频率，且半径为0.6 mm时的频率要明显低于其他半径条件下的固有频率，第三阶固有频率随半径减小而减小，无特殊情况.

接着，利用Origin软件的nonlinear surface选项进行曲面拟合，分别得到三种情况下的前三阶固有频率关于杆件半径和缺失位置的函数，对于第一种情况，第一阶固有频率的表达式为

其中，Z表示固有频率；X表示缺失位置；Y表示杆件半径.

4 结论

本文研究了金字塔型点阵夹芯梁在含芯层缺陷时的固有频率.分别研究了芯层在缺失一个、两个、四个单胞所含的杆件时夹芯梁的固有频率变化，研究发现，三种情况下其前三阶固有频率随缺陷位置的变化情况较为相似.随着杆件缺失位置与固支端距离的增加，第一阶固有频率先减后增，并且最终频率要高于无损梁.但是随着频率阶次的增加，固有频率的变化趋势逐渐复杂，呈现出一种波动的状态.另外，值得注意的是，固有频率的变化曲线与夹芯梁的振型图在形态上存在联系，第三种情况下第二和第三阶固有频率变化曲线的峰值存在于对应振型的波腹两侧.

然后研究夹芯梁在不同的缺陷状态和杆件半径条件下，其固有频率的变化情况.结果显示，杆件半径不同时，夹芯梁的固有频率随缺失位置的变化规律与杆件半径1mm时呈现的规律基本一致.而在缺失位置一定时，第一阶固有频率随杆件半径的增大而减小，第二阶和第三阶固有频率则增大，但在某些特定半径值时，第一阶和第二阶固有频率又会出现反常现象.为此，对不同缺陷、不同杆件半径条件下的前三阶固有频率进行函数拟合，用拟合函数来定量描述三者之间的关系，利用该函数可以较为准确地计算所选的缺陷位置和杆件半径范围内的固有频率.