基于未知声速的水下三维单信标定位模型
朱仲本,田瑞菊,许培龙
(哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
0 引 言
海洋因其重要的战略地位和丰富的矿物资源成为研究的热点,水下无人航行器越来越受到重视。水下无人航行器可搭载多种传感器、专用设备或武器模块,在军事领域广泛应用于水下监视侦察,收集情报,探雷、猎雷和灭雷,跟踪打击等诸多领域,在将来海洋战争中具有重要地位。另外,无人航行器还可用于海底打捞、海底资源勘探和开发等,具有非常重要的民用价值。水下无人航行器的精准定位对于确保这些应用所收集数据的准确性至关重要,水下定位技术可以保证航行器获得实时位置信息,是水下航行器进行水下科研或生产活动的关键技术,是其顺利完成既定工程任务的保障。
水下定位技术主要包括惯性导航定位技术[1-2]和声学导航技术。声学导航技术包括长基线(Long Base Line,LBL)定位系统[3]、短基线(Short Base Line,SBL)定位系统[4]、超短基线(Ultra Short Base Line,USBL)定位系统[5]及水下单信标定位系统[6]等。现有的水下定位技术能够满足各种定位要求,但也存在缺点。例如:将LBL定位系统应答器设置海底是一个耗时过程;USBL定位系统典型的定位精度为深度的1%~2%;惯性导航定位系统成本较高,并且在每次部署之前需进行对准工作。相比于其他定位技术,水下单信标定位具有安装使用简单、成本低、便于远距离拓展等优点,在水下航行器定位上具有广阔的应用前景。水下单信标定位技术主要通过测量传播时间获得已知位置的水声信标与航行器或待定位目标之间的地理斜距,利用距离信息和航行器本身的惯性传感器信息经过一定滤波算法获得航行器水下位置信息。
传统的水下单信标定位模型通常考虑航行器在二维运动状态下建立动力学模型,但实际过程中航行器在三维状态下运动,因此考虑在三维状态下基于卡尔曼滤波的水下单信标定位五状态变量模型(State Variables Model,SVM)[7](简称“5-SVM”),通过引入水深构建一种新型水下单信标定位模型,主要包括其运动学模型、量测模型及过程噪声模型。同时通过仿真数据,利用卡尔曼滤波输出对比新型水下单信标定位模型与5-SVM,评估2种模型的位置估计精度。
1 定位模型构建
1.1 水下单信标定位5-SVM
考虑海洋航行器二维运动情况,建立笛卡尔坐标系,如图1所示。以水声信标所在位置为坐标原点,建立水平面内坐标系xOy,航行器位于(x,y)点时,其相对于水的运动速度为vw,航向角为ψ,海流速度为vc,有效声速(Effective Sound Velocity,ESV)为ve。

图1 二维笛卡尔坐标系
以水的运动速度vw、航向角ψ为控制变量,航行器位置坐标(x,y)、海流速度vc及ESVve为状态变量,建立基于卡尔曼滤波的传统水下单信标定位模型,其运动方程为
(1)
式(1)可进一步简写为
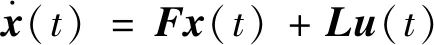
(2)
式中:


式(2)为静态线性时不变方程,其通解[8]为
x(t)=exp[F(t-t0)]x(t0)+
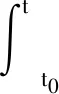
(3)
将式(3)进行离散处理,令Δt=t-t0,得:
xk=Ak-1xk-1+Bk-1uk-1+wk-1
(4)
式中:xk为系统状态变量;Ak-1为状态转移矩阵;Bk-1为系统控制项系数矩阵;uk-1为系统控制项矩阵;wk-1为系统的随机动态噪声。其中:

式(4)中在tk时刻的离散状态变量xk记为
(5)
系统相应的过程噪声项wk记为
wk=[wx,k-1wy,k-1wcx,k-1wcy,k-1we,k-1]T
(6)
采用水声信号传播时间为系统量测变量,即
mk=Tk,t+vt,k
(7)
式中:mk为水声信号传播时间的量测值;Tk,t为水声传播时间;vt,k为该水声信号传播时间的测量噪声。
式(7)可表达为系统状态变量x中xk、yk、zk的函数,记为hk,其表达式为
(8)
式中:(xb,yb,zb)为单信标的位置坐标;ve,k为k时刻的有效声速。此处航行器的深度zk由深度传感器测量得到,视为已知量。

(9)

5-SVM水下单信标定位模型噪声项如式(6)所示,将5个噪声变量分为3组:(1)wx,k-1和wy,k-1为在x和y方向的位置变化率噪声;(2)wcx,k-1和wcy,k-1为在x和y方向的海流变化率噪声;(3)we,k-1为ESV变化率噪声。假设这3组噪声变量相互独立,则噪声向量wk对应的离散方差矩阵Qk为
(10)
式中:Qp,k为wx,k和wy,k的协方差矩阵(wx,k和wy,k相关);Qc,k为wcx,k和wcy,k的协方差矩阵(假设wcx,k和wcy,k不相关);Qe,k为we,k的方差。
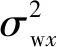
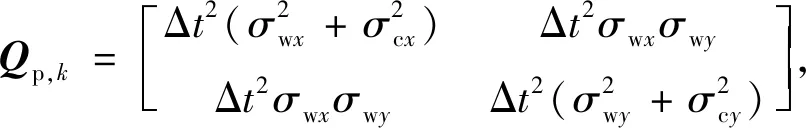
将系统状态变量x中x和y进行离散,得:
(11)
进而可得wx,k和wy,k的协方差矩阵Qk,将Qp,k、Qc,k和Qe,k代入式(10),得:
(12)
海流速度量测值表示为
(13)
式中:vcx,k和vcy,k分别为k时刻海流速度在x轴和y轴的分量;υcx,k和υcy,k分别为海流量测噪声在x轴和y轴的分量。
海流速度相应量测矩阵为
(14)
1.2 新型水下单信标定位模型
将深度作为新的状态变量,在5-SVM基础上进行拓展得出6-SVM。
考虑海洋航行器三维运动情况,建立三维坐标系Oxyz,以水的运动速度vw、航向角ψ为控制变量,航行器位置坐标(x,y,z)、水流速度vcx、vcy及ESVve为状态变量,建立基于卡尔曼滤波的水下单信标定位6-SVM,其运动方程为
(15)
式中:z为航行器深度。
将方程的解进行离散,得到与式(4)相同的递推关系式,状态转移矩阵、控制项系数矩阵和控制项矩阵分别为

在tk时刻的离散状态变量记为
(16)
系统的过程噪声项记为
wk=[wx,k-1wy,k-1wz,k-1wcx,k-1wcy,k-1we,k-1]T
(17)
忽略载体自身的漂角,载体和水的相对速度计算公式为
vw=Rb,nvb
(18)

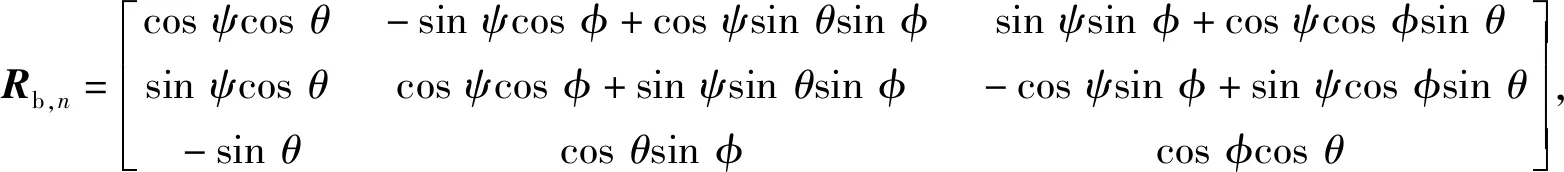
体坐标系相对导航坐标系的横滚角、纵倾角和航向角,通过姿态航向基准系统(Attitude Heading Reference System ,AHRS)测得。
采用水声信号传播时间为系统量测变量,扩展卡尔曼滤波量测方程如式(7)所示。hk表达式如式(8)所示。

(19)
所设计的新型水下单信标定位模型噪声项如式(17)所示,将6个噪声变量分为3组:(1)wx,k-1、wy,k-1、wz,k-1为在x、y和z方向的位置变化率噪声;(2)wcx,k-1和wcy,k-1为在x和y方向的海流变化率噪声;(3)we,k-1为ESV变化率噪声。假设这3组噪声变量相互独立,则噪声向量wk对应的离散方差矩阵Q′k为
(20)
式中:Q′p,k为wx,k、wy,k、wz,k的协方差矩阵(wx,k、wy,k、wz,k相关);Q′c,k为wcx,k和wcy,k的协方差矩阵(假设wcx,k和wcy,k不相关);Q′e,k为we,k的方差。

将系统状态变量x中的x、y、z进行离散,得:
(21)
海流速度在z轴方向无分量。


(22)
海流速度量测值与式(13)相同。
海流速度相应量测矩阵为
(23)
2 仿真分析
为验证所提出的6-SVM,利用该模型基于仿真数据进行数值模拟。基于定常的ESV情形,使用数值仿真数据对比5-SVM和6-SVM两种水下单信标定位模型。水声传播时间的量测噪声标准差设置为0.000 1 s;海流在x轴和y轴方向的量测噪声标准差均为0.000 1 m/s;深度计量测噪声标准差为0.000 1 m;真实声速设置为1 530 m/s,海流速度在x和y方向的分量均为恒定值0.3 m/s;水声信标每隔10 s发出1次水声信号,进行1次测距更新。采用扩展卡尔曼滤波进行航行器位置估计时,设置航行器在x、y、z方向的位置偏差均为10 m,初始ESV设为1 520 m/s。系统的随机动态噪声设置如下:假设vw在x、y、z方向的过程噪声标准差σwx、σwy、σwz均设置为0.1 m/s,vc在x、y方向的过程噪声标准差σcx和σcy均设置为0.01 m/s,设置ESV的过程噪声σe为0.1 m/s。当σe为0.1 m/s时,需要较长的时间才可以达到ESV真实值,但之后估计误差基本趋于0。在ESV设置为定常值时,选择较小的σe,可以得到较好的ESV仿真结果。σe为0.1 m/s时采用6-SVM进行扩展卡尔曼滤波对ESV的估计结果(见图2),500 s后估计结果趋于真实值且不再发散。

图2 ESV估计


图3 模型真实轨迹
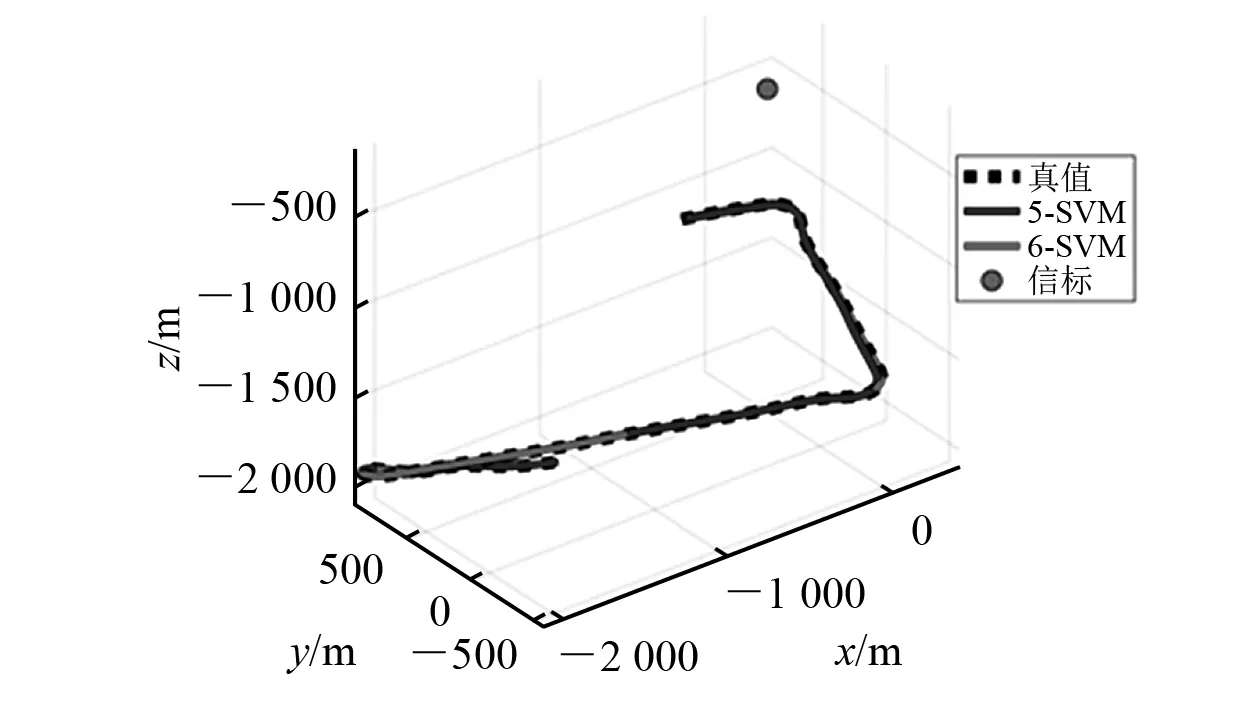
图4 航行器轨迹对比

图5 定位误差对比

图6 6-SVM测距新息和时延新息
3 结 语
建立的新型水下单信标定位6-SVM将水深作为状态变量,以水声传播时间和海流速度作为量测变量,利用扩展卡尔曼滤波进行航行器位置估算,建立相应的过程噪声模型。同时,基于仿真数据,进行6-SVM与5-SVM的数值仿真,对比2种模型的定位轨迹及定位误差。数值仿真显示新型单信标定位模型具有更好的ESV实时估计能力,且具有更高的定位精度。

