具有前向安全性的组密钥分发方案设计与实验分析

沈华，李继强，谢海涛，谌刚，张明武

（湖北工业大学计算机学院，武汉 430068）

0 引言

网络的飞速发展使得人与人之间的通信方式也不断地发生变化，从最初一对一的通信方式发展到一对多、多对多的组通信方式。特别是近年来受到新冠肺炎疫情的影响，几乎所有的会议、课程、聊天交流都转变为线上形式。腾讯会议、Zoom 会议、阿里钉钉等会议软件被广泛应用于线上教育和线上会议。网络的通信便捷性使得距离不再是阻隔，网络的开放性也使得保障组通信的安全成为了重中之重。特别是合法的组内通信成员也可能窃取其他成员的秘密数据，这就要求组通信方案的设计者不仅要考虑来自外部人员的攻击，也要防范来自内部恶意人员的攻击。一般情况下，安全组通信的通信成员会共享一个组密钥。组密钥实现了对通信信息的加密、解密以及对通信人员的身份验证。安全组通信必须有一个健壮的组密钥生成协议。目前主要有协商式和集中式两种组密钥生成协议。在协商式中，组密钥由组内全体成员共同“协商”决定。该类协议大多数是基于迪菲赫尔曼（Diffie-Hellman，DH）公钥方案演变来的［1］。在集中式中，不需要全组成员参与生成组密钥，但需要一个受信任的第三方——密钥生成中心（Key Generation Center，KGC）选择组密钥并安全分发给组内用户。

目前已有许多组密钥分发方法。Bohli［2］提出一个健壮的组密钥管理协议框架，该框架可在一个未经验证的点对点网络中提供针对内部恶意人员和主动攻击敌手的安全性。Chang 等［3］结合DH密钥交换协议和密钥封锁提出一种会议密钥分配协议，该协议使用插值多项式隐藏一些解锁信息。Katz等［4］提出了第1个完全可扩展的组DH 协议，该协议在标准模型下证明是安全的。Harn 等［5］利用Shamir［6］秘密共享方案提出一种基于KGC的组密钥分发协议，该协议使得只有授权的成员才能获得组密钥。Teng 等［7］提出一种基于身份加密的动态认证组密钥管理协议，通过利用已存储的成员信息有效地减少了成员的计算开销和通信消耗。Wu 等［8］提出一种不需要KGC 的新密钥管理范式。Harn等［9］提出一种使用多元多项式的密钥建立协议并给出了其在安全组通信和秘密共享的秘密重构中的应用。Harn等［10］提出无需可信第3 方的集中式组密钥分发协议。Jiao 等［11］提出一种基于秘密共享［12-13］的组密钥分发协议，逻辑上采用树形结构对组密钥进行管理。随后，Wu 等［14］提出基于对称二元多项式的轻量级认证组密钥管理协议，实现成员身份验证和组密钥生成。文献［15］中提出仅需逻辑异或操作的轻量级组密钥分发方案。文献［16］中以标识集广播加密方案（ISBE）［17］为基础构建用于GroupVPN的多播密钥分发协议。

本文对Harn等的方案［10］进行了改进，提出一种具有前向安全性的轻量级组密钥分发方案。

1 基本原理

1.1 对称二元多项式

有限域GF（q）中，t-1 阶多项式

式中：q为一个大素数；ai，j∈GF（q），i，j∈［0，t-1］。如果多项式系数均满足ai，j＝aj，i，那么该二元多项式是对称二元多项式。二元对称多项式f（x，y）有如下特点：对于GF（q）中的任意两个数xi和xj，f（x，y）一定满足f（xi，xj）＝f（xj，xi）。本文利用对称二元多项式生成的秘密份额建立用户对密钥。

1.2 前向安全性

组通信中的前向安全性是指在一个安全组通信过程中，即使用于产生会话密钥的主密钥不慎泄露了，也不会导致以前会话密钥的泄露。换句话说，主密钥的泄露无法保证当前通信的安全性，但是可以保证以前通信内容的安全性。

1.3 敌手模型

本文主要考虑以下两类敌手：

（1）内部敌手。即组通信中的合法用户试图获取其他用户的秘密信息，然后在组通信中伪装成该用户发起组通信。

（2）外部敌手。即通过窃听信道外部敌手获得用户发送和接收的信息以试图得到组通信中的组密钥，获取组内通信内容或者伪造通信请求以达到欺骗组内成员的目的。

本方案的安全性目标是实现具有前向安全性的组密钥分发，并能抵抗来自内部敌手的串谋攻击和外部敌手的被动攻击和欺骗攻击。

2 方案构成

本方案主要包括4 个阶段：系统初始化、二元多项式一致性检验、组密钥分发、组密钥获取。初始化阶段生成对称二次多项式和用户通信记录表，如图1 所示。

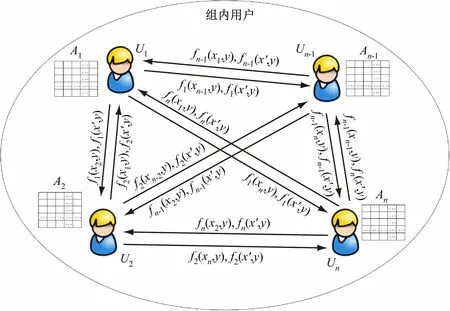
图1 系统初始化

一致性检验阶段中组内的每位用户对接收到的二元多项式进行一致性检验；组密钥分发阶段中组通信发起者在无KGC 的情况下实现具有前向安全性的组密钥分发；组密钥获取阶段中组通信其他用户从接收到的密文中获得用于组内通信的组密钥。组密钥分发与获取过程如图2 所示。

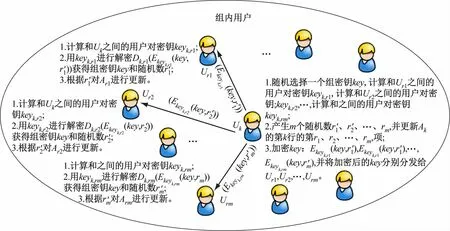
图2 组密钥的分发与获取

2.1 初始化阶段

设组内有n个用户U1，U2，…，Un，有n+1 个常数x1，x2，…，xn，x′是公开信息，其中xk是与用户Uk（k＝1，2，…，n）相关联的信息。以下为系统初始化的具体步骤。

步骤1用户Uk随机创建一个t次对称二元多项式：

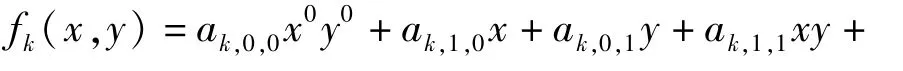
步骤2用户Uk通过安全信道将［fk（xl，y），fk（x′，y）］发送给用户Ul（l≠k；l＝1，2，…，n）。

步骤3用户Uk创建一个n×n的二维表Ak，其中所有元素均初始化为0。

2.2 二元多项式的一致性检验

每个用户需要检测2.1 节中其他用户随机生成的二元多项式是否是对称的t次二元多项式。

步骤1用户Uk首先验证收到的2（n-1）个一元多项式［f1（xk，y），…，fk-1（xk，y），fk+1（xk，y），…，fn（xk，y），f1（x′，y），…，fk-1（x′，y），fk+1（x′，y），…，fn（x′，y）］是否均是t次一元多项式，如果是，则执行下面的步骤，否则终止执行或重启初始化过程。

步骤2验证收到的2（n-1）个一元多项式是否均是由t次对称二元多项式生成的。具体验证步骤如下：

步骤2.1计算

步骤2.2计算

步骤2.3验证Fxk（x′）＝Fx′（xk）是否成立，如果成立，则继续执行后续步骤，否则终止执行或重启初始化过程。具体验证过程如下：根据式（1）、（2）和在1.1节中给出的对称二元多项式fk（x，y）定义，可以得到

式中：0≤i；j≤t且i≠j，根据对称二元多项式的定义可知，收到的2（n-1）个一元多项式均是由t次对称二元多项式生成的。

2.3 组密钥分发

假设用户Uk（k∈1，2，…，n）要向组内的m（m＜n）个用户发起组内安全通信，具有前向安全性的组密钥分发的具体步骤：

步骤1Uk计算他与用户Url（l＝1，2，…，m）之间的“用户对密钥”

步骤2用户Uk更新自己的二维表Ak。

步骤2.1生成m个随机数。

步骤2.2更新Ak的第k行

2.4 组密钥获取

用户获取组密钥步骤：

3 分析与比较

3.1 正确性分析

本方案初始化阶段后，组内每个用户拥有2（n-1）个由其他用户随机生成的t次对称二元多项式产生的一元多项式［f1（xk，y），…，fk-1（xk，y），fk+1（xk，y），…，fn（xk，y），f1（x′，y），…，fk-1（x′，y），fk+1（x′，y），…，fn（x′，y）］，这与其他n-1 个用户一一对应。根据对称二元多项式的特点，不需要用户间的交互，发起组通信的用户通过式（5）可以计算自己与其他用户之间的“用户对密钥”，组内其他用户通过式（6）也可以计算出发起用户与自己之间的“用户对密钥”。以用户Uk和为例进行说明，Uk通过式（5）得到的密钥

3.2 安全性分析

定理2本方案可以抗外部敌手的被动攻击。

证明外部敌手监听信道获得某一成员Ui得到了发送给用户Ul（l＝1，2，…，i-1，i+1，…，n）的一元多项式［fi（xl，y），fi（x′，y）］以及其接收来自其他用户的2（n-1）个一元多项式［f1（xi，y），f2（xi，y），…，fi-1（xi，y），fi+1（xi，y），…，fn（xi，y），f1（x′，y），f2（x′，y），…，fi-1（x′，y），fi+1（x′，y），…，fn（x′，y）］。由于二维表A由用户秘密存储，外部敌手在无法获得随机数的情况下或不知道二维表A的情况下，无法构造与用户在本地计算得到的“用户对密钥”，因此外部敌手无法得到用户对密钥，从而无法得到组通信密钥，本方案可以抵抗来自外部敌手的被动攻击。

定理3由组内用户创建并不断更新的二维表A保证了该方案具有前向安全性。

证明在计算“用户对密钥”时，发起组通信的用户Uk用其二维表中第k行第rl列的元素，随后Uk随机生成m个随机数，…用于更新其二维表第k行中对应位置上的元素，并将这些随机数与组密钥一起分发给对应的组成员。本轮更新的二维表将用于下一轮“用户对密钥”的生成。即使敌手获得了当前组通信中某两个用户之间的“用户对密钥”，由于“用户对密钥”是不断变化的，敌手也就无法获取他们之前的“用户对密钥”，使得该方案具有前向安全性。此外，除发起组通信用户之外的每个用户只会接收与自己对应的随机数，无法根据自己的二维表计算得到其他用户的“用户对密钥”，保证了当用户不在当前组时，他无法获得当前组以后的组通信密钥。

3.3 方案比较分析

本节从是否需要可信服务器、计算复杂度、存储要求等方面对本方案进行比较分析。在比较过程中，着重关注的是如何将组密钥分发给用户，由于不同协议使用了不同技术，因此，这里只关注顶层的比较。表1给出了比较的结果。

表1 相关协议比较

本文中提出的是一种具备前向安全性且不需要可信任KGC的方案，组通信的发起者需要分别执行n次多项式计算和n次常规加密，在组通信中将组密钥发送给n个用户，每个用户需要进行一次多项式计算和解密才能得到组密钥，同时还要更新通信记录表。本文提出的方案中并未涉及循环，系统只有加法和乘法计算，计算复杂度要求只取决于组通信中成员数量的多少，因此计算复杂度为O（n），在存储要求上由于每位用户只需要保存若干个一元多项式的系数和一个二维表A，因此存储要求为O（n2）。Harn 等［5］提出的方案使用带有RSA 模数的秘密共享将组密钥分发给所有用户，这个方案需要使用受信任的KGC，且KGC 需要使用多项式计算将组密钥分发给用户。用户也需要使用多项式计算来恢复组密钥。由于该方案使用了RSA模数，方案的计算复杂度为寻找RSA模数和执行多项式计算，因此计算复杂度为O（Lbp+n）（p为RSA模数），每位用户也只需要保存坐标点，因此存储要求为O（n）。文献［18］中提出基于秘密共享的组Diffie-Hellman协议，该协议不需要受信任的KGC 分发组密钥。组密钥由所有用户在使用秘密共享和DH方案的组通信中共同确定。该协议的主要问题是计算复杂度和通信复杂度，因为组密钥由所有用户共同确定，每个用户都需要计算DH 密钥并要与其他用户交换信息。该方案一共有3轮，前2 轮中每位用户都需要进行模幂运算，总的计算复杂度为O（2nLbe）（其中e为模幂运算上的指数），在存储要求上由于只需要保存公私钥对，因此为O（n）。Harn 等［10］提出使用对称二元多项式实现无第三方KGC的组通信中组密钥的分发，由于在该协议中用户之间使用的“用户对密钥”是固定不变的，导致一旦“用户对密钥”泄露，之前的通信信息就会泄露，并不具备前向安全性。该方案同样使用的是对称二元多项式，计算复杂度同样为O（n），在存储要求上由于用户需要存储的只有一元多项式系数，故为O（n）。文献［16］中为构建用于多节点通信的GroupVPN框架，提出了一种多播密钥分发协议用于实现多播组生成和组内密钥分发，该协议仍然需要系统生成主公钥和主私钥，然后生成组内用户的私钥。该协议由于以ISBE［17］为基础，在ISBE 中包含了多次指数级运算，计算复杂度为O（2n），由于每个用户只要保存自己的私钥，因此总的存储要求为O（n）。

3.4 组密钥分发仿真实验分析

本节通过仿真表明，本文所提方案的正确性和可行性。仿真主要包括：系统初始化与一致性检验；组密钥的分发；组密钥的安全获取。仿真选择CPU时间和存储空间消耗作为评价指标，选择AES-256 实现方案中的信息加密。测试平台配置：操作系统为win10，CPU为i5-4590，8GB 内存。分析讨论的是，通信群组规模大小n和多项式最高次数t对上述3 个过程所需CPU时间的影响。

图3 给出了在不同多项式最高次数t随着群组规模n的增大，本方案初始化与一致性验证阶段所花费的CPU时间的增长情况。群组规模的不断增大，用户间交互次会激增，初始化与一致性验证阶段需要花费的时间也会增加。结果表明，随着群组规模增加，本方案初始化与一致性验证阶段所花费CPU 时间基本呈线性增长。

图3 系统初始化时间开销

图4 给出了在不同多项式最高次数t随着群组规模n的增大，组密钥分发阶段所花费的CPU时间的增长情况。结果表明，即使用户规模达到了一定的程度，本方案仍能够在很短时间内完成对所有用户的组密钥分发过程。

图4 组密钥分发时间开销

图5 给出了在不同多项式最高次数t随着群组规模n的增大，组密钥安全获取阶段所花费的CPU时间的增长情况。结果表明，随着群组规模的增加，安全获取密钥阶段所花费的CPU时间基本呈线性增长，但仍然能够在秒级内处理完成。

图5 组密钥的获取时间开销

图6 给出了在不同多项式最高次数t随着群组规模n的增大，每个用户存储开销的增长情况。实验结果表明，随着群组规模增加，用户存储开销呈线性增长。相较于当下设备存储空间的几十GB 而言，所需的几十KB空间占比几乎为0，因此本方案十分适合各种设备使用。

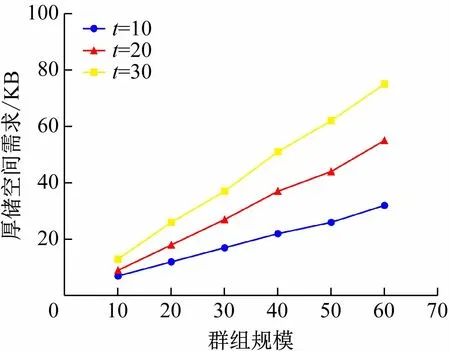
图6 存储需求

4 结语

受新冠疫情影响，很多会议都变为线上形式，保证安全的通信环境变得至关重要。为实现安全组通信，需要用组密钥对通信内容进行加解密。本文解决的关键问题是如何在无可信KGC 的情况下进行具有前向安全性的组密钥分发。所提方案让每次发起组通信的用户充当KGC的角色，负责随机选择本次组通信的组密钥，并利用与其他用户之间的用户对密钥实现对组密钥的安全分发。同时随机生成用于更新用户对密钥的随机数，以实现前向安全性。此外，提出的组密钥分发方案只需要较少的计算量和存储量，非常适用于通过手机、平板电脑等资源有限设备进行组内通信的用户。