基于增强慢特征分析的控制系统振荡智能检测

韩涛，姚 维

（浙江大学电气工程学院，杭州 310027）

0 引言

控制系统是现代工业的核心，广泛存在于钢铁冶炼、火力发电等场景，系统的稳定运行至关重要［1-3］。然而，受工作环境、自身材料或结构老化、参数设定不合理等因素影响，控制系统往往会出现缓慢的性能退化直至失效，进而引发生产事故。在众多性能退化表现中，振荡最为常见，其会对控制回路性能产生不利影响，并可能迫使系统长期在次优条件下运行［4-5］，因此，控制系统振荡的智能检测技术的研究具有十分重要的意义。

现有的振荡智能检测方法主要分为信号分析法和统计学习法。信号分析法主要包括误差积分法［6］、小波分析法［7］、离散傅里叶分解［8］、经验模态分解［9］等，该类方法通常需要对数据进行在线处理，且易受噪声影响，不利于振荡的实时检测；统计学习法包括相对变化分析法［10］和慢特征分析法（Slow Feature Analysis，SFA）［11-14］，该类方法可通过离线建模获取模型特征，有效降低在线应用的复杂度。其中，SFA 虽然能有效地从数据中解耦出系统的主要变化趋势和波动特征，识别系统的振荡信号，但SFA 为线性统计模型，对于非线性系统，模型检测准确率比较低。

针对上述问题，本文提出了增强慢特征分析方法（Feature-Enhanced SFA，FESFA）来实现非线性系统的振荡检测，在原有SFA 方法的基础上，引入增强特征来处理非线性变量，使其更好地捕捉控制系统的时序特性，提高振荡现象的检测准确度。同时，仿真实验结果证实所提出方法能有效地提升振荡检测的准确率。

1 慢特征分析

慢特征分析是一种针对于多元时序信号的特征提取方法，其从原始数据中提取随时间缓慢变化的特征来描述时序动态性。

1.1 慢特征分析的建模与求解

对于N维输入信号（t）＝［x1（t），…，xN（t）］Τ，SFA旨在寻找一系列线性映射w1，…，wN，使得输出信号y1（t），…，yN（t）变化尽可能缓慢，其中yj（t）＝x（t）（j＝1，2，…，N）。具体优化目标可以写为［12-13］

式中：i、j为序列数，t为时间，N为样本总数；〈·〉t算子表示对尖括号中变量在各时间点上的取值取平均。

为求解上述优化问题，需要对x（t）作去中心化处理，即令x（t）中各信号分别减去各自的均值；将yj（t）＝x（t）带入式（1），得：

可见，原问题已经转变为简单的广义特征值分解问题，分解得到的特征向量即为所求线性映射w1，…，wN。

1.2 基于慢特征的变化速率指标

对于求得的特征y1（t），…，yN（t），将其按由慢到快顺序排列，并将其划分为较慢特征ys()t＝［y1（t），和较快特征yf(t)＝［yn+1（t），…，yN（t）］Τ，其中n为组份划分数目，一般可以选定为样本总数N的80%。较慢特征表征了多元信号中的主要变化趋势，而较快信号则携带了原信号中快速波动成分的信息。基于SFA 的振荡检测模型建立了2 个变化速率指标ds和df来量化系统的波动程度：

式中：ds表示慢速率指标；df表示快速率指标；var（·）表示求方差运算。由于SFA 对特征的缓变进行约束，因此ds和df取值越大，说明系统内存在异常快速波动的可能性越大，从而可认为系统发生了振荡。一般情况下，可以根据正常数据的ds和df取值分布设定检测阈值，在线检测时，一旦任一变化速度指标超出该阈值，则认为系统中出现了振荡现象。本文中的阈值设定规则为

式中：c（ds）和c（df）分别为ds和df统计量的检测阈值。

2 增强慢特征分析模型设计方法

系统中的测点间同时存在线性与非线性关系，对于线性相关的时间序列变量组｛x1（t），…，xk（t）｝，其一阶时间差分｛（t），…，（t）｝同样线性相关，因此可以找到1 个线性映射，使得这组变量一阶差分的线性组合取值尽可能趋近于零；对于非线性相关的变量组，则无法依靠线性映射来拟合变量及其一阶差分间的关系。由式（1）可知，SFA 模型的优化目标可以转化为寻找线性映射使得系统中变量一阶差分的线性组合取值尽可能趋近零。因此，在SFA 提取慢特征时，会倾向于为线性相关的变量分配数量级较大的权重从而使他们的线性组合呈现缓变特性，而对于非线性变量则会分配数量级较小的权重，弱化其在慢特征中的表现而实现缓变目标。为解决这一问题，提出基于增强特征的SFA方法来解决非线性问题，首先根据SFA的模型参数识别出非线性变量，再引入非线性回归模型对非线性变量进行拟合，并将拟合结果作为增强特征，从而使得模型能够自动将非线性关系转化为线性关系，便于SFA处理。

2.1 基于神经网络的非线性回归建模

在FESFA模型中，需要训练非线性回归模型来获取非线性变量的拟合结果。多层全连接神经网络［15］结构灵活、精准度高，尤其擅长于处理数据中的非线性关系，因此选择神经网络作为回归模型。对于1 个回归任务中所包含的自变量x ＝［x1，…，xN］Τ及待预测值p，神经网络在输入层接收自变量信息，在每个隐藏层对输入数据进行非线性变换得到隐藏特征，最终在输出层对隐藏特征进行线性变换得到预测值，通过最小化与p间的差距来优化网络参数。具体而言，设第l个隐藏层的输入为fl，则神经网络按照如下形式对其进行非线性变换：

式中：L为总隐藏层数；Kl-1、bl-1和δ 分别为第（l-1）个隐藏层的权重矩阵、偏置向量和非线性激活函数。通常可选择修正线性单元（Rectified Linear Unit，ReLU）作为非线性激活函数，其表达式为

对于输出层中的线性变换，只需在式（8）的基础上去掉非线性激活函数即可，即：

式中，Ko与bo为输出层的权重矩阵及偏置向量。最终，整个神经网络的优化目标为

由于神经网络结构灵活，在FESFA 模型中，只需调整相应的输入输出来训练神经网络，即可获取相应的非线性回归模型。

2.2 总体建模与应用流程

考虑到变量间可能存在多组非线性关系，所提出模型中设计了一种迭代求解策略，在每轮迭代中自动识别非线性信号并利用上述的神经网络模型对其进行拟合来获取增强特征，通过判断引入的特征对模型性能是否有提升作为模型的迭代终止条件。具体建模流程如下：

输入N维输入信号x(t)＝［x1（t），…，xN（t）］Τ，非线性神经网络回归器r。

步骤1初始化回归器集合R以及待拟合非线性变量索引集合I为空集，定义变化速率判定阈值为D。

在每轮迭代过程中，本文提出的FESFA模型通过分析SFA模型的权重向量，寻找出非线性度最高（即与其他变量线性相关程度最低）的变量xi（t），采用神经网络回归模型ri得到xi（t）的拟合结果（t），并添加到原数据中。由于拟合结果（t）与xi（t）之间必定存在较强的线性相关关系，因此上述操作本质上提升了变量间的线性相关强度，便于SFA求解线性映射关系来实现缓变的优化目标。此外，ds统计量能够表征特征的缓慢程度，若新引入的增强特征有利于提升模型性能，则模型特征变化将更加缓慢，使得ds下降。故通过ds指标下降与否即可判断是否需要停止迭代。

建立好FESFA模型后，利用式（6）计算统计量的检测阈值c（ds）和c（df），并将其应用在线振荡检测，其步骤如下：

输入在线样本

步骤1利用建模阶段获取的R中每个回归器ri拟合出I中记录的所有非线性变量的估计值；

步骤2将作为增强特征与原样本xn组合；

步骤3用建模阶段保存的SFA 模型M进行特征提取，并计算变化速度指标ds和df；

步骤4判断ds和df是否超过相应的检测阈值，如未超过，则判断系统中不存在振荡现象；若二者任一超过阈值，则判定系统中存在异常振荡。

3 实验验证

3.1 实验设计

在CPU（Intel（R）Core（TM）i7-9750H CPU ＠2.60 GHz）硬件环境中，采用Python3.7，利用其数值计算工具库NumPy（Numerical Python）1.92.2 以及机器学习工具库scikit-learn0.19.2 进行控制系统仿真与算法实现。

构建若干非线性信号｛u1（t），u2（t），s1（t），s2（t），s3（t）｝，验证所提出FESFA模型的有效性：

式中：u1（t）和u2（t）为2 个独立的白噪声输入，服从均值为0，标准差为1 的高斯分布；｛s1（t），s2（t），s3（t）｝为输出信号，5 个信号共同模拟了1 个二输入三输出的控制系统。由式（12）可知，信号｛u1（t），u2（t），s1（t），s2（t）｝间具有线性关系，而s3（t）则与其他信号具有非线性关系。按照上式的生成机制，共生成1 500个测量样本，其中前1 000 个为正常数据，图1 中蓝色所示，第1 001 到1 500 个样本点中，在信号s3（t）上叠加1 个幅值为0.3 的高频正弦信号来模拟振荡，图1中红色所示。将生成的前500 个样本用于训练，后1 000 个样本用于测试模型性能，各信号变化曲线如图1所示，可以看出即便是在加入振荡信号后，信号s3（t）上的异常趋势也并不明显，这为振荡检测模型带来挑战。

图1 实验信号变化曲线

3.2 实验结果分析

设定误报率（False Alarm Rate，FAR）和检测准确率（Detection Accuracy，DA）2 个指标来评估所提出FESFA方法的性能，其中：FAR 为测试数据中被误判为振荡的正常样本占所有正常样本的比例，其值越低则模型性能越好；DA 为测试数据中被模型正确判定为振荡的样本占所有振荡样本的比例，其值越高则模型性能越好。选取相对变化分析法和SFA 法作为对比，各模型的振荡检测性能指标如表1 所示。可见各模型的FAR 指标并无显著差异，但所提出FESFA 模型的DA指标显著高于两个对比模型，这是由于本实验案例中引入的振荡被叠加在信号s3（t）上，而s3（t）恰与输入信号u1（t）和u2（t）具有显著的非线性关系，这是两个对比模型所无法处理。相反，所提出的FESFA模型能够引入非线性增强特征来处理非线性变量，因此检测准确率显著提升。

表1 各模型振荡检测性能指标

为进一步验证所提出模型的可靠性，图2 所示为FESFA模型在第1 轮迭代中所求解的第1 个慢特征权重系数绝对值的可视化图，由图可知，非线性信号s3（t）的权重明显低于其他信号，这说明FESFA模型对系统中的非线性信号有了感知能力。图3 所示为FESFA中非线性回归模型对所识别出的非线性信号的拟合结果，对于正常数据，拟合结果与原始信号非常接近，而对于振荡信号，拟合结果与原信号具有明显差异，这说明FESFA中所设计的非线性拟合机制能够有效捕捉异常振荡。此外，图4 为FESFA模型所提取的慢特征信号，由图可知，在振荡发生前信号变化相对较缓，但在振荡发生之后出现了频繁大范围波动，验证了所提出方法确实能够通过缓变程度，即变化速率来识别系统内的异常振荡信号。

图2 第一轮迭代各信号权重绝对值示意图

图3 非线性信号的拟合结果

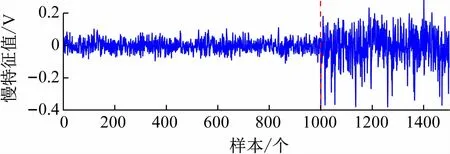
图4 提取的慢特征信号（红色虚线代表振荡起始时刻）

4 结语

针对非线性系统，传统振荡检测方法准确率较低的问题，提出基于增强特征的SFA 方法，通过对传统SFA方法的权重系数进行解析并引入非线性回归模型，实现非线性信号的自动识别与拟合，赋予SFA 处理非线性特性的能力。在二输入三输出的非线性仿真系统上进行振荡检测实验，最终的误报率和检测精度分别为4.37%和79.4%，相比于两种经典振荡检测方法（相对变化分析和慢特征分析），本方法误报率平均降低0.625%，检测精度平均提高36.7%。实验结果表明，所提出方法在非线性控制系统的振荡检测任务中相比于传统方法准确率得到显著的提升，且可以通过分析模型运算过程的中间结果来解释模型的有效性，进一步验证模型的可靠性。