数学问题解答

2021年9月号问题解答

(解答由问题提供人给出)

(山西省临县一中 李有贵 033200)

2622如图，四边形ABOC中，AB=AC，OB=BC=CO，∠A=80°，点M在BC上，满足∠CAM=20°．以O为圆心，OB为半径作圆交AM于Q，求证∠QBC=10°.

(湖北省公安县第一中学 杨先义 434300)

证明显然⊙O与线段AM的交点Q唯一存在，且∠BQC=150°.

下面用同一法证明结论.

在线段AM上取点Q1，Q2，使

∠BCQ1=20°，∠CBQ2=10°，

由已知可得∠ABC=∠ACB=50°.

设△ABC的外接圆直径为1，

由正弦定理

BC=sin80°，AB=AC=sin50°.

而BC=BM+MC=sin80°，

在△AMC和△ABM中，由面积关系可得

⟺sin30°sin60°sin10°=sin220°sin40°

再由Q的唯一性即得Q′与Q重合，

所以∠QBC=10°.

2623设a≥b≥c≥0,a+b+c=3,求证:

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

证明因为a≥b≥c≥0,

所以(a-b)(b-c)(a-c)≥0,

即a2b+b2c+c2a≥ab2+bc2+ca2.

于是，结合舒尔不等式

a3+b3+c3+3abc

≥a2b+b2c+c2a+ab2+bc2+ca2，

得a3+b3+c3+3abc≥2(ab2+bc2+ca2).

从而27=(a+b+c)3

=a3+b3+c3+6abc+3(a2b+b2c+c2a)+

3(ab2+bc2+ca2)

≥a3+b3+c3+6abc+6(ab2+bc2+ca2)

≥3abc+8(ab2+bc2+ca2),

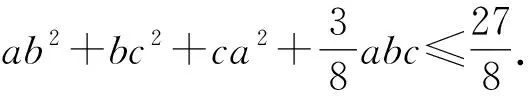
2624在Rt△ABC中，点D为直角边BC的中点，点E在斜边AB上且满足AE=CD，点F为线段ED的中点，证明：∠CAF= ∠DEB.

(河南辉县一中 贺基军 453600)

证明如图，延长AF到点H，且使FH=AF，在线段EB上截取EG=AE，连接HB，HC，HD，HE，HG和AD.由AF=FH，EF=FD知四边形ADHE为平行四边形，由EG=AE=DH知四边形EDHG为平行四边形，由DH=AE=CD=DB知△BCH为直角三角形.设∠BCH=θ.

由AB∥DH得∠ABD=∠BDH= 2θ，

由∠BHC= 90° 得∠CBH= 90° -θ，

因此 ∠ABH= 2θ+ (90° -θ)

=90° +θ= ∠ACH.

设BC=a，AC=b，AB=c，HB=m，HC=n.在△ACH中，

AH2=AC2+CH2-2AC·CH·cos∠ACH

另一方面，在△ABH中，

b2=c2-a2，n2=a2-m2代入上式得

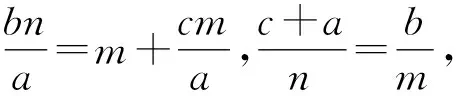
因c-a=AB-CB=AB-AG=GB，

从而可知 △ACH∽△GBH，

于是 ∠CAF=∠BGH=∠DEB.

(安徽省六安第二中学 陶兴红 237005)

解易知

且 sinA+sinB+sinC

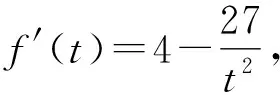
2021年10月号问题

(来稿请注明出处——编者)

2626如图，D、E、F分别是三角形ABC三边(或延长线)上的点，满足∠ADC=∠BEA=∠CFB，直线AD、BE、CF两两交于点L、M、K，点H是△ABC的垂心. 求证：点H是△LMK的外心.

(浙江省慈溪实验中学 华漫天 315300)

2627在△ABC中，已知外心为O，内心为I，旁心分别为Ia,Ib,Ic，R为外接圆半径，求证：

(1)

(河南质量工程职业学院 李永利 467001)

2628已知正实数a,b,c满足

(浙江省海盐县元济高级中学张艳宗 314300；北京航空航天大学图书馆 宋庆 100191)

2629设双曲线C的两焦点为F1、F2，两准线为l1、l2，过双曲线上一点P，作平行于F1F2的直线，分别交准线l1、l2于M1、M2，直线M1F1与M2F2交于点Q，则：P、Q、F2、F1四点共圆.

(江西省都昌县第一中学 刘南山 332600)

2630在ABCD中，M为对角线AC的中点，E、F分别在边AB、BC上，满足∠EMA=∠FMC=∠ADC,O1、O2、O3、O4分别为△EMA、△EBF、△FMC、△ADC的外心.

求证：四边形O1O2O3O4是平行四边形.

(陕西省兴平市教研室 吕建恒 713100)