对一个向量恒等式的反思
杨贵武
(广东省深圳市高级中学 518040)
近年来,用向量研究三角形“五心”的文章比较多.而研究勃罗卡点,特别是生成向量恒等式的,却很少.《数学通报》刊发的《一个奇妙的向量恒等式》[1]一文,介绍了下面恒等式,并加以证明,同时给出了该恒等式的若干应用.

图1
如图1,已知P是△ABC内部一点,且满足∠PAB=∠PBC=∠PCA=α,则称α为勃罗卡角,点P为勃罗卡点,则有

文[1]证明上述恒等式用到两个不常见的引理.能否不用引理,直接证明上述恒等式?另外,能否基于该恒等式,得到更多的结论.一直思考却没有突破,直到《数学通报》连载了张景中院士和彭翕成博士关于点几何的论文[2~4],让笔者获益匪浅,茅塞顿开.
简单地说,可以将点几何理解成向量的简写版本.


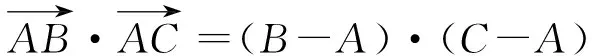
=(A-B)·(A-C).
于是

=(A-B)·(A-P)+(B-C)·(B-P)+(C-A)·(C-P)
=A2+B2+C2-A·B-B·C-C·A.
而

=(A-B)·(A-C)+(B-C)·(B-A)+(C-A)·(C-B)
=A2+B2+C2-A·B-B·C-C·A.
如果不习惯点几何这种记号,也容易改成向量形式,即


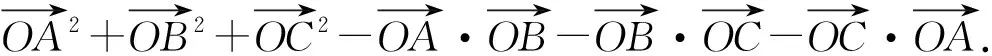


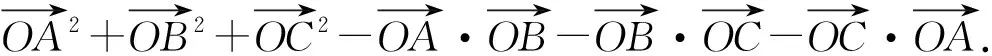
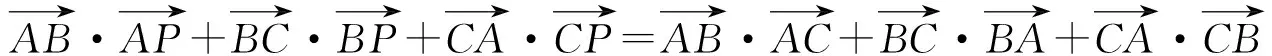
下面给出该恒等式的几点应用.
应用1如图1,设点P是勃罗卡点,则cotα=cotA+cotB+cotC.



=2S△ABPcotα+2S△BCPcotα+2S△CAPcotα
=2cotα(S△ABP+S△BCP+S△CAP)
=2S△ABCcotα;

=2S△ABCcotA+2S△ABCcotB+2S△ABCcotC,
=2S△ABC(cotA+cotB+cotC);
根据恒等式①可得
2S△ABCcotα=2S△ABC(cotA+cotB+cotC),即cotα=cotA+cotB+cotC.
应用2如图2,设点P是内心,则
=(a+b+c)(cotA+cotB+cotC).


=2S△ABCcotA+2S△ABCcotB+2S△ABCcotC,
根据内心的性质可得[5]
S△ABP:S△BCP:S△CAP:S△ABC=c:a:b:(a+b+c),
结合恒等式①可得
=(a+b+c)(cotA+cotB+cotC).

图2
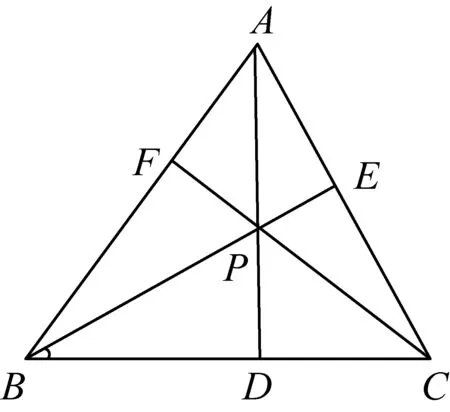
图3
应用3如图3,设点P是垂心,则
tanAtanBtanC=tanA+tanB+tanC.

=2S△ABPtanB+2S△BCPtanC+2S△CAPtanA;

=2S△ABCcotA+2S△ABCcotB+2S△ABCcotC,
根据垂心的性质可得[5]
S△ABP:S△BCP:S△CAP:S△ABC
=tanC:tanA:tanB:(tanA+tanB+tanC),
结合恒等式①可得
tanCtanB+tanAtanC+tanBtanA
=(tanA+tanB+tanC)(cotA+cotB+cotC),

即 cotA+cotB+cotC
推出经典恒等式
tanAtanBtanC=tanA+tanB+tanC.
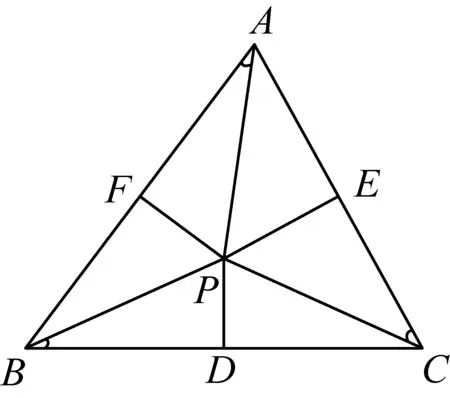
图4
应用4如图4,设点P是外心,则2(sin2A+sin2B+sin2C)=(sin2A+sin2B+sin2C)(cotA+cotB+cotC).
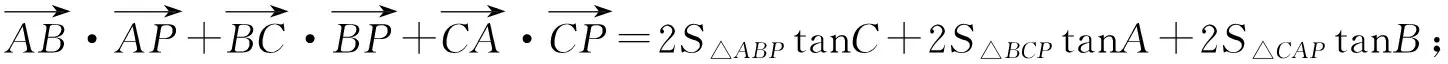

=2S△ABCcotA+2S△ABCcotB+2S△ABCcotC,
根据外心的性质可得[5]
S△ABP:S△BCP:S△CAP:S△ABC
=sin2C:sin2A:sin2B:(sin2A+sin2B+sin2C),
结合恒等式①可得
tanAsin2A+tanBsin2B+tanCsin2C
=2(sin2A+sin2B+sin2C)
=(sin2A+sin2B+sin2C)(cotA+cotB+cotC).
应用2-4所得三角恒等式,虽然是在P取某些特殊位置时得到,但容易验证,这些结论的成立与P无关,是恒等式.至此我们就从一个向量恒等式出发,探索得到了一些新的三角恒等式,完成了一次有意义的探索之旅.

