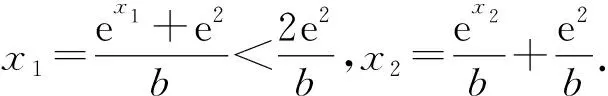突出“一核”功能 考查“四层”内容落实“四翼”要求
——2021年高考数学试题评析
张 健
(北京市丰台区第二中学 100071)
2021年的高考是按照《中国高考评价体系》进行命题的第二次高考,同时也是江苏、湖南、湖北、河北、广东、福建、辽宁、重庆八省(市)新高考综合改革落地的首考,全国有新高考Ⅰ卷、新高考Ⅱ卷、北京卷、上海卷、天津卷、浙江卷、全国乙卷(文、理科各一套)、全国甲卷(文、理科各一套)共计十套数学试卷.综合来看,这些试卷都很好地落实了“立德树人、服务选才、引导教学”的核心功能,使得新高考综合改革的成功实践又向前迈出了坚实的一步.
1 以核心价值为引领
根据高中数学课程标准、高校人才选拔要求和考试测评的规律,高考评价体系将所考查的素质教育目标提炼为“核心价值、学科素养、关键能力、必备知识”四层考查内容[1].
“核心价值是指即将进入高等学校的学习者应当具备的良好政治素质、道德品质和科学思想方法的综合,是在各学科中起着价值引领作用的思想观念体系,是其在面对现实的问题情境时应当表现出的正确的情感态度和价值观的综合.”[2]2021年的数学试卷凸显了“立德树人、全面发展”的核心理念,重视对学生的政治立场和思想观念、世界观和方法论、道德品质和综合素质等方面核心价值的引领.
1.1 厚植爱国情怀,践行核心价值观
2021年高考数学能将重大的社会热点事件有机融入试题,通过设计真实问题,展示我国发展的伟大成就,对学生进行坚定理想信念、厚植爱国情怀、提升品德修养、培养奋斗精神、践行社会主义核心价值观等核心价值的引领.
例1(北京卷第18题)为加快新冠肺炎检测效率,某检测机构采取“k合1检测法”,即将k个人的拭子样本合并检测,若为阴性,则可以确定所有样本都是阴性的;若为阳性,则还需要对本组的每个人再做检测. 现有100人,其中有2人是感染新冠病毒的患者.
(Ⅰ)①若采用“10合1检测法”,且两名患者在同一组,求总检测次数;
(Ⅱ)若采用“5合1检测法”,检测次数Y的期望为E(Y),试比较E(X)和E(Y)的大小(直接写出结果).
分析:本题对阅读理解能力要求很高.在(Ⅰ)①中,分成10组要检测10次;由于2名患者在同一组,这组的每个人还都要做检测,因此共需要做10+10=20次检测.

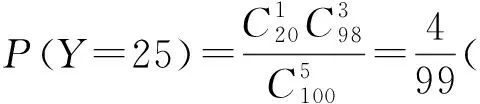
本题以新冠病毒的“k合1”核酸检测技术为背景,让学生体会概率统计知识在大规模排查新冠感染者的实际问题中的应用,体会数学的应用价值.由于我国成功地控制住了新冠疫情,当个别地方出现散发病例时,能够使用“k合1检测法”进行大规模的快速检测,而对于疫情失控的国家是无法使用该法的.真实的问题情境展示了我国科学防疫的成果,有利于增强学生民族自豪感,培养爱国主义精神.
另外,新高考Ⅰ卷第18题是以知识竞赛为题材,宣传“一带一路”国家战略,考查随机变量的分布与均值等内容;全国甲卷理科第8题,是以“2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m)”为背景设计的解三角形问题,这也是我国继1975年、2005年之后,第三次公布这一地球最高峰的海拔数据,展示了中国的登山能力和测量水平;全国乙卷理科第6题,是以北京冬奥会志愿者服务为题材设计的排列组合问题,北京也是世界上唯一一个举办过冬、夏两季奥运会的城市,彰显了祖国的辉煌成就和实力.这些试题从不同角度对学生进行爱国主义教育,践行社会主义核心价值观.
1.2 采撷古今经典,弘扬传统文化
2021年的高考试卷中,还有许多用“经典”传承数学文化的试题,这些“经典”是人类文明的根脉,是立德树人的红色基因,它承载着思想与文化,是对学生弘扬民族精神、培养爱国情操,提高审美情趣、培育劳动精神,健全完善人格、锤炼意志品质等核心价值的引领.
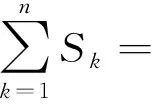
分析:设对折次数为n.
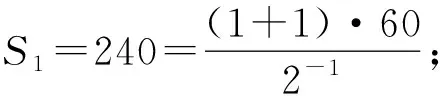
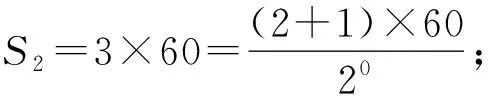
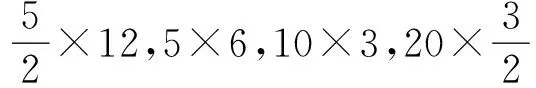



本题以我国民间剪纸艺术为背景,考查归纳推理和数列求和等内容,弘扬中国传统文化.
另外,北京卷第6题,是以党旗为背景设计的数列问题,向学生传承红色文化,赓续红色基因,又有喜迎建党100周年之蕴意;浙江卷第11题,是以“赵爽弦图”为题材设计的面积计算问题,三国时期吴国的赵爽利用弦图证明了勾股定理,这比古希腊数学家毕德哥拉斯给出的证明早了550多年;全国乙卷理科第9题,是以“魏晋时期刘徽撰写的《海岛算经》中的第一题:测海岛的高”为题材,考查相似三角形、合分比性质等内容;上海卷的第19题以企业利润为背景,考查“增长率”问题,等等.这些试题都从不同角度引导学生弘扬传统文化,落实立德树人的根本任务.
1.3 重视数学应用价值,倡导科学发展理念
现代数学在促进科学技术和其他学科发展、社会生活与生产应用、人类文化与社会文明进步等各个领域都有巨大价值和独特功能,这是由数学的研究对象及其所具有的属性和特征决定的.2021年高考的一些试题,是让学生通过数学应用,理解国家的方针政策,倡导科学发展的理念.
例3(新高考Ⅱ卷第21题)一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代,……,该微生物每代繁殖的个数是相互独立的且有相同的分布列. 设X表示1个微生物个体繁殖下一代的个数,P(X=i)=pi(i=0,1,2,3) .
(Ⅰ)已知p0=0.4,p1=0.3,p2=0.2,p3=0.1,求E(X);
(Ⅱ)设p表示该种微生物经过多代繁殖后临近灭绝的概率,p是关于x的方程:
p0+p1x+p2x2+p3x3=x的一个最小正实根,求证:当E(X)≤1时,p=1;当E(X)>1时,p<1;
(Ⅲ)根据你的理解说明(Ⅱ)问结论的实际含义.
分析:(Ⅰ)E(X)=0×0.4+1×0.3+2×0.2+3×0.1=1.
(Ⅱ)由方程
p0+p1x+p2x2+p3x3-x=0(x>0),
因为p是关于x的方程p0+p1x+p2x2+p3x3=x的一个最小正实根,且0 所以0 f(x)=p0+p1x+p2x2+p3x3-x(0 则f′(x)=p1+2p2x+3p3x2-1, f″(x)=2p2+6p3x≥0, 所以f′(x)在(0,1]上单调递增. ①当E(X)=p1+2p2+3p3≤1时, 有f′(x)≤f′(1)=p1+2p2+3p3-1≤0, 从而f(x)在(0,1]上单调递减, 所以f(x)在(0,1]上至多有一个零点. 又p0+p1+p2+p3=1, 所以f(1)=p0+p1+p2+p3-1=0, 即有p=xmin=1; ②当E(X)=p1+2p2+3p3>1时, 注意到f′(0)=p1-1<0, f′(1)=p1+2p2+3p3-1>0, 所以存在唯一的x0∈(0,1),使得f′(x0)=0. 从而,当x∈(0,x0)时,f′(x)<0; 当x∈(x0,1]时,f′(x)>0. 即f(x)在(0,x0)上单调递减,在(x0,1]上单调递增. 又f(0)=p0>0,f(x0) 所以p=xmin=x1<1. 综上,当E(X)≤1时,p=1;当E(X)>1时,p<1. (Ⅲ)当1个微生物个体繁殖下一代的期望小于等于1时,这种微生物经过多代繁殖后临近灭绝;当1个微生物个体繁殖下一代的期望大于1时,这种微生物经过多代繁殖后还有继续繁殖的可能. 本题属于概率综合题,第(Ⅱ)(Ⅲ)问分别是概率与函数、期望与决策综合问题,折射出科学制定人口生育政策问题:当实行“一对夫妻一个孩”的生育政策时,必然会出现人口锐减、老龄化等问题,这也是国家相继出台“二胎”“三胎”政策的原因所在.数学的科学价值是独特的,应用价值是广泛的,文化价值是多维的,审美价值是丰富的,这些价值是引导学生理性分析问题、学会科学决策、树立正确价值观的重要资源. 全国甲卷理科第4题、文科第6题,是以青少年视力这个现实热点问题为题材,考查指数与对数运算及其估算内容,引导学生锻炼身体、保护好视力;全国甲卷理科第17题和全国乙卷文、理科第17题,都是以工厂生产为背景,考查用样本估计总体、独立性检验等内容,引导学生关注生产、热爱劳动.这些试题对引导教育要落实“五育并举”方针,关注学生德智体美劳全面发展,起到积极的促进作用. 总之,数学学科虽然在考查“核心价值”方面不像人文学科那样鲜明、深入,但从2021年的数学试卷可以看出,在考查“品德修养、奋斗精神、责任担当、健全情感、劳动精神”等方面都进行了创新探索与尝试,积极引导学生践行社会主义核心价值观,树立高远志向,培育敢于担当、刚健有为、自强不息、乐观向上的人生态度. “学科素养是指即将进入高等学校的学习者在面对生活实践或学习探索问题情境时,能够在正确的思想价值观念指导下,合理运用科学的思维方法,有效整合学科相关知识,运用学科相关能力,高质量地认识问题、分析问题、解决问题的综合品质.”[3]综观2021年高考数学试题,重视对“数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析”[4]六个数学核心素养的考查,既有对每个素养独有的内涵、特指的价值取向的考查,更有对六个数学素养整合性和综合性的考查,“以学科素养为导向”的考查理念清晰、强烈! A.a C.b 本题中用变量x表示三个不同式子的关系需要数学抽象素养,发现a>b需要数学直观素养,构造函数f(t)比较a与c的大小需要数学建模、数学运算素养,多个素养的整合才能完成解题. (Ⅰ)求C的方程; 本题对六个核心素养的要求都很高,既考查每个素养鲜明的特征和独特的内涵,同时又考查六个核心素养的整合性和综合性(因为六个核心素养是彼此关联的:数学运算是逻辑推理,数据分析是特殊的数学建模,它们组成一个有机的整体,相互交融,学生在运用数学知识解决问题的过程中,表现出整合性和综合性的特点). “关键能力是指即将进入高等学校的学习者在面对与学科相关的生活实践或学习探索问题情境时,高质量地认识问题、分析问题、解决问题所必须具备的能力.”[5]根据高考的特征,高考评价体系“确立了符合考试评价规律的三个方面的关键能力群:一是以认识世界为核心的知识获取能力群;二是以解决实际问题为核心的实践操作能力群;三是涵盖了各种关键思维能力的思维认知能力群.”[6]根据数学学科特点和考查功能,2021年的试题重点考查了阅读理解、信息整理、批判性思维、语言表达等关键能力. 例6(新高考Ⅱ卷第4题)卫星导航系统中,地球静止同步轨道卫星的轨道位于地球赤道所在平面,轨道高度为36000km(轨道高度指卫星到地球表面的最短距离),把地球看成一个球心为O,半径为r=6400km的球,其上点A的纬度是指OA与赤道所在平面所成角的度数,地球表面能直接观测到的一颗地球静止同步轨道卫星的点的纬度的最大值记为α,该卫星信号覆盖面的地球表面积S=2πr2(1-cosα)(单位km2),则S占地球表面积的百分比为( ) A.26% B.34% C.42% D.50% 本题对学生的阅读理解能力要求较高,属于无图考图问题,需要根据题意画出图形,分析和整理已知信息,设计求解思路. 例7(北京卷第21题)定义RP数列{an}:对于实数p,满足: ①a1+p≥0,a2+p=0; ②∀n∈N+,a4n-1 ③am+n∈{am+an+p,am+an+p+1}. (Ⅰ)对前4项2,-2,0,1的数列,可以是R2数列吗?说明理由; (Ⅱ)若{an}是R0数列,求a5的值; (Ⅲ)是否存在p,使得存在RP数列{an},对∀n∈N+,满足Sn≥S10?若存在,求出所有这样的p;若不存在,说明理由. 分析:首先需要考生对题目中给出的符号语言能够读懂、读全、理解,然后需要对符号语言提供的多个信息进行梳理、整合、挖掘、转化,找出这些信息“背后”隐藏的结论;最后运用批判性思维进行逻辑推理,再用符号语言书写表达. ①提供的信息是:a1≥-p,a2=-p; ②提供的信息是:a4>a3,a8>a7,a12>a11,…,a4n>a4n-1; ③提供的信息是:am+n=am+an+p或am+n=am+an+p+1. 若令m=1,则可以得到an+1=a1+an+p或an+1=a1+an+p+1. ④ 于是可以得到an+1≥an. ⑤ 若再令n=1,则可以得到a2=2a1+p或a2=2a1+p+1. ⑥ 由①和⑥可得a1=a2=-p. ⑦ 于是由信息⑦知(Ⅰ)中给出的数列不是R2数列. (也可以直接验证:由信息③知a2=2a1+p=6或a2=2a1+p+1=7与a2=-2矛盾,故(Ⅰ)中给出的数列不是R2数列) 在(Ⅱ)中,由于p=0,由信息①②③④⑤⑥⑦不难推出数列{an}为 0,0,0,1,1,1,1,2,2,2,2,3,……, 所以a5的值为1. 在(Ⅲ)中,由前面提供的七条信息,不难得到RP数列{an}为 -p,-p,-p,-p+1,-p+1,-p+1,-p+1, -p+2,-p+2,-p+2,-p+2,-p+3, -p+3, -p+3,-p+3, …, 进一步思考:若把条件改为“对∀n∈N+满足Sn≥S8(或S9)”,同样得到p=2;若把条件改为“对∀n∈N+满足Sn≥S11”,则可以得到p∈[2,3]等. 对信息整理能力的考查往往还体现在一个题目的前一问的解答信息对后面问题解答的提示与借用上.比如本题在解答第(Ⅱ)问时,要使用第(Ⅰ)问的解答信息;在解答第(Ⅲ)问时,需要借助第(Ⅰ)问的信息,更需要借助第(Ⅱ)问所获得的数列提供的规律性信息. 在高考数学中,对阅读理解能力的考查,主要体现在对文字语言、符号语言、图形语言的阅读理解能力考查上.“数学思维是以数和形为思维对象,以数学语言和符号为载体,以认识和发现数学规律为目的,所以抽象的符号语言是数学的重要特征,更是思维操作的便捷材料.对符号的理解、掌握是数学解题的关键.”[7] “必备知识是指即将进入高等学校的学习者在面对与学科相关的生活实践或学习探索问题情境时,高质量地认识问题、分析问题、解决问题所必须具备的知识.”[8]它是由数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”)构成的基本知识体系[9],这一知识体系由陈述性知识和程序性知识构成,是应对情境所必须具备的各种复杂的产生式系统.必备知识与关键能力一样,是学科素养的基础.从2021年的数学试卷中能够看到考查必备知识有以下特征. 在2021年高考数学的十套试卷中,每套试卷都包含了一定比例的基础性试题,引导学生打牢知识基础. 分析:由倍角公式及已知,得 只要学生的基础扎实,解决此题并不困难. 加强试题的综合性是高考考查能力的重要举措,这种综合可以是同一知识板块中的多点综合,也可以是跨板块间的多点综合,还可以是多知识点与思想方法的综合等等,这种纵横交错的综合要求学生能够触类旁通、融会贯通. A.当λ=1时,△AB1P的周长为定值 B.当μ=1时,三棱锥P-A1BC的体积为定值 分析: 如图,易知点P在矩形BCC1B1内部(含边界). 对于A,当λ=1时,此时P在线段CC1上,△AB1P周长不是定值,故A错误; 对于B,当μ=1时,此时P点轨迹为线段B1C1,而B1C1∥BC,B1C1∥平面A1BC,则有点P到平面A1BC的距离为定值,所以其体积为定值,故B正确. 本题的综合性很强,需要学生能够熟练运用数学知识与方法,灵活多样地分析问题和解决问题,对能力提出了较高要求. 试题重视对数学本质的考查,突出对理性思维、数学探究能力的考查. 本题对函数奇偶性定义、函数周期的定义、分段函数等概念的本质进行了深入考查,需要学生能熟练运用概念、原理灵活思考和探究问题. 2021年的试题还加强了对运用所学知识分析和解决实际问题能力的考查,主要体现在学生要能够善于观察现象,学以致用,具备较强的理论联系实际能力和实践能力. 例11(北京卷第8题)对24小时内降水在平地上的积水厚度(mm)进行如下定义 0~1010~2525~5050~100小雨中雨大雨暴雨 小明用一个圆锥形容器接了24小时的雨水,则这一天的雨水属于哪个等级( ). A.小雨 B.中雨 C.大雨 D.暴雨 本题以学生综合实践活动为背景,通过自制雨量器,收集雨水,测量降雨量.题目源自古代降雨量测量的真问题,旨在考查学生数学应用能力,弘扬传统文化. 2021年高考数学许多试题能够合理设置问题情境和设问方式,促使学生主动思考,善于发现新问题,找到新方法、新规律,得到新结论等,从而有效的考查学生独立思考、发散思维、逆向思维、敏锐地发掘和捕捉、大胆猜测与周密论证等与创新密切相关的能力与素养. 例12(浙江卷第22题)设a,b为实数,且a>1,函数f(x)=ax-bx+e2(x∈R) (Ⅰ)求函数f(x)的单调区间; (Ⅱ)若对任意b>2e2,函数f(x)有两个不同的零点,求a的取值范围; 于是,当lna>2e2,即a>e2e2时,易知g(b)在(2e2,lna)单调递增,在(lna,+∞)单调递减,此时,可得g(lna)>0,因此不满足恒成立;当lna≤2e2,即1 综上可得,满足题意的a的取值范围是(1,e2]. (Ⅲ)f(x)=ex-bx+e2,运用导数不难得到当x=lnb>4时,f(x)min=f(lnb)=b-blnb+e2 本题的第(Ⅰ)、(Ⅱ)问均属于常规问题,需要学生基础扎实,融会贯通;第(Ⅲ)问需要学生能够敏锐地发现并捕捉隐含信息,通过变形转化进行猜想推测,再运用逻辑推理进行周密论证,考查学生大胆尝试探索新方法、解决新问题的创新思维意识和思维能力. 总之,在深化高考综合改革的当下,2021年的高考数学试卷很好地诠释了《中国高考评价体系》的“一核”、“四层”、“四翼”的考查理念.分析和研究这些试题,能够使我们深入理解高考的核心功能,准确把握高考的考查内容和考查要求,对全面贯彻教育方针,落实立德树人根本任务,发展素质教育,推进数学新课程改革都具有重要的引领作用.1.4 结合数学学科特点,落实“五育并举”方针
2 以学科素养为导向
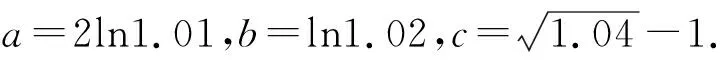

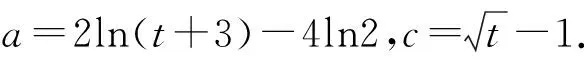
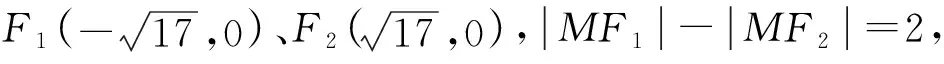





3 以关键能力为重点


4 以必备知识为基础
4.1 强调基础扎实




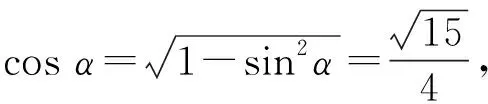
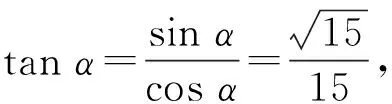
4.2 强调融会贯通
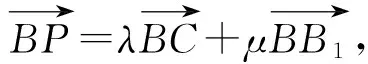





4.3 强调数学本质


4.4 强调学以致用



4.5 强调创新意识和创新思维