一道概率问题的多层次探究①
朱胜强
(南京外国语学校 210008)
1 问题的生成
概率教学时曾遇如下问题:
题1汽车站每天均有三辆开往N市分为上、中、下等级的客车.某人在车站准备乘车前往N市,但不知道客车的具体情况,也不知道发车顺序.为了尽可能乘到上等车,他采取如下策略:先放过第一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.那么他乘到上等车的概率是多少?
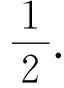

表1
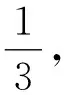
题2n个互不相等的数随机排成一列,某人事先不知各数大小,顺次逐个观察,并从中选取一个数,不得回头选取.为使取得的数最大,他采用如下策略:
先观察前k个数,确定它们的最大值,再观察其余的n-k个数.一旦发现比前k个数中最大值大的数,即选取该数,否则选取最后一个数.
问:k取多少时取得最大数的概率最大?最大概率是多少?
2 多层次的探究
2.1 设计随机试验 探求基本结论
学生容易想到的方法是从概率的定义入手.教材对于随机事件的概率有如下定义:
一般地,对于给定的随机事件A,在相同条件下,随着试验次数的增加,事件A发生的频率会在某个常数附近摆动并趋于稳定,我们可以用这个常数来刻画事件A发生的可能性大小,并把这个常数称为事件A的概率.
不妨将问题2中所说的“取得最大数”记为事件A,当k确定后,随机事件A便是给定的.下面用GeoGebra模拟随机试验,并对所得数据进行统计分析以探寻事件A发生的概率与k之间的联系.为研究方便,取n=100,并将100个数记为1,2,3,…,100,它们的一个随机排列用数列a1,a2,a3,…,a100表示.
取定正整数k(1≤k≤99),可得两个序列l1:a1,a2,…,ak与l2:ak+1,ak+2,…,a100.
求出序列l1中元素的最大值,记为M.
将序列l2中的元素依次与M比较大小,并将ak+1,ak+2,…,a99中第一个大于M的元素记为a,若不存在这样的a,则将a100记为a.若a=100,则事件A发生.
对于给定的k值,数1,2,3,…,100的任一随机排列都对应着一次随机试验,一定量的随机试验可确定事件A发生的频率.改变k的取值,相应的频率便会发生变化,据此可估计出k取何值时,事件A发生的概率最大.
上述随机试验中的许多环节都可借助GeoGebra的固有操作功能来完成.如:
随机排列(<列表>),可以给出<列表>中所有元素的一个随机排列.
提取(<列表>,<起始位置>,<终止位置>),可以生成数列中任意两项间所有项构成的子数列.
最大值(<数字列表>),可以求出一个数列中的最大项.
条件子列(<条件>,<变量>,<列表>)可以找出数列中满足一定条件的所有项.
如果(<条件>,<结果>,<否则>)可以根据给定条件,生成相应的结果.
在进行随机试验时,为节省时间,还可采用批量实验操作.对确定的k值,一次性给出100个甚至更多的随机排列的数列.
表2是针对每个k值分别进行了200次随机试验获得的频率值.可以看出,当k很小或很大时,对应的频率值都比较小.当k的值在20~60间时,频率值相对较大.k与频率之间的关系是否可以用数学模型作更精细的描述呢?
依据表2,以k为横坐标,对应的频率为纵坐标画出散点图(如图1).这些点似乎在一条曲线附近摆动,不妨选用多项式来拟合.
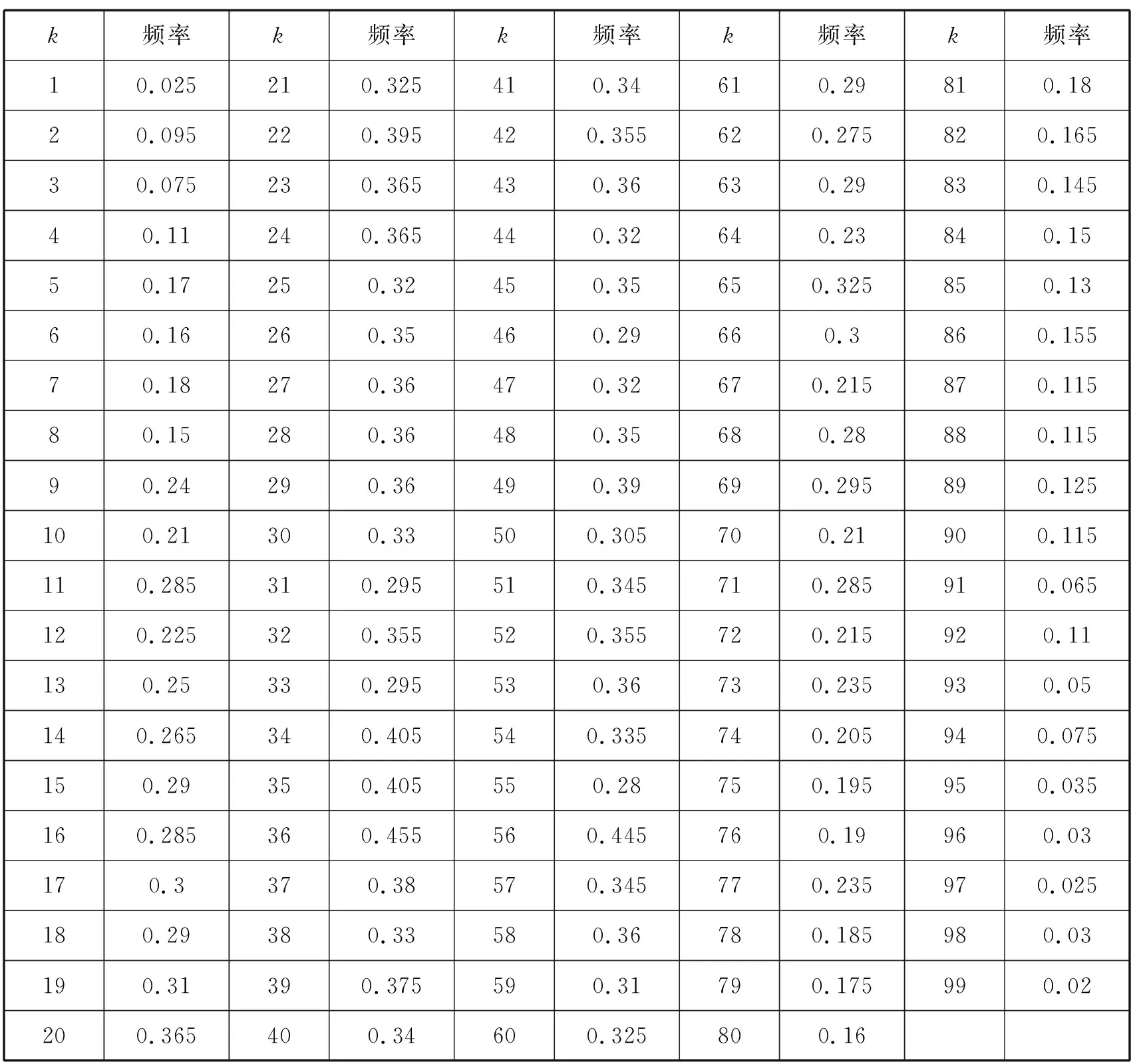
表2

图1
分别用2次,3次,4次,5次,6次多项式拟合.并计算相应的误差平方和(如表3).

表3
可以看出,次数为2时的误差平方和明显较大.注意到不同次数曲线在自然平滑方面的差异,可选择4次多项式作为拟合函数.此时多项式函数为:
f(x)=10-10(158x4+44876x3-5299992x2+236862449x+291392669).
由f(x)可求得其图象上纵坐标最大的点为(36.1,0.378).这说明,当k=36时,频率有最大值0.378.
上述各项操作也都可在GeoGebra中直接完成.如:
多项式拟合(<点列>,<多项式次数>)可以生成指定次数的多项式,并显示出多项式函数的图象.
误差平方和(<点列>,<函数>)可以得到回归模型的误差平方和数值.
最大值(<函数>,
试验结论表明,当k取36时,事件A发生的概率最大,最大值为0.378.
当然,这只是进行200次随机试验获得的结论.如果将试验的次数增大,有可能得到更为精确的结论.
2.2 依据计数原理 探索一般规律
试验获得的结果只是一种近似值.是否能得到k与A的概率间的一般规律呢?
由于随机事件A与n个数的随机排列相对应,每一个排列又是等可能的.因此可以考虑用古典概型来解释.
n个不同的数排成一排,即为n个元素的全排列,共有n!个等可能的基本事件.下面考察事件A包含的基本事件数.
“取得最大数”可以分为在k+1位,第k+2位,…,第n位取得最大数.
若在第i(k+1≤i≤n)个位置取得最大数,则n数进行排列时需满足如下条件:
(1)第i个位置排n个数中的最大数;
(2)前i-1个位置上的最大数排在前k位.
满足上述要求的排列个数可按如下方法求得:
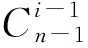
第二步,将上一步中选出的i-1个数中最大数排在前k项中的某一项,有k种方法;
第三步,将上一步中剩下的i-2个数在前i-1项中余下的i-2个空位上作全排列,有(i-2)!种方法;
第四步,将剩下的n-i个数在第i+1到第n个位置上作全排列,有(n-i)!种方法.
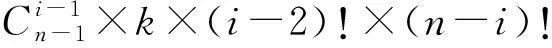
所以,事件A包含的基本事件数为
由古典概型概率计算公式可知
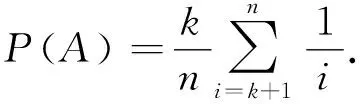
若n=100,k=36,
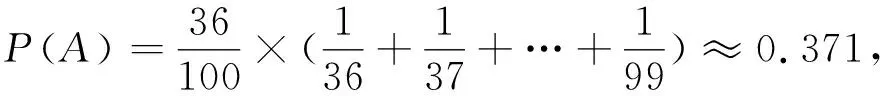
前面得到的数据与此还是比较接近的.
是不是k=36时对应的P(A)最大呢?
仍回到一般情形.
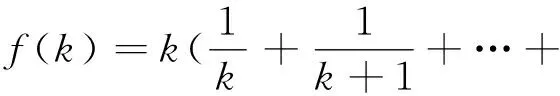
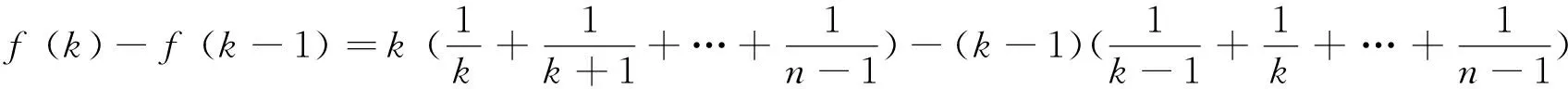

有f(k)>f(k-1),此时数列{f(k)}单调递增;
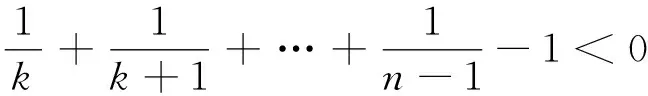
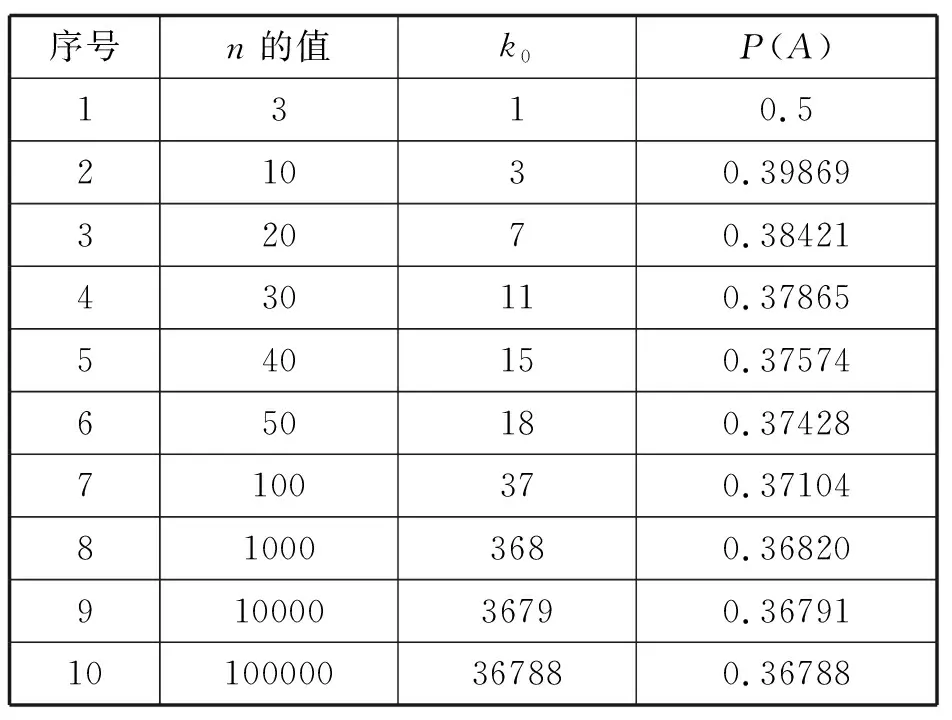
有f(k) 则g(k)随着k的增大而减小. 若n≥3,则必有g(1)>1,g(n-1)<1. 因此,存在最大正整数k0使g(k0)≥1成立.此时有 f(1) 所以,f(k0)是f(k)的最大值. 因此,对于确定的n(n≥3),满足条件 的最大k值(记为k0),可使P(A)取得最大值. 对于给定的n,借助电脑不难求得这样的k0及对应的P(A)(如表4). 表4 从表中可以看出,当n= 3时,k0取1,此时P(A)取值0.5,这与上文计算结果吻合.当n=100时,k0取37,这与试验结果略有偏差. 根据g(k)的单调性,要找到使 成立的最大的正整数k0, 图2 在新课程标准中,数学探究被赋予了“提升学生学科能力和素养”的重要使命.“问题”是探究的载体,是活动组织与设计的核心.本文中的问题源于教学,是学生感兴趣的问题,是教学活动中自然生成的问题.这样的问题用于探究活动,有利于调动学生的积极性与参与度,提升活动效果.因此,教师在教学中要有问题意识,注意发掘与积累生成性的问题资源. 有许多探究活动仅局限于章节范围内的知识,一旦获得结论,活动便告结束.本文给出的探究问题,在对数学能力的要求上富有层次性,处于不同学习阶段或不同水平层次上的学生都可展开相应的研究.随着数学能力的不断提升,持续探究所获得的认识也会不断深化.在“刷题”盛行,追求“快思”的今天,这样的探究对于培养学生会用“数学的思维思考世界”显得尤为可贵. 信息化手段在探究过程中发挥了不可或缺的作用.如果没有信息技术的帮助,大量重复的随机试验几乎无法进行,对收集得到的数据的分析也将困难重重,探究中一些猜想的验证也无法实施.所以,有效开展探究活动,不可忽视信息技术因素的作用,教师需要不断了解因信息技术进步而引发的教学中的改变.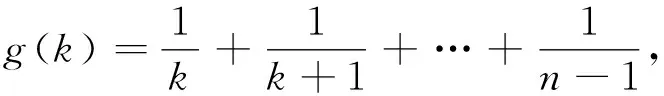
2.3 运用极限思想揭示问题本质


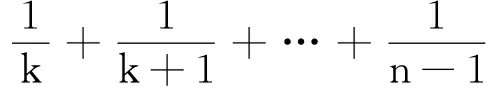

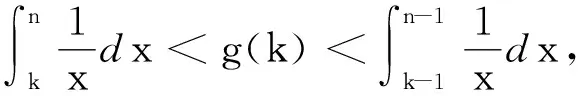

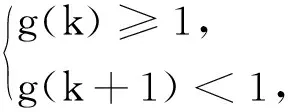



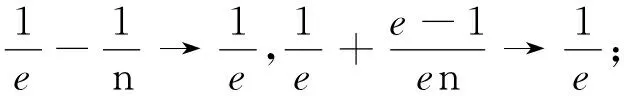
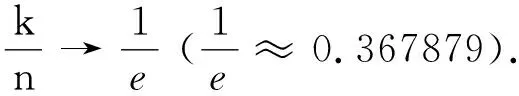
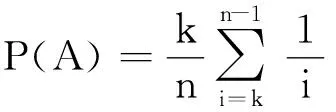

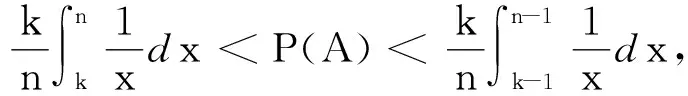

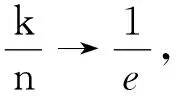
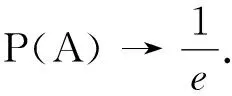

3 实践后的思考

