由独立重复实验浅谈高中数学建模

马晓娟

摘 要：独立重复实验是研究随机现象的重要途径之一，很多概率模型的建立都以独立重复实验为背景。数学模型是数学与实际现象之间的桥梁，数学核心素养包括数学建模、数据分析等素养。本文以“独立重复实验与二项分布”教学为例，探讨了如何开展高中数学建模活动。

关键词：高中数学;数学建模;独立重复实验

中图分类号：G427                       文献标识码：A                    文章编号：2095-624X（2021）30-0059-02

引 言

近年来，数学模型和数学建模这两个术语使用的频率越来越高，人们对数学建模的关注程度也与日俱增。数学的应用不仅在它的传统领域——物理领域继续取得重要进展，还迅速进入人们生产和生活的许多新领域，如经济、人口、生态、医学、社会等领域。人们乐于在外出时乘坐舒适、快捷又安全的大型客机，其整个设计过程是由一种将数学与计算机相结合的被称为计算机辅助设计（CAD）的先进的数学技术完成的。其生产过程则是用工程师建立的控制生产过程的数学模型，对控制装置做出相应的设计和计算后实现的。为了保障人民的生命健康，医学专家经常开发和研制新的药物和医疗器械，而一种新药或器械的试制必须经过反复实验，以获得充足的数据，并利用数学方法模拟疗效数学模型后方可分析疗效，从而有效地指导临床治疗[1]。

高中数学新教材和旧教材相比，更注重数学的应用和对数学核心素养的培养，注重应用数学知识构建模型，从而培养学生的数学建模能力。

一、内容分析

独立重复实验与二项分布是用事件的独立性来研究一类问题，概率论中被称为伯努利概型，伯努利概型是概率论中研究较多的数学模型之一，概括了许多实际问题，因而很有实用价值。它也为今后进一步学习概率论奠定了基础。值得一提的是，我们由伯努利概型可以解决一类“随机游动”的问题。下面，笔者将结合教材中的例题，以及醉汉随机游走和姚明投球命中率的实例，按照数学建模的五个步骤，建立二项分布模型，发展学生的数学建模和数据分析素养。这也是这节课的重点，即理解独立重复试验、二项分布，并应用二项分布模型解决一些简单的实际问题。学生可采用自主探究、合作交流的形式，从具体事例中归纳出数学概念，充分体会知识的发现过程，进而发展自身的数学抽象素养;利用二项分布的有关知识解释生活中的现象，用数学的语言表达世界，发展数学建模和数据分析的核心素养[2]。

二、学生情况分析

学生已有的认知基础：通过前面的学习，学生已经初步掌握了有关概率和统计的基础知识，如可能事件概率、互斥事件概率、条件概率、相互独立事件概率的求法、随机变量分布及简单的组合知识。另外，学生也学习过一些研究问题的方法，如特殊到一般、具体到抽象等，且有了一定的抽象概括能力。这为学生学习本节内容做好了知识和方法上的铺垫。

可能遇到的困难：本节内容是从生活实例出发，引导学生归纳出抽象n重伯努利实验的概型，并利用伯努利概型的有关知识解释生活中的一些现象。这对学生抽象概括能力和应用数学语言的表达能力要求较高。利用一个新的概率模型解释生活中的现象对学生来说有一定的困难。教学难点：利用二項分布模型来解决实际问题，即伯努利模型的构建。

三、教学过程设计

（一）分析实例

实例1：随机游走模型

想象在曼哈顿东西南北格点化的街道中有一个醉汉，他每次到达一个交叉路口时都会随机选择向东、向北两个方向中的一个，然后继续前行;在走到下一个路口时又随机选择一个方向……如此继续下去，这个醉汉回到家的概率是多少？

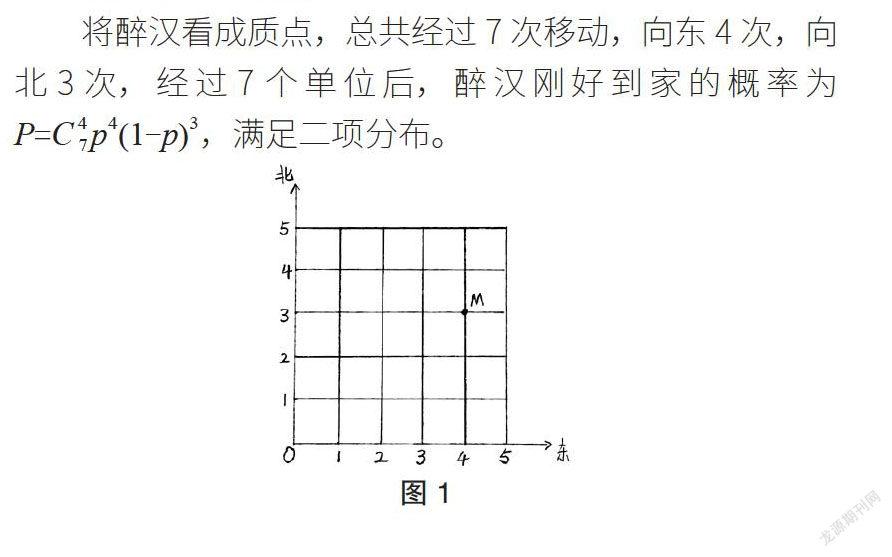
模型假设：醉汉每个时间单位到达一个交叉路口，向东或者向北前进，向东的概率为p，向北的概率为1-p，假设醉汉的家在点M（4，3）处（见图1），求经过7个时间单位后醉汉刚好到家的概率。

模型建立与求解：

将醉汉看成质点，总共经过7次移动，向东4次，向北3次，经过7个单位后，醉汉刚好到家的概率为P=C47p4（1-p）3，满足二项分布。

实例2：姚明投球

姚明作为中锋，他职业生涯的罚球命中率为0.8，假设他每次投篮的命中率相同，请问他4投3中的概率是多少？（以上有关数据由学生课前查阅资料并收集整理）

模型假设：假设姚明每次投篮的命中率是相同的。

模型建立与求解：

问题：姚明作为中锋，他职业生涯的罚球命中率为0.8，假设他每次投篮的命中率相同，请问他4投3中的概率是多少？设姚明投中球的个数为x，x的分布列是怎样的？

学生活动：小组合作讨论。

分解问题：（1）在4次投篮中他恰好命中3次的情况有几种？（2）说出每种情况的概率是多少？（3）上述四种情况能否同时发生？（4）设姚明投中球的个数为x，x的分布列是怎样的？

教师行为：引导学生观察分析，让学生大胆去说，教师逐步修正，完善学生的说法，培养学生分析问题和解决问题的能力。

答案（学生拿自己的草稿在投影下讲）：

Ai表示姚明第i次投中球，则表示姚明第i次没投中球。姚明4投3中包含以下事件：，，

，共种，每种事件的概率为。故4投3中的概率为。x的分布列为（见表1）。

上述解答是一个对前面所学知识的应用过程。学生看到最后的结果，有一种“拨开云雾见青天”的感觉，这不就是二项式定理吗？学生热情高涨，把对知识的学习和掌握过程变成了对知识的探索、发现、总结、创新的过程。