一类加权Kirchhoff方程非线性Liouville定理

曹悦璠，方钟波

(中国海洋大学数学科学学院，山东青岛266100)

1.引言

本文中，我们考虑一类具有加权函数的Kirchhoff方程

其中N≥1，a，b∈R，加权函数ω1和ω2均为满足适当条件的正函数且可能为Hardy势函数，非线性项f为非负函数且可取为Gelfand(或Liouville)项eu.一般地，具有Hardy势函数的椭圆方程(1.1)的解可能具有奇性，故很自然需要在一个适当的加权Sobolev空间中研究(1.1)的弱解.类似于文[1]，对我们定义

众所周知，方程(1.1)可理解为粘弹性振动理论中Kirchhoff型波动方程及达朗贝尔波动方程的稳态问题.从数学角度来说，方程(1.1)不是逐点恒等式，因此方程(1.1)是非局部问题且与局部问题相比有着较大的难度.迄今为止，许多学者致力于椭圆型方程稳定解的存在性与非存在性及正则性的研究并取得了许多进展.我们注意到，在这些进展中人们对有限Morse指数解或者在紧集外稳定解感兴趣.大部分学者对这些解的Liouville型定理感兴趣的原因在于有界区域中稳定解的非存在性与对应方程稳定解的先验估计有十分紧密的联系.其中，关于局部方程-Δu=f(u)的研究方面见专著[2]及相关文献;关于具有加权函数的局部方程研究方面，我们参考了文[3-7].比如，Cowan和Fazly[7]研究了加权半线性椭圆方程Liouville型定理

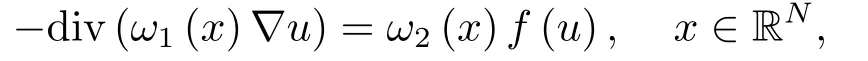
其中非线性项f(u)=eu，up(p＞1)，-u－p(p＞0).他们得到了稳定上解和下解的存在性与非存在性结论且其依赖于维数、指数以及权函数在无穷远处的行为.在有些结论中，给ω1适当的单调性假设，也能得到相同的结果.此外，具有加权指数源项的p-Laplacian方程柯西问题稳定解的Liouville定理的研究方面，我们重点参考了文[1].

本文中，我们的目的在于建立具有加权函数的Kirchhoff方程新的Liouville型定理.实际上，Lions在文[8]中首次在泛函分析框架下研究Kirchhoff模型，之后，Kirchhoff型方程受到了广泛的关注且已有很好的成果，读者可以参看关于Kirchhoff问题可解性的文[9-13](具有乘幂型源项)及文[14-16](具有指数型源项).最近，Le等[16]考虑了Hardy-Henon型Kirchhoff方程

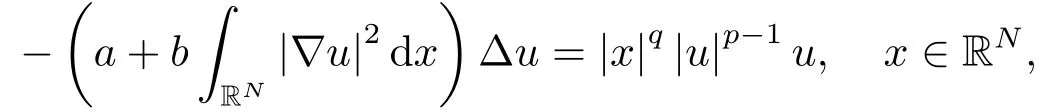
其中常数a，b≥0，a+b＞0.他们在适当的条件下证明了方程不存在非平凡稳定解的结论.Huynh等[17]考虑如下Henon型的Kirchhoff方程:

其中a∈R，b∈R{0}.他们利用试验函数法得到了在适当的条件下问题弱解的非存在性及具有指数型源项问题稳定解的非存在性.

综上所述，具有加权函数的Kirchhoff方程(1.1)弱解与稳定解的非存在性(Liouville型定理)研究还未十分完整.其主要难点在于找到空间的维数、加权函数在无穷远处的行为或单调性、非线性项f(u)及Kirchhoff算子对问题解的非存在性的影响.由此启发，我们利用构造试验函数技巧，建立方程(1.1)新的Liouville定理.

本文的剩余部分结构如下:在第2节中，我们引入一些记号，方程(1.1)弱解和稳定解的定义及引理.第3，4节中，我们陈述主要结论，并利用构造试验函数的技巧，证明方程(1.1)弱解的非存在性及具有指数型源项的方程(1.1)稳定解的非存在性.

2.准备知识及主要结论

本节中，我们给出一些记号，问题(1.1)弱解与稳定解的定义、引理并陈述主要结论.

为了描述简便，我们用C表示一般的常数且每行的常数C可能表示不同的常数;同时，当某个常数依赖于ε时用Cε表示.BR表示以0∈RN为中心半径为R的球.空间X的定义如下:若若.

由Hardy势导致椭圆方程(1.1)解可能具有奇性，故一般考虑弱解.下面，我们给出问题(1.1)弱解及稳定解的定义.

定义2.1若函数u∈X满足且对有

则称函数u是方程(1.1)的弱解.

定义2.2若(1.1)的弱解u满足：对有

则称u是方程(1.1)的稳定解.

注2.1由前述的定义知，函数u是方程(1.1)的弱解意味着u是能量泛函E(u)的临界点，而稳定解则表明能量泛函E(u)在u处的第二变分是非负的，即，对有E′′(u)[φ，φ]≥0.这里，问题(1.1)对应的能量泛函为

则我们有

于是

因此I′(0)=0等价于

即E(u)的临界点u是问题(1.1)的弱解.

其次，我们求I′′(0).

故有

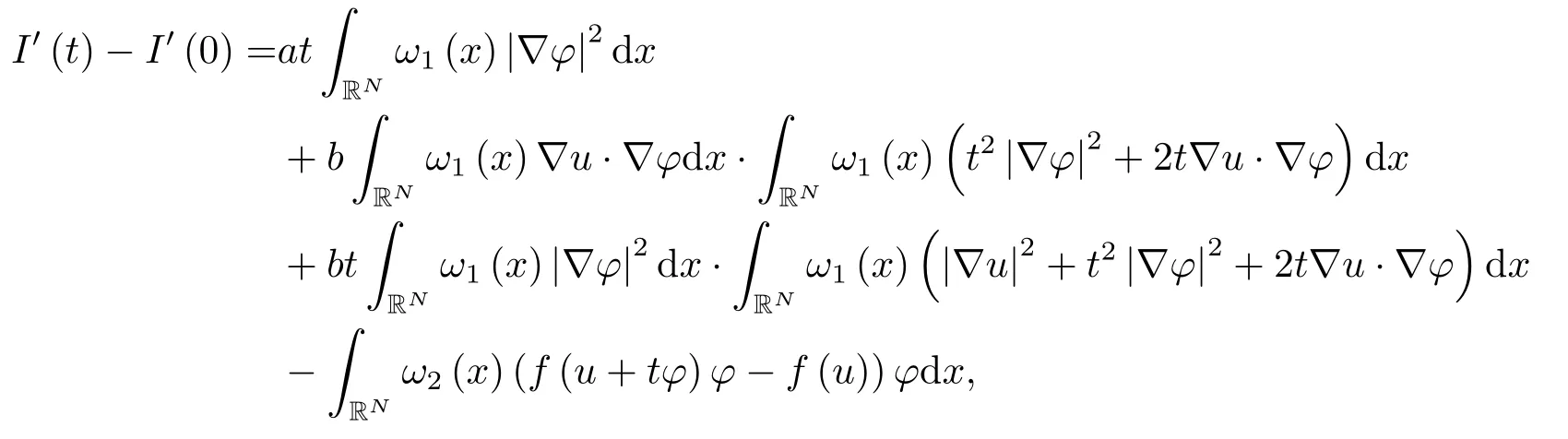
且

因此，我们易知I′′(0)≥0等价于

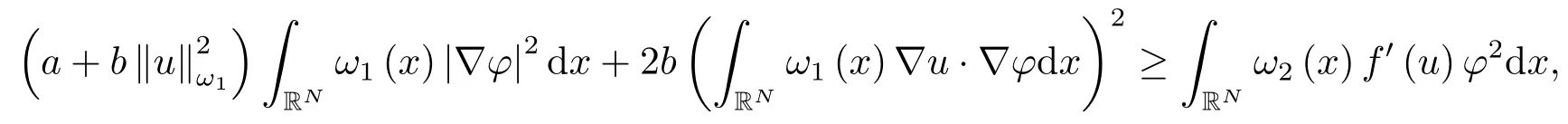
即E(u)的极小值点u是问题(1.1)的稳定解.

紧接着，我们导出主要定理的证明所需的引理.

引理2.1若u是方程(1.1)的稳定解，则对有

证利用加权的Hlder不等式，我们有

由稳定解定义(2.2)及(2.4)，我们得到

引理2.1证毕.

注2.2由稠密性理论知，对前述的(2.1)，(2.2)及(2.3)式同样成立.

注2.3如果ab≥0且a+b＞0，势函数ω1(x)保证可积，非线性函数f是严格单调递增的且u是方程(1.1)的稳定解，则事实上，我们取试验函数满足:0≤φ≤1，且

其中常数C不依赖于R.

将φ代入到(2.3)中，并利用的φ性质，我们导出

在上式中，两边取极限R→∞，即可得

RN ω2(x)f′(u)dx=0.

现在，我们详细陈述本文的主要结论.

定理2.1假设a∈R，b0，非线性函数f为一个非负函数.若对于a.e.x∈RNBR0，有0≤ω1(x)≤A|x|p且ω2(x)≥B|x|q，其中A，B及R0为正常数，则方程(1.1)满足

的弱解u∈X不存在.

推论2.1在定理2.1的条件下，则满足下列条件之一的方程(1.1)不存在弱解:

1)p＜1，N≤1-p;

2)infRf＞0，q∈(-∞，-N]

推论2.2定理2.1的条件成立且若f非减(或非增)，则方程(1.1)不存在有下界(或上界)的弱解.

对非线性项f(u)为指数函数情形，我们得到了如下稳定解的非存在性结论.为了描述方便，我们简记如下表达式:

定理2.2假设ab≥0且a+b＞0，f(u)=eu.如果存在当R→∞时满足J→0且K→0，则方程(1.1)不存在稳定解.

推论2.3假设ab≥0且a+b＞0，对于a.e.x∈RNBR0有0≤ω1(x)≤A|x|p，ω2(x)≥B|x|q，其中A，B及R0为正常数，若则方程(1.1)不存在稳定解.

注2.4由定理2.2的证明过程易知，对ω1给定适当的单调性假设也可得到方程(1.1)稳定解不存在性结论.

定理2.3假设ab≥0且a+b＞0，f(u)=eu.且对充分大的|x|，ω1(x)满足∇ω1(x)·x≤0，如果存在当R→∞时满足J→0，则方程(1.1)不存在稳定解.

推论2.4假设ab≥0且a+b＞0，f(u)=eu，ω2∈L∞，若对充分大的|x|有

推论2.5若在推论2.4中势函数ω1的条件换成:对充分大的|x|有

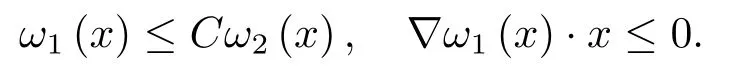
3.弱解的非存在性

对∀R＞R0，我们介绍满足0≤φ≤1，且

其中常数C不依赖于R.

定理2.1的证明假设方程(1.1)存在满足(2.5)式的弱解u∈X.选取试验函数φ，我们有

结合(3.1)及(3.2)，我们导出

再由条件(2.5)知，存在R′∈N，R′＞R0使得当R＞R′时满足

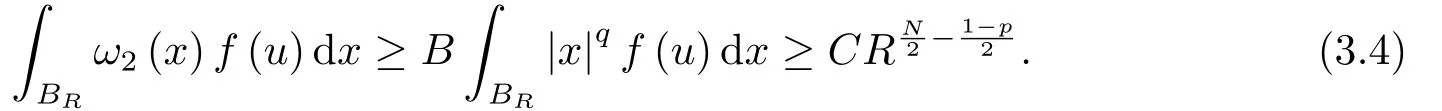
结合(3.3)及(3.4)易知，当R＞R′时，我们有

其中C不依赖于R.

取R=R′，R′+1，R′+2，···且对(3.5)式左右两边关于R求和，我们得到

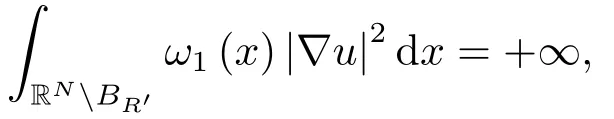
推论2.1的证明利用反证技巧.假设方程(1.1)存在弱解u.显然，当p＜1，N≤1-p时，弱解u满足(2.5)式.与定理2.1的结论矛盾.

又有

且若q∈(-∞，-N]，则积分发散.因此，由(3.6)知(2.5)式成立且与定理2.1矛盾.

且将上式代入(3.6)中，我们得到

对(3.7)式两边取R→∞极限，易知(2.5)式成立且与定理2.1的结论导致矛盾.推论2.1证毕.

推论2.2的证明利用反证法.若f非减且方程(1.1)存在有下界的弱解u.记u的下界为u1，则infRf=f(u1)且与推论2.1导致矛盾.关于f为非增情形类似，故此处省略.推论2.2证毕.

4.稳定解的非存在性

由u∈X易知，u不一定是局部有界.因此，我们不能取φ=eαuψ为试验函数.类似于文[1，17]，我们利用截断技巧来克服这个困难.对每个k∈N定义如下正函数ak(t)和bk(t)∈C1(R):

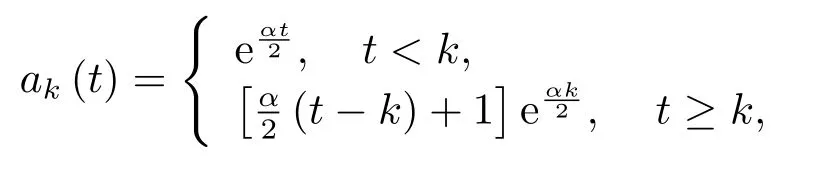
及

其中α＞0为待定常数.同时，直接通过计算得到，对∀t∈R，我们有

其中C仅依赖于α.此外，由知

定理2.2的证明利用反证技巧.假设方程(1.1)存在稳定解u.

现在，基于ak(u)，bk(u)的定义，我们的证明将分为四个步骤展开.

步1对任意的ε∈(0，1)任意的k∈N，及任意的非负函数存在一个常数Cε＞0使得

为了证明(4.2)，根据弱解定义，我们取试验函数为φ=bk(u)ψ2代入(2.1)中并利用带ε的Young不等式，我们导出

且整理后，我们得到

步2对任意的k∈N，及任意的非负函数有

为了证明(4.3)，我们取试验函数φ=ak(u)ψ.直接计算，我们有

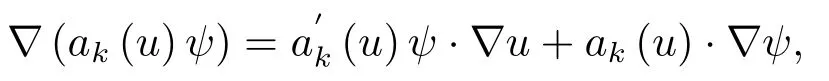
且根据稳定解定义，及引理2.1，我们导出

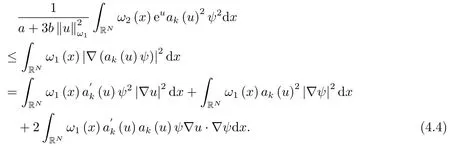
对(4.4)最后一项，通过分部积分直接计算得到

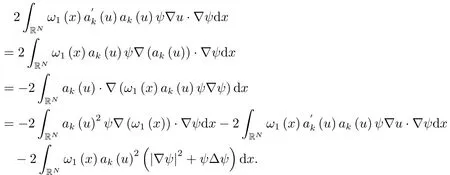
整理后，我们有

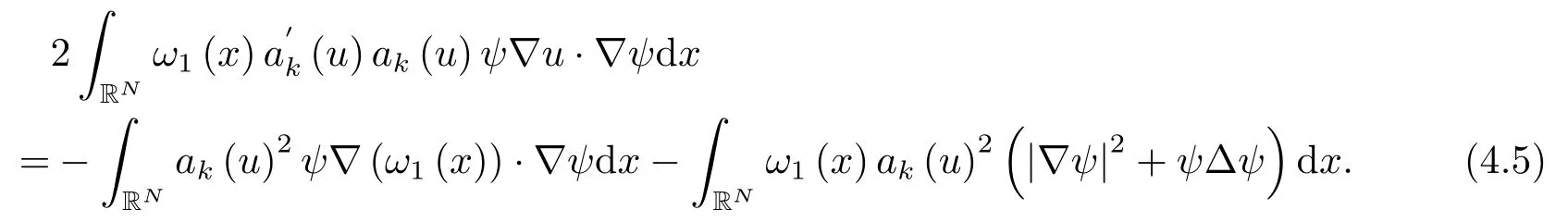
将(4.5)代入(4.4)，我们得到

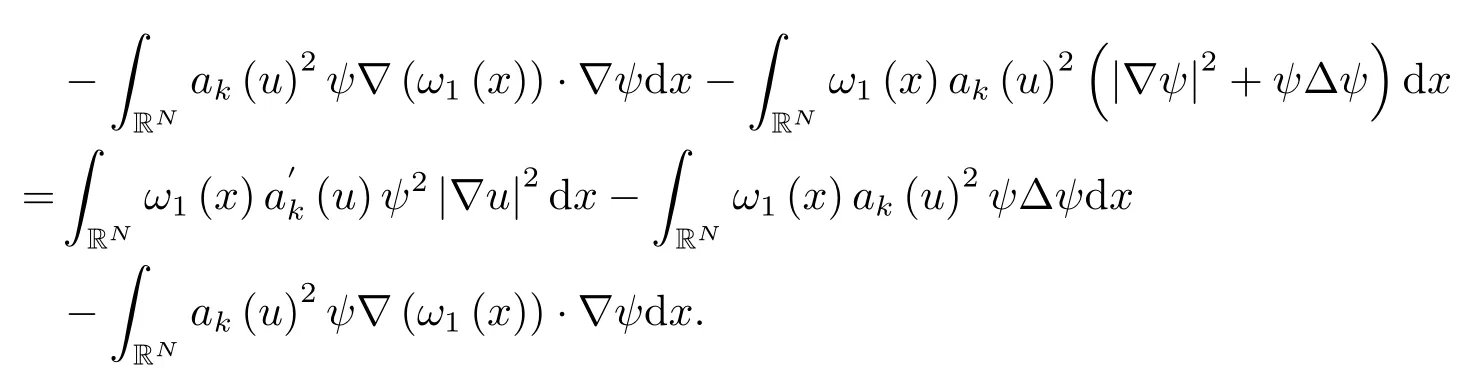
步3存在常数C=C(α)＞0使得对任意非负函数我们有

为了证明(4.6)，结合(4.2)，(4.3)，并利用(4.1)，我们可导出

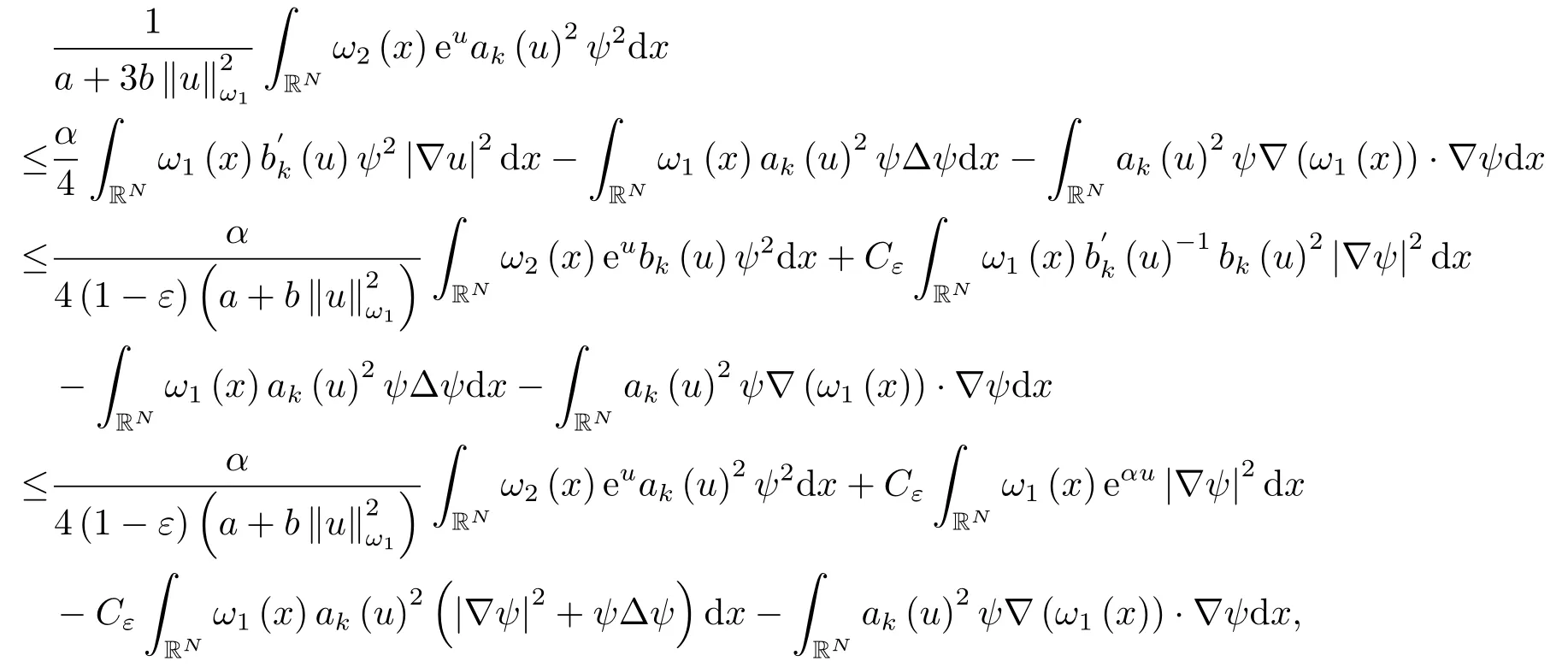
并整理后，我们有

其中常数C仅依赖于α.

在(4.8)式中取k→∞极限并利用单调收敛定理，我们得到

步4当R→∞时，J→0，K→0，则方程(1.1)不存在稳定解.

为了证明上述结论，我们令R＞0且取ψ=ξm，其中m＞0待定，满足0≤ξ≤1，且

其中常数C不依赖于R.

再由(4.6)式，我们有

其中常数C1，C2＞0仅依赖于α，m.

及

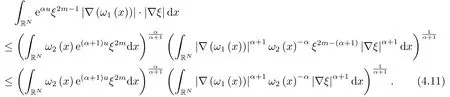
将(4.10)及(4.11)代入(4.9)中，再由ξ的性质，我们导出

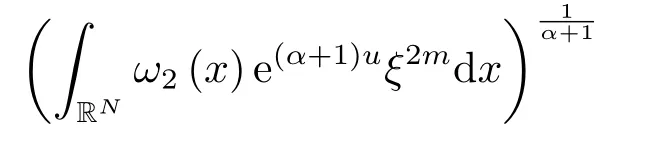
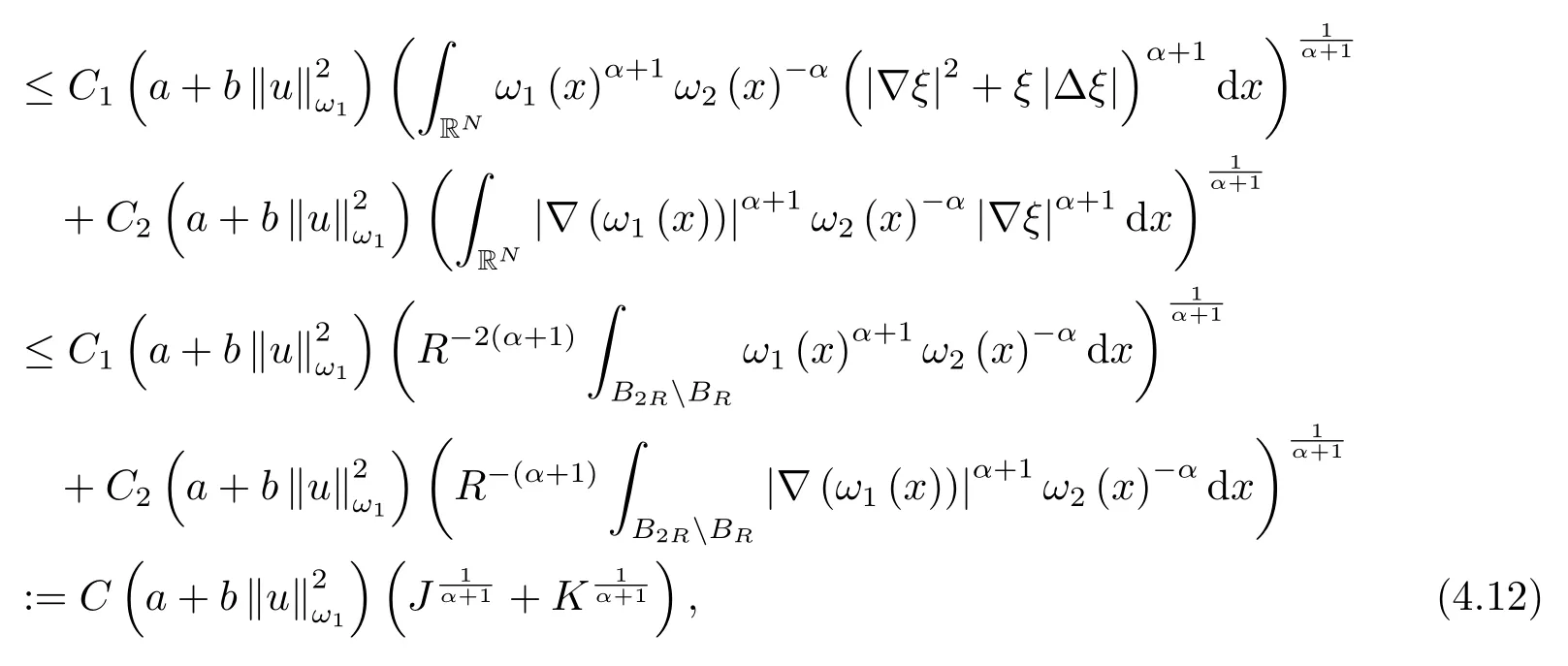
且有

对(4.13)式两边取R→∞极限并由条件:当R→∞时，J，K→0易知

且导致矛盾.定理2.2证毕.

推论2.3的证明根据ω1(x)，ω2(x)的假设，我们取∀R＞R0，有

和

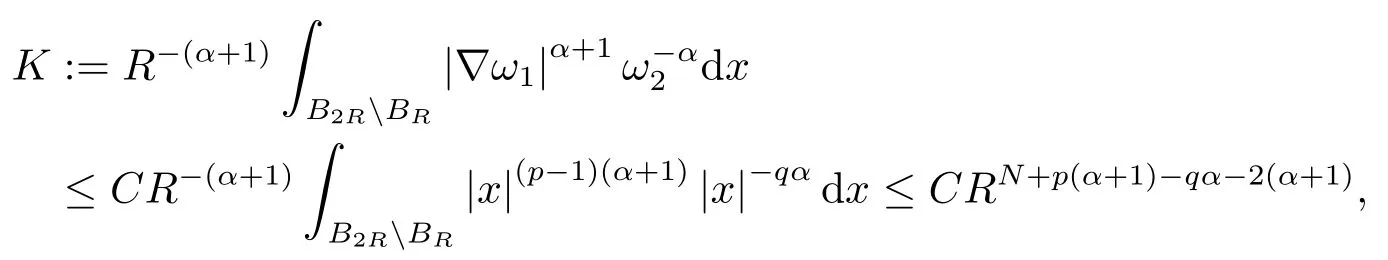
其中常数C＞0均不依赖于R.

再由定理2.2得到方程(1.1)不存在稳定解.推论2.3证毕.

下面，我们证明本文的第三个定理.

定理2.3的证明利用反证法.假设方程(1.1)存在稳定解u并类似于定理2.2的证明，我们取相同的ak(u)和bk(u)的函数.下面的证明将分为四个步骤展开.实际上，第一步到第三步的证明过程与定理2.2的证明相同，因此只给第四步的证明过程.

步4当|x|充分大，ω1(x)满足∇ω1(x)·x≤0，且对某个当R→∞时，J→0.则方程(1.1)不存在稳定解.

为了证明第四步，我们令R＞0且取ψ=ξm，其中m＞0待定，满足0≤ξ≤1，且

其中常数C不依赖于R且函数c(x)≥0.

由(4.6)式，我们有

其中常数C1，C2＞0仅依赖于α，m.

下面，估计(4.14)式右边两个积分项.对第一个积分，利用Hlder不等式，并取充分大的m满足m≥α+1，则我们得到

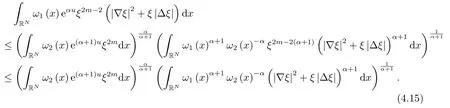
由∇(ω1(x))·x≤0且∇ξ=-c(x)·x，其中c(x)≥0，我们有

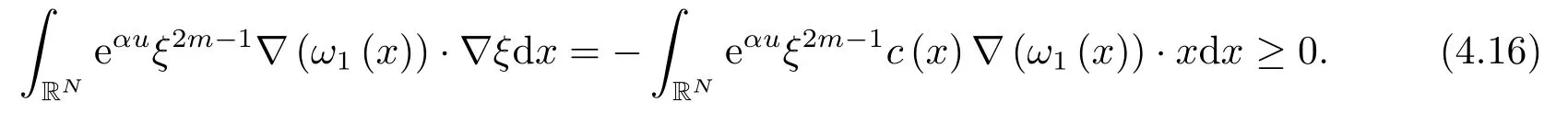
将(4.15)及(4.16)式代入(4.14)中，并利用ξ的性质，我们导出

且

利用条件:当R→∞时，J→0并在(4.17)式两边取R→∞极限，我们易知

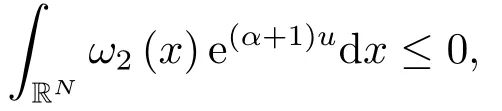
且导致矛盾.定理2.3证毕.

推论2.4的证明由假设ω2(x)∈L∞及当|x|充分大，有ω1(x)≤Cω2(x)，|∇ω1(x)|≤Cω2(x)知

知

推论2.5的证明由假设ω2(x)∈L∞及当|x|充分大，有ω1(x)≤Cω2(x)且∇ω1(x)·x≤0，我们得到