一道高考立体几何题的多维度剖析
王德玉+王圣敏
本文对2010年高考数学北京卷第16题第(3)问进行了多角度解析,方法比较独特,供大家在教學中参考.
原题如下:
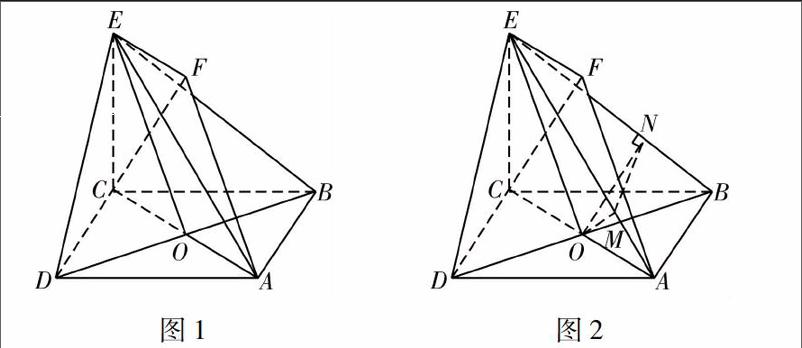
如图1,正方形ABCD和四边形ACEF所在的平面垂直,CE⊥AC,EF∥AC,AB=2,CE=EF=1.(1)求证:AF∥平面BDE;(2)求证:CF⊥平面BDE;(3)求二面角A-BE-D的大小.
解法1如图2,在△AOE中,作OM⊥OE,交AE于M.易知平面BDE⊥平面ACE,且平面BDE∩平面ACE=OE,所以,OM⊥平面BED.作ON⊥BE,连接MN,由三垂线定理知MN⊥BE,所以∠ONM为所求.易知DE=BE=3,BD=2,所以ON=613.在△AOM中,tan∠MAO=112,所以sin∠MAO=515,∠MOA=45°,由正弦定理得OM=213,所以tan∠ONM=OM1ON=313,所以∠ONM=30°.
解法2如图3,易知平面ACE⊥平面BDE,且平面ACE∩平面BDE=EO.延长EO,作AM⊥EO,则AM⊥平面BED.易知AB⊥平面BCE,所以,AB⊥BE.连接MB,由三垂线定理知∠MBA为所求.作FN⊥EO,易知FA∥EO,所以AM=FN,又EFOC为正方形,所以FN=212,所以sin∠MBA=AM1AB=21212=112,所以∠MBA=30°.
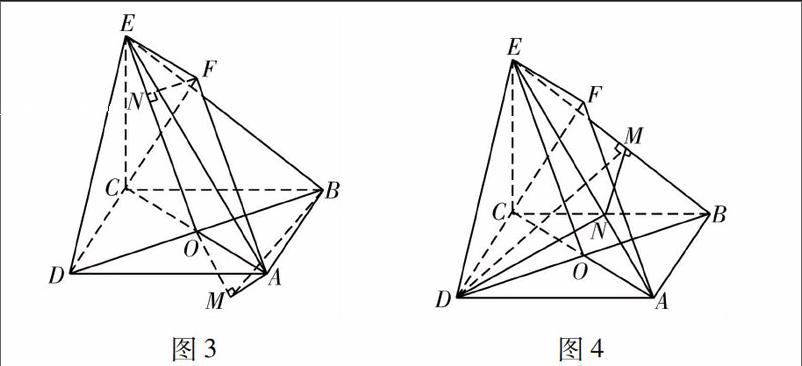
解法3如图4,作DM⊥BE,交BE于M,作MN∥AB,易知AB⊥BE,则MN⊥BE,则∠DMN为所求,连接DN,由等面积法知112BD·EO=112BE·DM,得DM=2613,又MN∥AB,得EM∶EB=MN∶AB,得MN=213,易知EN∶EA=1∶3,所以NA=2513,则cos∠ADE=1015.在△ADN中,由余弦定理得DN=1413.在△MND中,由余弦定理得cos∠DMN=312,所以∠DMN=30°.
解法4如图5,设点A到平面BDE的距离为h,则VA-BDE=VE-ABD,113S△BDE·h=113S△ABD·EC,得h=212.易知AB⊥平面BCE,得AB⊥BE,则二面角的正弦值为h1AB=112,所以二面角为30°.
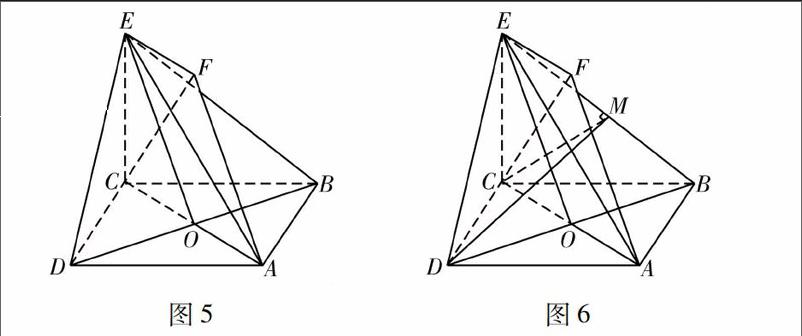
解法5如图6,设平面ABE与平面BCE所成的二面角为α,平面BDE与平面BCE所成的二面角为β,因为平面ABE∩平面BCE=BE,平面BDE∩平面BCE=BE,所以α-β为所求.作CM⊥BE,易知CD⊥面BCE,则连接DM,则tanβ=CD1CM=21613=3,β=60°.因为AB⊥平面BCE,所以ABE⊥平面BCE,所以α=90°,则α-β=30°.
图7解法6建立如图7所示空间直角坐标系,A(2,2,0),B(0,2,0),D(2,0,0),E(0,0,1).设平面ABE的法向量为n,易求n=(0,1,2),设平面BDE的法向量为m,易求m=CF=212,212,1,从而cos〈n,m〉=n·m1|n||m|=312,所以二面角为30°.
说明:前3种方法都是利用三垂线定理的方法来找二面角,其中法1和法3是构造直角三角形,法2是求垂线段的长时不关心位置,只关心长度;而法4是等体积法,法6是向量法,这两种方法较常见;法5是利用三个面中两两面成角的关系的方法.

