浅谈数学史在数学教学中的应用

巩诚+张天纲+李彦江+高翔宇

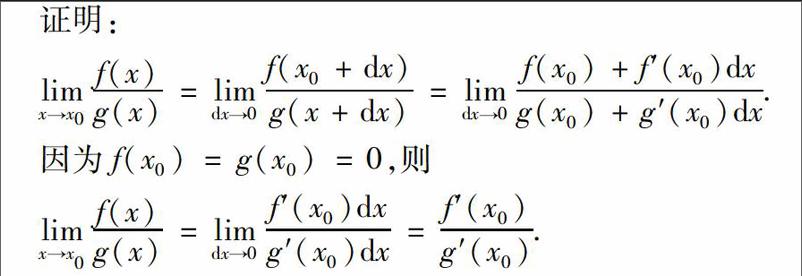
【摘要】本文通过追踪洛必达法则的历史，研究了洛必达法则在其发表时的证明方法问题，通过该问题的研究，让学生深刻理解了数学史在数学教学和学习中的重要意义，让学生更加深刻地理解了数学理论的意义，增加了学习兴趣.

【关键词】洛必达法则；数学史；微积分

【基金项目】黑龙江大学学位与研究生教育教学改革研究项目：数学史在研究生数学教学中的研究与应用；复杂四边形的几何约束求解方法，批准号：QL200702；黑龙江大学青年科学基金：QL200702；哈尔滨市科技创新人才专项资金项目：2016RQQXJ135.

数学史是研究数学发展历史的学科，数学史告诉我们，数学的发展并不合逻辑，也就是说数学发展的实际情况与我们今日所学的数学教科书很不一致.这就让刚刚接触高等数学的学生有很大的迷惑，或者产生误解.比如，我们知道洛必达法则的证明过程中应用了柯西中值定理，而洛必达（1661—1750）生活的时代要远远早于柯西（1789—1857），也就是说在洛必达法则发表的时代并没有出现柯西定理，那么洛必达先生是如何证明洛必达法则的呢？这是一个很容易引起学生迷惑的问题.对于本问题的澄清，也深刻地体现出数学史在数学教学和学习中的作用.在本文中，我们就深入探讨一下这个问题.在这里需要指出的是，有学者指出，洛必达法则更有可能是他的教师伯努利发现的，但是在这个问题上我们不做探讨，后面一致认为是洛必达.

下面我们首先给出洛必达法则.

洛必达法则（1696年，010型未定式）：设函数f（x）和g（x）在点x0的某去心邻域Uo（x0）内可

洛必达法则最早出现在1696年出版的《基于无限小的曲线分析》一书中，而柯西中值定理则出现在19世纪前期，比洛必达法则晚100多年.柯西中值定理表述如下：

柯西中值定理（19世纪前期）：设函数f（x）和g（x）分别在闭区间[a，b]连续，在开区间（a，b）可导，并且g′（x）≠0，则在开区间（a，b）内至少存在一点ξ，使得

f′（ξ）1g′（ξ）=f（b）-f（a）1g（b）-g（a）.

我们知道，柯西中值定理是拉格朗日中值定理的推广，是微分学的基本定理之一.其几何意义为，用参数方程表示的曲线上至少有一点，它的切线平行于两端点所在的弦.该定理可以视作在参数方程下拉格朗日中值定理的表达形式.拉格朗日中值定理是由法国数学家拉格朗日于1797年在其著作《解析函数论》的第六章中提出的，并进行了初步证明.其形式如下：

拉格朗日中值定理（1797年）：设函数f（x）在闭区间[a，b]连续，在开区间（a，b）可导，则在开区间（a，b）内至少存在一点ξ，使得f′（ξ）=f（b）-f（a）1b-a.

拉格朗日中值定理提供了用导数来研究函数的依据，它是微分学的基本定理之一.同时，它又是罗尔定理的推广，其证明过程的关键一点是应用了罗尔定理.

罗尔中值定理（1691年）：设函数f（x）在闭区间[a，b]连续，在开区间（a，b）可导，且f（a）=f（b），则f′（x）在开区间（a，b）内至少有一个零点，即至少存在一点ξ∈（a，b），使得f′（ξ）=0.

由此，我们追踪洛必达法则的历史渊源，可知罗尔中值定理（1691年）这个基础性定理比洛必达法则（1696年）要早5年.那么问题来了，难道是洛必达基于罗尔中值定理将拉格朗日中值定理和柯西中值定理一一推导出来，然后仅仅发表了洛必达法则？这显然是不可能的.那么，洛必达又是如何证明的呢？

我们再环顾一下洛必达法则发表的时代，看看当时的数学理论发展到什么程度.我们知道微积分是由牛顿和莱布尼茨分别独立创立的，结合牛顿和莱布尼茨二者的工作，从时间上来看，牛顿发现微积分理论要早于莱布尼茨，但是莱布尼茨对微积分理论的发表要早于牛顿，其于1684年发表第一篇微分论文，定义了微分概念，采用了微分符号dx，dy.1686年他又发表了积分论文，讨论了微分与积分，使用了积分符号∫.

最早发表的微积分理论仅仅比洛必达法则早了12年，这段时间是微积分理论的初创期，很多结论并不完善，也不严密，所以洛必达法则产生于这样一个时代基础之上，其结论是划时代的（由柯西中值定理可窥一二），其证明过程也不可能太严密，或者说根本就不严密.那么洛必达到底是如何证明的呢？我们想一下，莱布尼茨早期所发表的微积分理论到底告诉我们了什么呢？他告诉我们的当然是牛顿-莱布尼茨公式，也就是：

牛顿-莱布尼茨公式（1686年）：设函数f（x）在闭区间[a，b]内连续，F（x）为f（x）的一个原函数，则

稍做转化，这个基本的微积分公式所表达的含义可以有如下形式：

显然，洛必达完全可以看到这一步.有学生要质疑了：“不对啊，公式（1）是通过积分中值定理得到的.”这样想是错误的，因为这个公式是牛顿和莱布尼茨最早发现的，那个时候中值定理根本就没出现，这只是我们的教材上的证明方法.至于当时牛顿-莱布尼茨公式是如何得到的，这个问题和本文讨论的问题类似，并没有严格的数学证明，这些都是牛顿他们通过相对简单的数学推导和深刻的数学直觉得到的.

那么我们利用式（1）来证明洛必达法则.

证明：

我们今日中学所学的数学内容基本上属于17世纪微积分学以前的初等数学知识，这些数学教材业已经过千锤百炼，是在科学性与教育要求相结合的原则指导下经过反复编写的，這样就必然舍弃了许多数学概念和方法形成的实际背景、知识背景、演化历程以及导致其演化的各种因素，因此，仅凭数学教材的学习，难以获得数学的原貌和全景，同时忽视了那些被历史淘汰掉的，但对现实科学或许有用的数学材料与方法，而弥补这方面不足的最好途径就是通过数学史的学习.

本文通过追踪洛必达法则的证明过程，充分显示了数学史在数学教学和学习中的重要作用，加深了对相应数学定理的理解，增加了学习兴趣.

【参考文献】

[1]刘艳滨，于菂，肖相武.高等数学（上）[M].哈尔滨：黑龙江大学出版社，2012.

[2]张玲.单因素及双因素方差分析及检验的原理及统计应用[J].数学学习与研究，2010（7）：92-94.

[3]吴珊.数学史在大学数学教学中的应用[J].吉林教育，2009（10）：15-16.

[4]余井权、曹治清、王海燕，数学史在高等数学教学中的应用体会[J].成都中医药大学学报（教育科学版），2012（1）：44-45.

[5]欧阳跃.数学史在数学教学中的作用[J].曲靖师范学院学报，2002（6）：35-37.