一个数论函数方程的可解性

李昌吉

（阿坝师范学院藏汉双语学院，四川汶川 623002）

1 引理

2 定理及其证明

定理1方程

的所有正整数解是n=17,31,32,37,65,69,77,91,93,94,95,99,104,111,112,115,117,118,122,124,135,142,144,146,148,152,178,184,188,216,195,231,238,260,273,280,285,286,306,308,310,312,315,318,336,350,360,364,366,370,372,380,396,418,434,438,444,450,456,460,468,470,504,540,558,594,714,770,780,840,858,910,924,930,990,1050,1092,1110,1140,1170,1254,1260,1302,1386,2310,2730,共86组。

1）若ω(n)≥4即k ≥4时，因为m 是正整数，则有m ≥27，易知ω(m)≥8。由引理1，

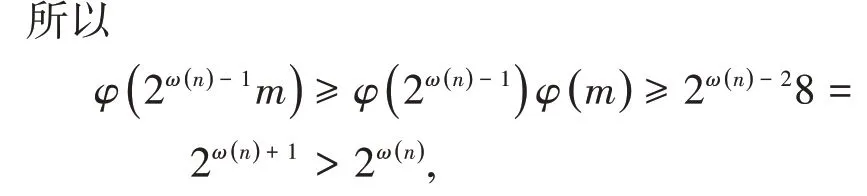
所以方程（2）无解，即方程（1）无解。

2）当ω(n)=3即k=3时，方程（2）化为φ(4m)=16，易知4m=17,32,34,40,48,60。因为m，t 是正整数，所以t=24,30,36,45。因为(-1)Ω(n)=±1，

经检验，不存在pi，ai(1 ≤i ≤3)满足条件成立，所以此时方程（1）无解；

ii）若t=30,36 时，同理检验，不存在pi，ai(1 ≤i ≤3)满足条件成立，所以此时方程（1）无解；

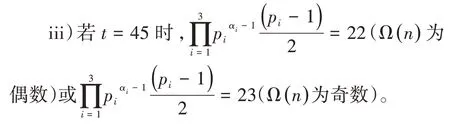
经检验，p1=2，p2=5，p3=23，a1=2，a2=a3=1与p1=2，p2=5，p3=47，a1=a2=a=1 满足条件，所以此时方程（1）的解为n=460，470。

3）当ω(n)=2即k=2时，方程（2）化为φ(2m)=8，易知2m=15,16,20,24,30。因为m，t 是正整数，所以4m=24,30,36,45。因为(-1)Ω(n)=±1,

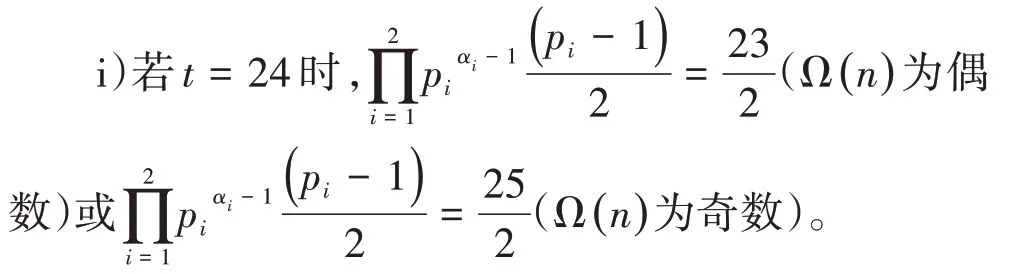
经检验，p1=2，p2=47，a1=a2=1满足条件，所以此时方程（1）的解为n=94；

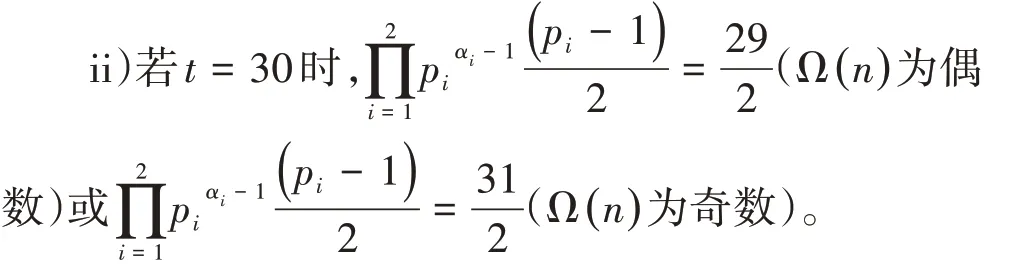
经检验，p1=2，p2=59，a1=a2=1满足条件，所以此时方程（1）的解为n=118；

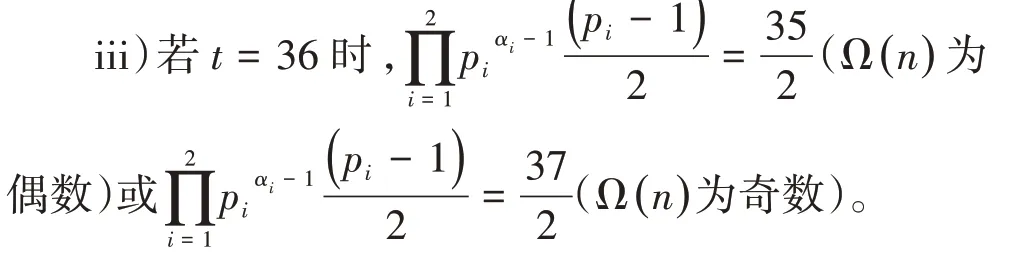
经检验，p1=2，p2=71，a1=a2=1满足条件，所以此时方程（1）的解为n=142；

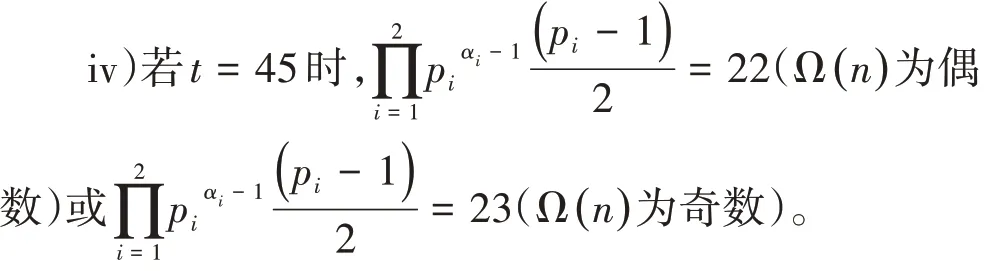
经检验，p1=5，p2=23，a1=a2=1 或p1=2，p2=89，a1=a2=1 或p1=2，p2=23，a1=3，a2=1或p1=2，p2=47，a1=2，a2=1 满足条件，所以此时方程（1）的解为n=115,178,184,188。

4）当ω(n)=1即k=1时，方程（2）化为φ(m)=4，易知m=5,8,10,12。因为m，t 是正整数，所以t=15，24，30,36。因为(-1)Ω(n)=±1，

经检验，p1=17，a1=1 或p1=2，a1=5 满足条件，所以此时方程（1）的解为n=17，32；

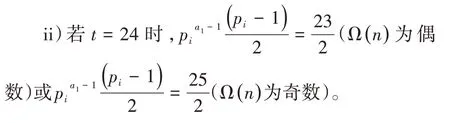
经检验，不存在p1，a1满足条件成立，所以此时方程（1）无解；

iii）若t=30，36 时，同理经检验，不存在p1，a1满足条件成立，所以此时方程（1）无解。

情况2

经检验，不存在pi，ai(1 ≤i ≤3)满足条件成立，所以此时方程（1）无解。

3）当ω(n)=3即k=2时，方程（3）化为φ(2m)=16，易知2m=17,32,34,40,48,60。因为m 是正整数，t 是正奇数，所以t=51，即

经检验，p1=2，p2=53，a1=1，a2=1满足条件，所以此时方程（1）的解为n=318。

4）当ω(n)=2即k=1时，方程（3）化为φ(m)=8，易知m=15,16,20,24,30。因为m是正整数，t是正奇数，所以t=45，即

经检验，p1=23，a1=1 满足条件，所以此时方程（1）的解为n=69。

1）若ω(n)≥6 即k≥6 时，有m ≥60，易知此时φ(m)≥16。由引理1，

3 结论

研究了含有复合广义Euler 函数的不定方程φ2(φ3(n))=2ω(n)，其中n 为正整数，结合广义Euler 函数φ2(n)和φ3(n)的性质，利用初等方法进行分类讨论，给出方程φ2(φ3(n))=2ω(n)的全部86组正整数解。