ESPCPs推力球轴承接触问题有限元分析

卢立河，王世杰

（沈阳工业大学机械工程学院，辽宁沈阳 110870）

潜游螺杆泵转子反馈的轴向载荷均由置于球铰型自动调心联轴体[1]中的推力轴承承受，根据现阶段数据统计，系统轴向力的总和为50～120 KN不等[2]，且随着螺杆泵采油系统下潜深度等进一步的增加，施加在推力轴承上的轴向力也将随之增加[3]，因此轴承的疲劳寿命将面临着高负载严峻考验，可见推力轴承的使用工况苛刻，导致现行标准轴承的使用寿命短。

由于井下机组部分维护、维修困难，成本较高且系统零部件的寿命均具有“短板效应”，一旦轴承发生失效，必然导致井下机组的使用寿命降低，系统整体使用寿命也将随之降低，这将大大影响系统的推广与使用，同时其他部件也因提前更换而导致成本的增加；从等寿命及可靠性原则的角度上考虑，轴承寿命是决定系统整体使用寿命的关键[4]。文章通过Hertz 弹性接触理论解和有限元仿真计算结果的对比，分析轴承在载荷作用下的接触问题。

1 Hertz弹性接触理论

Hertz 弹性接触理论[5]，作了以下假设，成功地解决了滚动轴承接触应力、变形的计算问题，这些假设对于滚动轴承内部的接触问题而言是基本上成立的。

（1）材料是均质的；

（2）接触区的尺寸远远小于物体的尺寸；

（3）作用力与接触面垂直（假设接触区域无摩擦）；

（4）变形在弹性极限内进行。

由Hertz 理论可知，主曲率和函数及主曲率差函数如公式(1)、(2)所示。

主曲率和函数∑ρ：

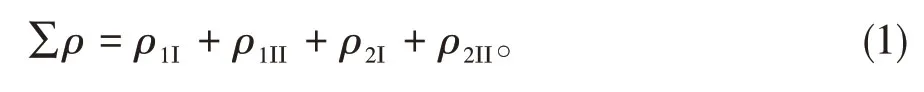
主曲率差函数F(ρ)：

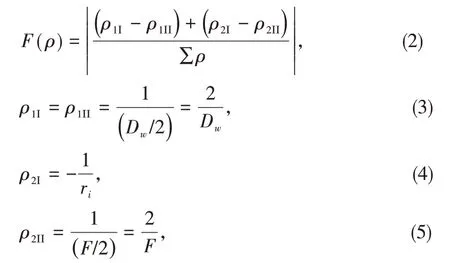
式中：ρ1I、ρ1II为球型滚动体在两个主平面上的曲率；ρ2I、ρ2II为轴圈、座圈内滚道在两个主平面上的曲率；Dw为球型滚动体直径；ri为沟道曲率半径。

椭圆接触面的长半轴、短半轴长度分别为a、b，弹性趋近量为δ，计算公式如(6)、(7)、(8)所示：

式中：σ、v、ω为椭圆接触区尺寸系数；E1、E2为轴承滚动体和滚道的弹性模量；μ1、μ2为轴承滚动体和滚道的泊松比；Q 为推力球轴承滚动体承受的轴向载荷，一般情况下指承载最大载荷的滚动体：

式中：Fa为施加于轴承的外部轴向载荷；Z 为滚动体数目；α为承载时的接触角（°）。

由于公式(6)、(7)、(8)求解繁琐，重复性计算大大增加了工作量。由于本文所研究的推力球轴承型号为51410，材料为轴承钢GCr15，在工程上可使用经帕姆格林（A.Palmgren）优化计算式简化后的公式进行求解，大大缩减了工作量，且计算所得数据相等，这是因为滚动轴承的材料一般为轴承钢，可见经简化后的公式十分便于求解，公式(10)、(11)、(12)即为椭圆接触面长、短半轴、弹性趋近量经帕姆格林优化计算后的公式：

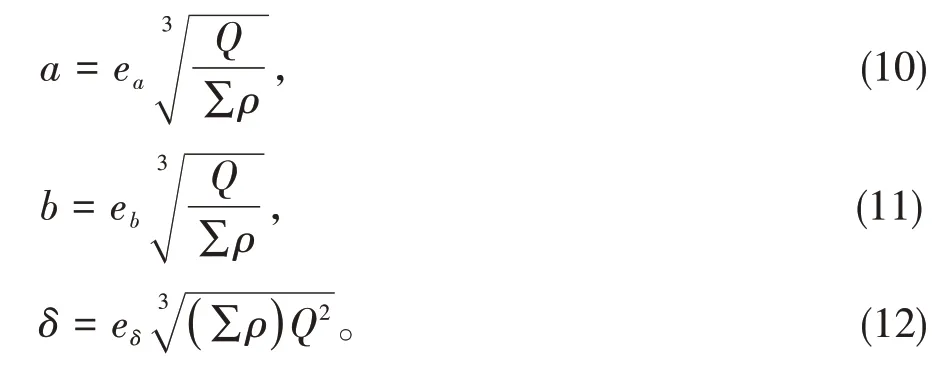
根据以上公式推导，经简化后的赫兹接触应力计算公式如(13)、(14)所示。

最大赫兹接触应力：

平均赫兹接触应力：

选取的轴承为现行标准下的推力球轴承51410，其相关参数如表1所示。

表1 51410推力球轴承相关参数

根据上述公式计算方法，将表中相关参数代入公式（3）、（4）、（5）、（9）可得；

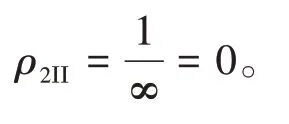
将上述数据代入公式（1）、（2），因此主曲率和函数及主曲率差函数为：

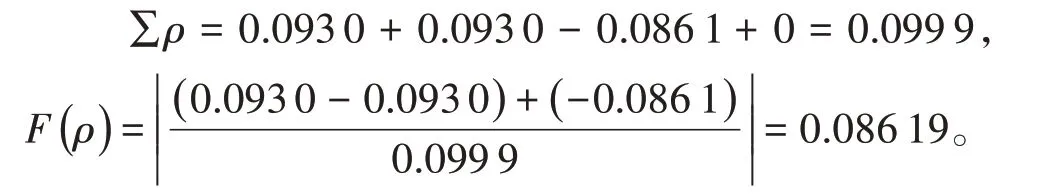
由上述计算结果可知，F(ρ)=0.8619 ≈0.086，查赫兹接触系数表[5]，得出如表2数据。

表2 赫兹接触系数（E=207GPa，μ=0.3）

通过上述表2可查得，ea=0.063 30，eb=0.01178，πeaeb=2.342 × 10-3，a/b=5.38，eδ=2.047 × 10-4。

将以上数据带入公式（10）、（11），可求得接触椭圆的长半轴a及短半轴b分别为：

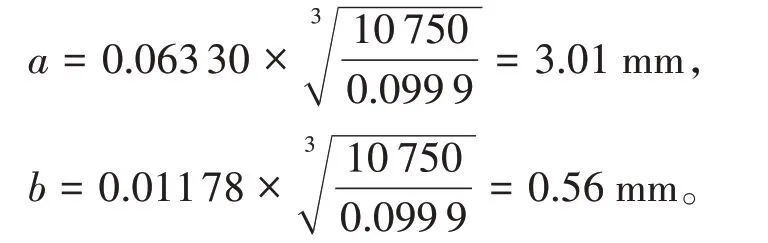
因此，接触椭圆的长轴和短轴分别为2a=6.02 mm，2b=1.12 mm，由公式(13)求得推力球轴承滚动体最大接触应力：

由公式(14)求得推力球轴承滚动体的平均接触应力为：

由公式(12)求得推力球轴承滚动体的弹性趋近量为：

将赫兹弹性接触理论计算得出的推力球轴承滚动体最大接触应力理论解与有限元数值分析仿真计算的结果进行对比，分析有限元仿真分析结果与赫兹弹性接触理论计算结果的差异性。

2 轴承应力有限元分析

（1）轴承模型的构建及网格的划分

选取的轴承为现行标准下的推力球轴承51410，其几何特征参数如表3所示。

表3 推力球轴承几何参数

考虑到推力球轴承是轴对称结构，选取轴承整体的1/Z（Z 为滚动体数目）作为分析对象，即选取轴承整体的1/8 作为分析对象，在Creo 三维软件建立51410 推力球轴承的几何模型，根据圣维南定理[6]进行模型简化，在建模时忽略圆角、游隙等因素；同时为了建模方便，节约计算资源，忽略保持架对有限元分析结果的影响[7-8]，推力球轴承51410三维模型如图1所示。

图1 51410轴承模型

在Creo软件中导出51410三维几何模型，另存命名为51410.stp 格式，再导入到Ansys Workbench 仿真软件中，首先材料设置为高碳铬轴承钢GCr15，其参数如下表4所示。

表4 推力球轴承材料参数

由于导入的模型粗糙不便于计算求解，此时需要对模型进行拓扑优化处理；由于软件无法自动识别导入的模型为1/8，此时需要自行对轴承模型进行设置轴对称，可以采取新建Cylindrical 圆柱坐标系，利用Symmetry 功能设置轴对称，在此基础上用网格划分功能自动生成网格，单元类型选择为8 节点solid45号单元，为提高数值计算精度，需要细化网格，由于接触是非线性问题，若是将整体进行网格细化，其计算占用的资源相当大，为节省计算机资源的同时提高效率，可以采用局部细化接触区域网格的方法，即仅将滚动体与轴圈、座圈滚道面接触处网格进行局部细化，可采用软件自带的contact sizing 进行网格细化，共划分662 384 个网格单元,生成1 003 477 个节点，模型网格划分如图2所示。

图2 网格划分

（2）接触对的设置

多零件表面发生接触时，需要指定接触对中的目标面和接触面，由于滚动体表面为凸面，滚道面为凹面，因此设置滚动体表面为接触面，轴圈、座圈滚道面为目标面[9]，设置滚动体与轴圈、座圈滚道面接触类型为Frictional，在考虑良好的脂润滑条件下设置摩擦系数为0.1。

（3）载荷与约束的施加

根据轴承的实际工况进行模拟，因此轴承座圈底部施加固定约束，由于模型为原来的1/8，因此轴圈顶部模拟轴施加轴向载荷数值也为初始载荷的1/8，即10 750 N，如图3所示。

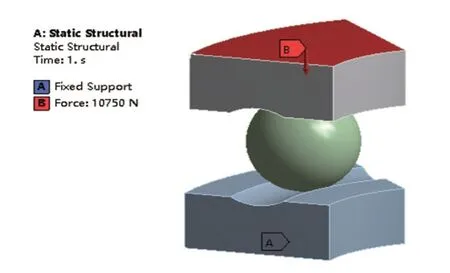
图3 载荷与约束

（4）有限元分析计算结果

经Ansys Workbench 仿真软件分析计算得51410推力球轴承的等效应力云图，如图4 所示。从图4 明显可以看出，推力球轴承的等效应力主要集中在滚动体与轴圈、座圈滚道面接触区域，此时最大接触等效应力值为2 947.2 MPa。

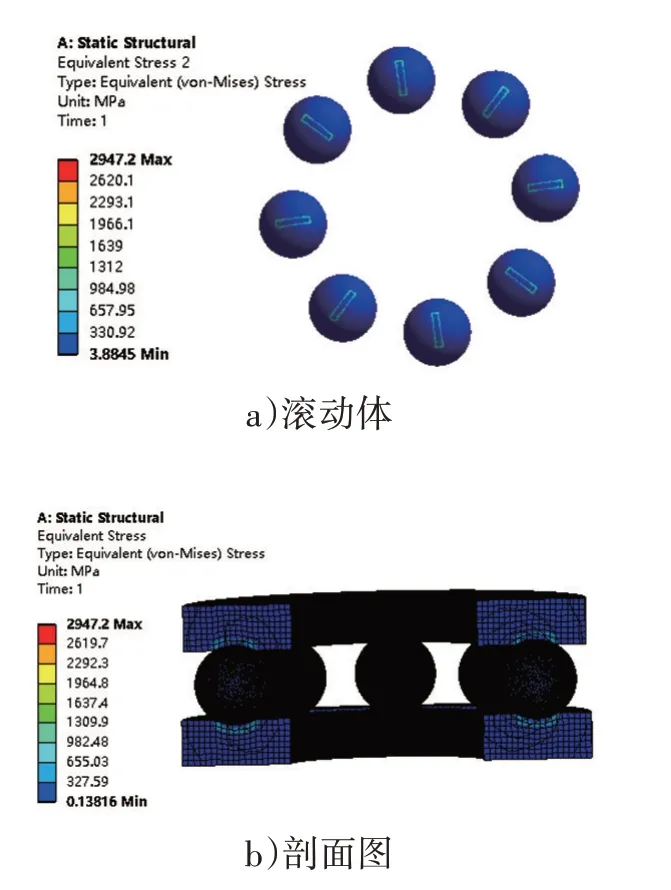
图4 51410等效应力云图

3 结果分析

根据赫兹理论解可知，滚动体局部的接触应力高达3 043 MPa，有限元仿真得出的滚动体局部的接触应力也高达2 947.2 MPa，可见理论解与计算结果仅相差2%，当然这主要也是软件参数设置得当，与理论解偏差较小，说明二者具有良好的一致性，验证了采用数值模拟手段分析轴承在载荷作用下的接触应力是符合实际情况。

此外，由理论解及仿真计算结果显然可见滚动体局部的接触应力非常大，这是因为滚动体与滚道间的接触载荷只作用在非常小的接触面上，而接触面经过网格局部细化，导致接触面被划分为诸多微小面，因此即使施加的接触载荷不是很大，最大接触应力值也是相当高的。

从轴承钢GCr15 的材料屈服极限为518.42 MPa可知，仿真计算的最大应力值已经远远超过了材料的屈服极限，势必导致轴承失效，但是接触应力存在于非常小的局部区域内，即便是计算的接触应力值超过材料的屈服极限，也仅会在有限的局部区域内发生塑性变形[10]，产生塑性变形后接触面积变大，接触应力也会瞬间减小到材料的屈服强度以内。

4 结语

通过Hertz弹性接触理论解和有限元仿真计算结果的对比分析，得出以下结论：

（1）采用数值分析模拟手段及Hertz 弹性接触理论计算方法分别对推力球轴承51410 进行了接触问题的分析计算，对比分析得出二者的计算结果误差小，具有良好的一致性，因此采用数值模拟手段分析轴承在载荷作用下的接触应力是符合实际情况。

（2）有限元数值模拟手段对比Hertz 理论解优点是：考虑了接触处的摩擦，更符合轴承应用的实际工况，并且可以直观地查看各个部位的数据，因此仿真计算结果相对更具有工程实用价值。

（3）仿真计算结果为分析潜油螺杆泵采油系统中的推力球轴承的实际工况提供了一种方案，也为今后滚动轴承的失效分析及优化设计提供了一种有效的参考依据。

（4）滚动轴承的有限元仿真分析本质上是复杂多学科综合应用的工程，参数设置略有偏差导致所得的计算结果差异性很大，诸如网格划分、边界问题及约束等设置需反复验证，确保计算结果的准确性。