A New Class of Estimators for Extreme Value Index

CHANG Shuai(常帅)

(Department of Mathematics，Taiyuan Normal University，Jinzhong 030619，China)

Abstract:In this paper，a new class of extreme value index(EVI)estimators as a generation of the Hill estimator is proposed.Under the first-order condition and secondorder condition，we prove that the introduced estimators are consistent and asymptotically normal.Although new EVI-estimators and Lp EVI-estimators have the same asymptotic behaviour，the form of new EVI-estimators is simple.And the performance of new EVI-estimators is slightly better than that of Lp EVI-estimators at the same level in the finite samples.Meanwhile，we compare new EVI-estimators with moment estimator and mixed-moment estimator in the optimal level by means of Monte-Carlo simulation.It is concluded that new EVI-estimators have a better competitiveness.

Key words:Heavy-tailed;EVI-estimator;Second-order condition;Asymptotic normality

1.Introduction

Statistics of univariate extremes has important practical application，like stock returns in finance，large claim in insurance，waiting time in telecommunications and among others.One of the topical issues is the estimator of the extreme value index(EVI)，a primary parameter that measures essentially the weight of the tail of a distribution.The topic has been dealt with in many papers.

Suppose a sample of sizenof independent，identically distributed(IID)random variables，X1，···，Xn，with a cumulative distribution function(CDF)F.Let us consider the notationX1，n，···，Xn，nfor the associated ascending order statistics.If there exist real constantsan＞0 andbn∈R such thatP(Xn，n≤anx+bn)=Fn(anx+bn)→EVγ(x)，asn→∞，where EVγ(x)is the general extreme value(EV)CDF[1]，given by

we say that the CDFFbelongs to the max-domain of attraction of EVγin(1.1)，and use the notationF∈DM(EVγ).The parameterγis the EVI，the primary parameter of extreme events.Ifγ＞0，the right-tail function(RTF)defined by:=1-F(x)is heavy，of a negative polynomial type andFhas an infinite right endpoint.It is well-known that the positive EVI measures the heaviness of RTF and the heavier the RTF is，the largerγis.We writeF←(x):=inf{y:F(y)≥x}for the generalized inverse function ofF，U(t):=for the reciprocal tail quantile function(RTQF)ofFandRαfor the class of regularly varying functions at infinity with an index of regular variation equal toα∈R，i.e.，positive measurable functionsg(·)such thatg(tx)/g(t)→xα，ast→∞，for allx＞0.[2]Ifγ＞0，then

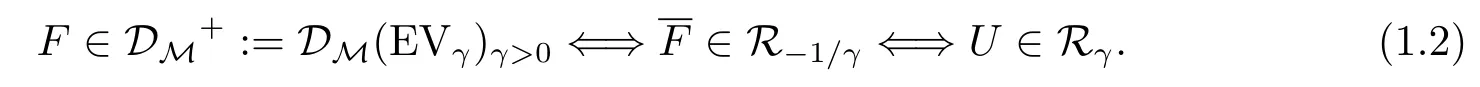
In this paper we mainly work with a Pareto-type(heavy-tailed)models underlying CDF in(1.2)which is known as the first-order condition(FOC).However，a FOC is in general not sufficient to study properties of EVI-estimators，in particular for asymptotic normality.In that case，a second-order condition(SOC)is required by ruling the rate convergence of the FOC in(1.2).It is the following

which is valid for everyx＞0，whereρ≤0 is a second-order parameter and|A|∈Rρ.[3]

EVI-estimators have been considered in many papers.For Pareto-type models，the classical EVI-estimator is the Hill(H)estimator[4]，which is the averages of the log-excessesVikor of log-spacingsUi，i.e.，

where

An alternative estimator so called the moment(M)EVI-estimator is proposed by Dekkers et al.[5]forγ∈R and has the following form

Based on the H estimator in(1.4)，the generalized Hill(GH)EVI-estimator is proposed by Beirlant et al.[6]，and is defined as

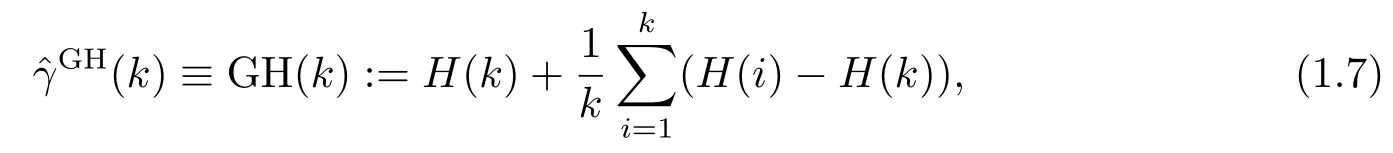
whereH(k)is in(1.4)，and further study is in[7].

We consider the ML EVI-estimator proposed by Drees et al.[8]，given by

which is valid forγ＞-1/2，whereis the implicit ML estimator of the unknown scale parameterα，and further study is done in[9-10].

Just as in[11]，we also consider the generalized Pareto probability weighted moments(GPPWM)EVI-estimator，that is，

which is valid forγ＜1，withk=1，2，···，n-1，and

As an revisited GPPWM estimator in[12]，the PPWM EVI-estimator is defined by

which is valid forγ＜1，withk=1，2，···，n-1，andj=0，1，and further study is done in[13].

We further refer to the so-called mixed-moment(MM)EVI-estimator in[14]，valid forγ∈R and given by

On the basis of the fact that H estimator in(1.4)is the logarithm of the geometric mean of

Brilhante et al.[15]considered the power mean，also known as Hlder’s mean-of-order-p(MOP)，of(1.12)，leads to

whereUikin(1.12)，H(k)in(1.4).

Recently，based on Lehmer’s mean-of-order-pPenalva et al.[16]proposed the class of Lehmer’s mean-of-order-p(Lp)EVI-estimators，i.e.，

LpEVI-estimators have been compared with the aforementioned EVI-estimators in the asymptotic behaviour and have better performance in a certain range.But a finite sample behavior ofLpEVI-estimators hasn’t been studied.In this paper，we compare new EVIestimators in(2.1)withLpEVI-estimators in the finite sample.

The rest of the paper is organized as follow.In Section 2，a new class of EVI-estimators is proposed and we formulate the main results of the paper and give the proofs.In Section 3，we compare new EVI-estimators withLpEVI-estimators by Monte Carlo simulation at the same level.Furthermore，the new EVI-estimators are also compared with the H，M，MM estimators in the optimal level.In the last section，there are formulated conclusions.

2.New EVI-estimators

In this section，a new class of EVI-estimators，so-calledNαEVI-estimators，is proposed by

We now state the main results，which establish the consistency and asymptotic normality of theNαEVI-estimators.

Theorem 2.1Under the validity of the first-order condition in(1.2)，and for intermediate sequencesk，i.e.，sequences of integer valuesk=k(n)，1≤k＜n，such that theNαEVI-estimators in(2.1)are consistent for the estimation ofγ，provided that we work inSNα={(γ，α)|γ＞0，α≥0}.Under the second-order conditions in(1.3)，the asymptotic distributional representation of theNαEVI-estimators is

To prove Theorem 2.1，we need a lemma.

Lemma 2.1[17]LetE1，···，Endenote independent standard exponential random variables.Under the validity of(1.2)，(1.3)and(2.2)，then there exist random variablesRj，n，such that

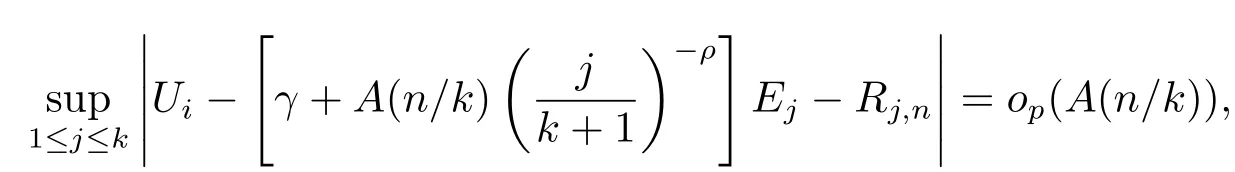
whereUiin(1.5)，and

Next，we give the proof of Theorem 2.1.

ProofDenote:=Kαand by Lemma 2.1，we have

Hence，we get

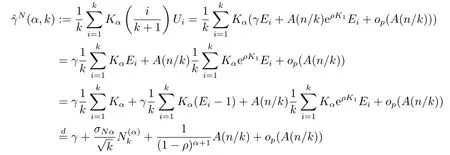
The proof is completed.

Remark 2.1The component of asymptotical biasbNαindependent ofγis always smaller than 1，and is decreasing inα≥0.And we have

On the other hand，the asymptotical standard deviationσNαdependent ofγis increasing inα≥0.Such a performance is shown in Figure 2.1.

Fig.2.1 Plots of bNα，for ρ=-0.1，-0.5，-1 and-2，and of σNα，for γ=1，as functions of α≥0

Remark 2.2AlthoughbNαandσNαof new EVI-estimators are same as that of Lp+1EVI-estimators，the form of new EVI-estimators is simple.So asymptotic comparison of new EVI-estimators at optimal levels is similar to that of LpEVI-estimators(see[16]).

Next，we mainly study the performance of new EVI-estimators in the finite samples.

3.Finite Sample Behaviour of New EVI-Estimators

We have run a small-scale Monte Carlo simulation，on the basis ofN=100 runs，for a sample sizen=1000，from the following underlying models:

1)the Fr´echet(γ)model with CDFF(x)=exp(-x－1/γ)，x≥0，ρ=-1;

2)the Burr(γ，ρ)model with CDFF(x)=1-(1+x－ρ/γ)1/ρ，x≥0.

For each of the aforementioned models，we have simulated the mean values(E)and mean squared errors(MSE)of the estimators as functions of the number of top order statisticskinvolved in the estimation.

Firstly，we compare NαEVI-estimators with Lp+1EVI-estimators(Lp+1:=for short)at the same levels.For Fr´echet(1)and Burr(1，-1)models，we picture the E and MSE of NαEVI-estimators andEVI-estimators forα==0.5 and 1 respectively in Figs.3.1-3.4.We can see that the performance of NαEVI-estimators is slightly better than the performance ofEVI-estimators，although they have the same asymptotic behaviour.

Secondly，we compare NαEVI-estimators with H，M and MM EVI-estimators in the optimal level.The optimal levelα*is defined asα*:=arg minα≥0MSE(Nα(k)).For simplicity，the optimal NαEVI-estimators are denoted by N*.For Burr(γ，-1)，γ=0.25，0.5，1 and 2 models，we picture the E and MSE of N*，H，M and MM EVI-estimators respectively in Figs.3.5-3.8.For Burr(0.25，-1)model，as asymptotic behaviour，N*EVI-estimators work best in all of mentioned EVI-estimators.For Burr(0.5，-1)model，the performance of N*EVIestimators is worse than that of M EVI-estimator，because M EVI-estimator is an asymptotic unbias estimator inγ-γρ+ρ=0.But whenkis small(k＜400)，N*EVI-estimators work well.For Burr(1，-1)model，the performance of N*EVI-estimators is better than that of M EVI-estimator，but not as good as MM EVI-estimators，because MM EVI-estimator is an asymptotic unbias estimator inγ+ρ=0.For Burr(2，-1)model，the performance of N*EVI-estimators is obviously best.

As expect，none of the EVI-estimators dominate all the others，but new EVI-estimators have a better competitiveness in practice.

Fig.3.1 Mean values(left)and mean squared errors(right)of H，N0.5 and L0.5 estimators，for samples of size n=1000 from a Fr´echet(1)model

Fig.3.2 Mean values(left)and mean squared errors(right)of H，N1 and L1 estimators，for samples of size n=1000 from a Frchet(1)model

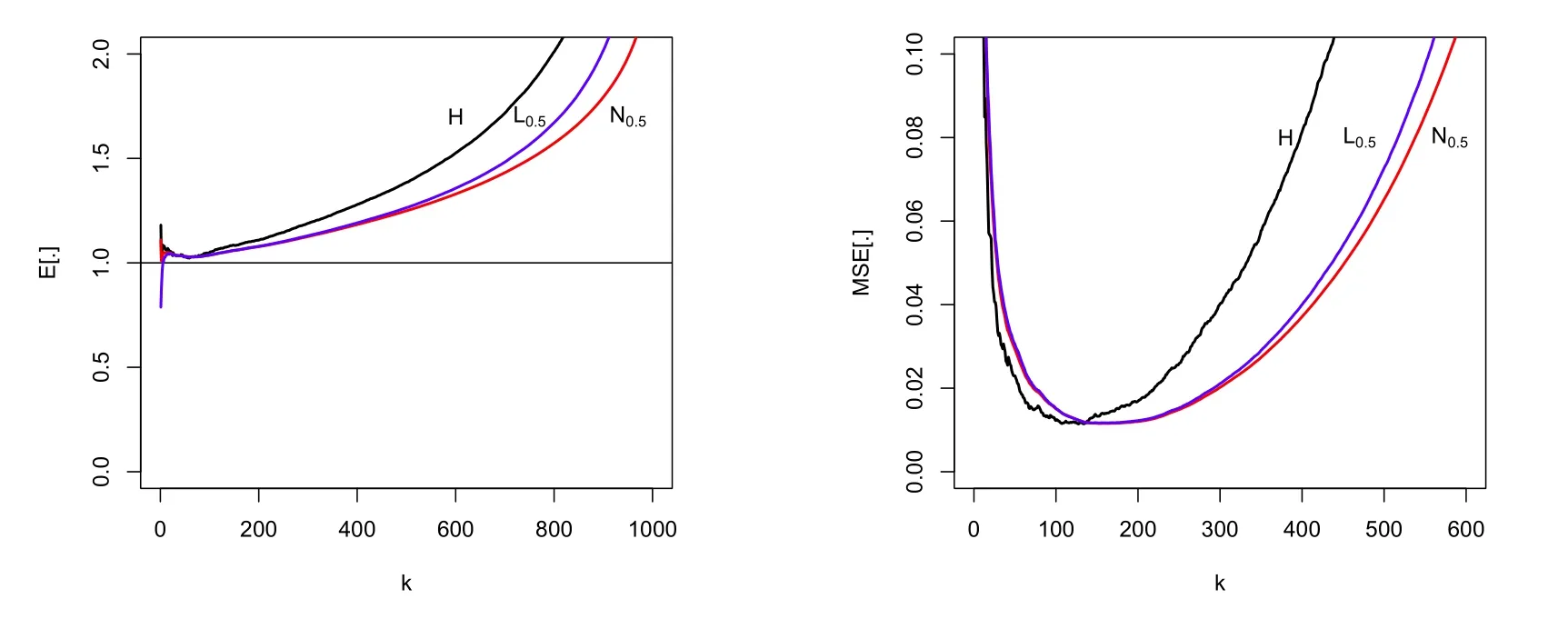
Fig.3.3 Mean values(left)and mean squared errors(right)of H，N0.5 and L0.5 estimators，for samples of size n=1000 from a Burr(1，-1)model

Fig.3.4 Mean values(left)and mean squared errors(right)of H，N1 and L1 estimators，for samples of size n=1000 from a Burr(1，-1)model

Fig.3.5 Mean values(left)and mean squared errors(right)of H，M，MM and N*estimators，for samples of size n=1000 from a Burr(0.25，-1)model

Fig.3.6 Mean values(left)and mean squared errors(right)of H，M，MM and N*estimators，for samples of size n=1000 from a Burr(0.5，-1)model

Fig.3.7 Mean values(left)and mean squared errors(right)of H，M，MM and N*estimators，for samples of size n=1000 from a Burr(1，-1)model

Fig.3.8 Mean values(left)and mean squared errors(right)of H，M，MM and N*estimators，for samples of size n=1000 from a Burr(2，-1)model

4.Conclusions

For heavy-tailed models，a new class of EVI-estimators is proposed.Under the first-order condition and second-order condition，we prove that the introduced EVI-estimators are consistent and asymptotically normal.Although new EVI-estimators andLpEVI-estimators have the same asymptotic behaviour，the form of new EVI-estimators is simple.For finite samples，the performance of new EVI-estimators is slightly better than that ofLpEVI-estimators.Meanwhile，we compare new EVI-estimators with moment estimator and mixed-moment estimator in the optimal levels.Some simulation results show that new EVI-estimators have a better competitiveness.