A Line Search Method with Dwindling Filter Technique for Solving Nonlinear Constrained Optimization
PEI Yonggang(裴永刚),KONG Weiyue(孔维悦),DONG Lanting(董兰婷)
(Engineering Laboratory for Big Data Statistical Analysis and Optimal Control,College of Mathematics and Information Science,Henan Normal University,Xinxiang 453000,China)
Abstract:In this paper,a different line search filter algorithm is proposed for solving nonlinear equality constrained optimization.The optimality condition of the nonlinear optimization problem is regarded as a new filter pair which is embedded in the backtracking line search framework.By adding a dwindling function to the step acceptance criteria,the thickness of the filter’s envelope is getting smaller and smaller when the step size decreases.So the line search trial step size in becomes more flexible to accept.And the dwindling filter do not make the trial step be denied by current iteration point.Under some reasonable assumptions,the global convergence of the algorithm is proved.Some preliminary numerical experiment results are reported.
Key words:Nonlinear constrained optimization;Line search;Dwindling filter method;Global convergence.
1.Introduction
Nonlinear constrained optimization is one of the most fundamental models in scientific calculation because of the wide use of optimization in science,engineering,economics,industry and so on.[1]The filter method is proposed originally by Fletcher and Leyffer[2]for solving constrained optimization.It has become another popular approach to balance the two competing goals of minimization of the objective function and the satisfaction of the constraints in constrained optimization algorithms.The main idea of filter method and some related convergence results of filter methods are outlined in[3].Filter technique is usually embedded in line search or trust region framework for solving nonlinear constrained optimization.W¨achter and Biegler[4]proposed a filter line search method and prove its global convergence and local convergence.Many variants of line search filter methods are researched.Based on trust-region framework,there are also a lot of research on filter methods(see,e.g.,[5-6]).Recently,Leyffer and Vanaret[1]presented an augmented Lagrangian filter method.
CHEN and SUN[7]proposed a dwindling filter line search method for unconstrained optimization by combining the dwindling multidimensional filter and a second-order line search method.The sequence generated by the algorithm converges to a second-order critical point.GU and ZHU presented dwindling filter methods for nonlinear equality constrained optimization and nonlinear inequality constrained optimization separately in[8]and[9].They also derived a new affine scaling trust region algorithm with dwindling filter for linearly constrained optimization in[10]and developed dwindling filter idea to nest in trust region framework for solving nonlinear optimization in[9].In[10],GU and ZHU presented a three-dimensional dwindling filter algorithm and prove its convergence.Arzani and Peyghami[11]proposed an algorithm equipped with a dwindling multidimensional nonmonotone filter for solving largescale positive definite generalized eigenvalue problems.They also presented a dwindling nonmonotone filter method with derivative-free spectral residual for solving large-scale systems of equations.
In this paper,we focus on nonlinear equality constrained optimization.A different line search dwindling filter method is introduced,which aims to obtain the stationary point of nonlinear equality constrained optimization.The search direction is computed based on the null space method in each iteration.Then,the first-order optimality condition of the nonlinear programming is used as a new filter pair.By adding a dwindling function to the step acceptance criteria,the envelope of the filter becomes thinner and thinner with the decrease of the step size.Then the filter can filter out more unwanted points and reduce the storage of the trial points.Therefore,the calculation cost can be lessened.It is not required to compute the objective function in every iteration.The algorithm only needs to determine the gradient of the objective function and the Hessian of Lagrange function(or an approximation to this Hessian).The proof of global convergence is given.The preliminary numerical results are presented to show the feasibility of the algorithm.
The outline of this paper is as follows.In Section 2,we state the line search filter approach.The global convergence of the algorithm is proved in Section 3.Finally,we report some numerical experiments in Section 4.
The notation of this paper is as follows.Norm‖·‖denotes a fixed vector norm and its compatible matrix norm unless otherwise noted.For brevity,we use the convention(x,y)=(xT,yT)Tfor vectorsx,y.Given two vectorsv,w∈Rn,we define the convex segment[v,w]:={v+t(w-v):t∈[0,1]}.Finally,we denote byO(tk)a sequence{vk}satisfying‖vk‖≤βtkfor some constantβ>0 independent ofk,and byo(tk)a sequence{vk}satisfying‖vk‖≤βktkfor some positive sequence{βk}with=0.
2.A Line Search Filter Approach
Consider the following nonlinear programming(NLP)

where the objective functionf(x):Rn→R and the equality constraintsc(x):Rn→Rmwithm<nare sufficiently smooth.
The Karush-Kuhn-Tucker(KKT)conditions for the NLP(2.1)are

where we denote withA(x):=∇c(x)the transpose of the Jacobian of the constraintsc,and withg(x):=∇f(x)the gradient of the objective function.The vectorycorresponds to the Lagrange multipliers for the equality constraints(2.1b).Under certain constraint qualifications,such as linear independence of the constraint gradients,the KKT conditions are the first order optimality conditions for NLP(2.1).
Given an initial estimatex0,the proposed algorithm of this paper generates a sequence of improved estimatesxkof the solution for the NLP(2.1).In every iterationk,the next iterate point can be determined if the search directionpkand step sizeαkhave worked out,i.e,xk+1:=xk+αkpk,whereαk∈(0,1].
As for the search direction,we have following system(see[12]):

Here,Ak:=A(xk),gk:=g(xk),andck:=c(xk).The symmetric matrixHkdenotes the Hessianof the Lagrangian

of the NLP(2.1),or an approximation to this Hessian.Here,we require that

The vectoryk+1is some estimate of the optimal multipliers corresponding to the equality constrains(2.1b),and its updating formula will be given later(see(2.6)).
Assume that the projection of the Hessian approximationsHkonto the null space ofare uniformly positive definite.Using the methods in[12],pkcan be decompose into

where matricesYk∈Rn×mwhose columns span the range space ofAk,and the columns of matricesNk∈Rn×(n-m)form an orthonormal basis matrix of the null space of.
Substituting(2.5)into(2.3),the following system can be obtained to solvepYandpN:

We can chooseYk=Ak,which is valid forYkwhenhas full row rank.Then a multiplier updating formula as below:

Along this directionpk,the largest step size should be found to satisfy descent condition.Finally,the sequence{xk}of iterates converge to a stationary point of the NLP(2.1).In this paper we consider a backtracking line search procedure to compute the largest step size.A decreasing sequence of step sizesαk,l∈(0,1](l=0,1,2,...)is tried until a certain kind acceptance criterion is satisfied.In the remainder of this section we describe how the filter acceptance criterion can be applied to the line search framework.
According to the first-order optimality condition,the filter pair is defined as(θ(x),ω(x,y)),where

The underlying idea is to interpret the NLP(2.1)as a biobjective optimization problem with two goals:minimizing the constraint violationθ(x)and minimizing the first order criticality measureω(x,y)until they tend to zero.In the filter mechanism,the constraint violation measure is more important,because the optimal solution of NLP problem must be feasible.For both measurements,the trail pointxk(αk,l)can be accepted if it reduces either of the filter pair,i.e.,ifθ(xk(αk,l))<θ(xk)orω(xk(αk,l),yk+1)<ω(xk,yk+1).For convenient,we denoteω(xk)=ω(xk,yk+1).Note that this criterion is not very demanding and therefore generally allows for a larger step size.However,this simple concept is not enough to ensure global convergence.Based on previous experience(see[5]),we have following descent criterion.
A trial step sizeαk,lprovides sufficient reduction with respect to the current iteratexk,if

or
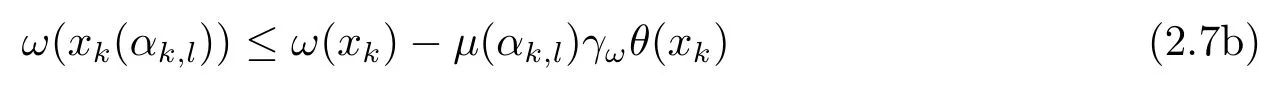
holds for fixed constantsγθ,γω∈(0,1).In a practical implementation,the constantsγθ,γωtypically are chosen to be small.Theμ(α)in this decent criterion is a dwindling function which is the same as the one defined by CHEN and SUN[7]or GU and ZHU[8].
Definition 2.1μ(α):[0,1]→R is a dwindling function if it is a monotonically increasing and continuous function such thatμ(α)=0 if and only ifα=0.
In this paper,we suppose that the dwindling functionμ(α)satisfies

i.e.,μ(α)=o(α).For example,we may chooseμ(α)=α2orμ(α)=.
Sometimes,the descent criterion(2.7)may cause the algorithm to converge to a feasible but not optimal point.In order to prevent it,the following switching conditions should be given:
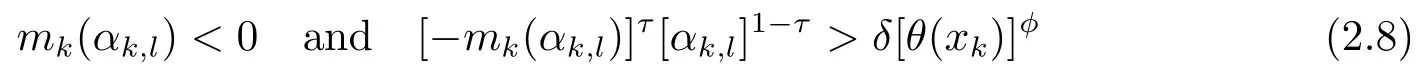
with fixed constantsδ>0,φ>1,τ≥1,where

If the condition(2.8)holds,the steppkis a descent direction.In order to make the current step sizeαk,lacceptable,we require thatαk,lsatisfies the Armijo-type condition

As we have known,the switching condition ensures that for the optimality enforced by the Armijo condition(2.10)is sufficiently large compared to the current constraint violation.Therefore,it prevents a trial point from making only a small progress when it is far away from the feasible region.
For two measuresθandω,a trial point may improve one and worsen the other one.It happens between two such trial points.For preventing this cycle(like methods in[2,4]),a filter is defined as a setFk⊆[0,∞)×R containing all(θ,ω)-pairs that are prohibited in iterationk.We say that a trial pointxk(αk,l)is acceptable to the current filterFkif

During the algorithm we require that the current iteratexkis always acceptable to the current filterFk.After some new iteratesxk+1have been accepted,the current filter can be augmented by
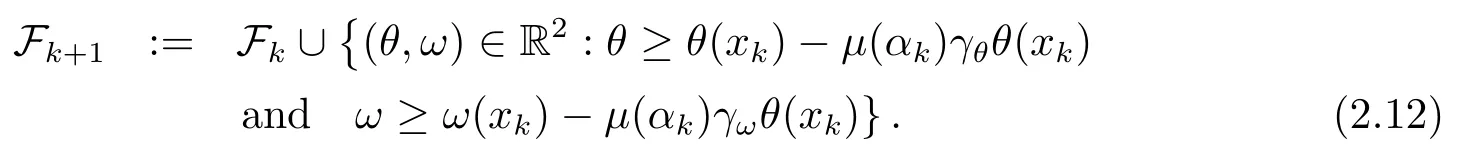
If the filter is not augmented,it remains unchanged,i.e.,Fk+1:=Fk.ThenFk⊆Fk+1holds for allk.
In the algorithm,if a trial pointxk(αk,l)does not satisfy the switching condition(2.8)but satisfies acceptance criterion(2.7),we need use(2.12)to augment filter.If a trial point makes the switching condition(2.8)hold and then makes the Armijo-type condition(2.10)hold,the filter remains unchanged.If the filter has been augmented in iterationk,xkensures to provide sufficient reduction for one of the measures.
The computed trial stepαk,lmay be smaller than
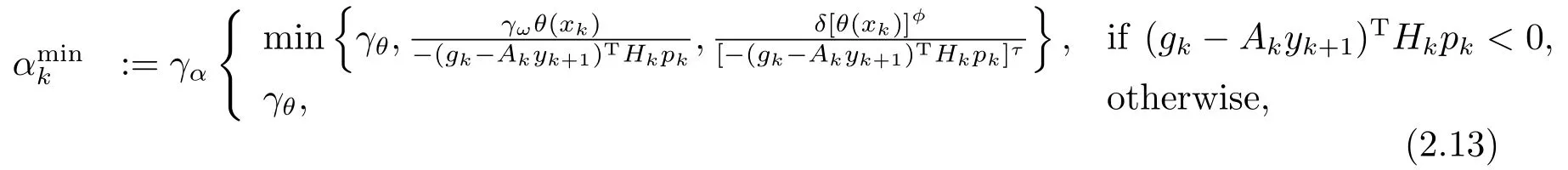
whereγα∈(0,1].Then there is no admissible step size can be found.So the algorithm switches to a feasibility restoration phase,whose purpose is to find a new iteratexk+1that satisfies(2.7)and is also acceptable to the current filter by trying to decrease the constraint violation.Our approach is to compute a new iteratexk+1by decreasing the infeasibility measureθsuch thatxk+1satisfies the sufficient decrease conditions(2.7)and is acceptable to the filter,i.e.,(θ(xk+1),ω(xk+1)).This process can be called the feasibility restoration phase.In(2.13),γαis a safety factor.It is useful to avoid invoking the feasibility restoration phase unnecessarily in a practical implementation.
We are now ready to state the overall algorithm for solving the NLP(2.1)formally.
Algorithm I
Given
Set constantsθmax∈(θ(x0),∞];γθ,γω∈(0,1);δ>0;γα∈(0,1];φ>1;τ≥1;ηω∈.
Initialize
Initialize the starting pointx0,the initial filter
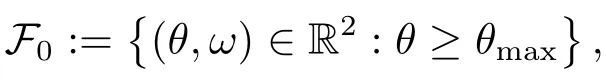
the multipliery0and the iteration counterk=0.
Repeatuntilxksatisfies the KKT conditions(2.2)for someyk+1∈Rm
Compute the search directionpkfrom(2.5);
Compute multiplieryk+1with(2.6).
Setαk,0=1 andl=0.
Repeatuntil findxk(αk,l)is accepted by current filterFk

End repeat
Feasibility restoration phase
Compute a new iteratexk+1.Augment the filter using(2.12)(forxk)and increase the iteration counterk=k+1.Go to the first“Repeat”.
Algorithm I is well defined.In fact,in the second“Repeat”,it is clear that limlαk,l=0.Ifθ(xk)>0,it can be seen from(2.13)that0.So the algorithm either accepts a new iterate or switches to the feasibility restoration phase.On the other hand,ifθ(xk)=0 and the algorithm does not stop at a KKT point,then(gk-Akyk+1)THkpk<0(see Lemma 3.3 below).In that case,=0,and the Armijo condition(2.10)is satisfied,i.e.,a new iterate is accepted.
3.Global Convergence
In the remainder of this paper we denote some index sets.
Z⊆N:the filter is augmented in the corresponding iterations,i.e.,

R⊆Z:the feasibility restoration phase is invoked in the corresponding iterations.
As is common for most line search methods,some reasonable assumptions are stated down below,which is necessary for the global convergence analysis of Algorithm I.
Assumption G
Let{xk}be the sequence generated by Algorithm I.Assume that the feasibility restoration phase always terminates successfully.
(G1)There exists an open setC⊆Rnwith[xk,xk+pk]⊆Cfor allksuch thatfandcare differentiable onC,and their function values,as well as their first derivatives,are bounded and Lipschitz-continuous overC.
(G2)The matricesHkapproximating the Hessian of the Lagrangian in(2.3)are uniformly bounded for allk.
(G3)There exists a constantMH>0 such that

(G4)There exists a constantMA>0 such that

whereσmin(Ak)is the smallest singular value ofAk.
In every iteration,it is possible to make sure that(3.1)is valid by monitoring and possibly modifying the eigenvalues of the reduced Hessian of(2.3)(see[13]).Similarly,we can guarantee that the entire sequence{Hk}is uniformly bounded.
In the convergence analysis of the filter method,we employ

as the criticality measure.Ifθk→0 andχ(xki)→0,then there exists ay*such that the KKT conditions(2.2)are satisfied for(x*,y*).
Let us prove the global convergence of Algorithm I in detail.
Firstly,we give some preliminary results.
Lemma 3.1Suppose Assumption G holds.Then there exist constantsMp,My,Mm>0,such that

for allkandα∈(0,1].
ProofFrom(G1)we have that the right-hand side of(2.3)is uniformly bounded.Additionally,Assumptions(G2),(G3)and(G4)guarantee that the inverse of the matrix in(2.3)exists and is uniformly bounded for allk.Consequently,the solution of(2.3)((pk,yk+1)T)is uniformly bounded,i.e.,‖pk‖≤Mpand‖yk+1‖≤My.From(2.9),we can getmk(α)/α=(gk-Akyk+1)THkpk.So|mk(α)|≤Mmα.
Lemma 3.2Suppose Assumption(G1)holds.Then there exist constantsCθ,Cω>0 such that for allkandα∈(0,1]

ProofThe proof of(3.4a)can be found in Lemma 3.3 from[14].
Next,we give the proof of(3.4b).From the second order Taylor expansions,
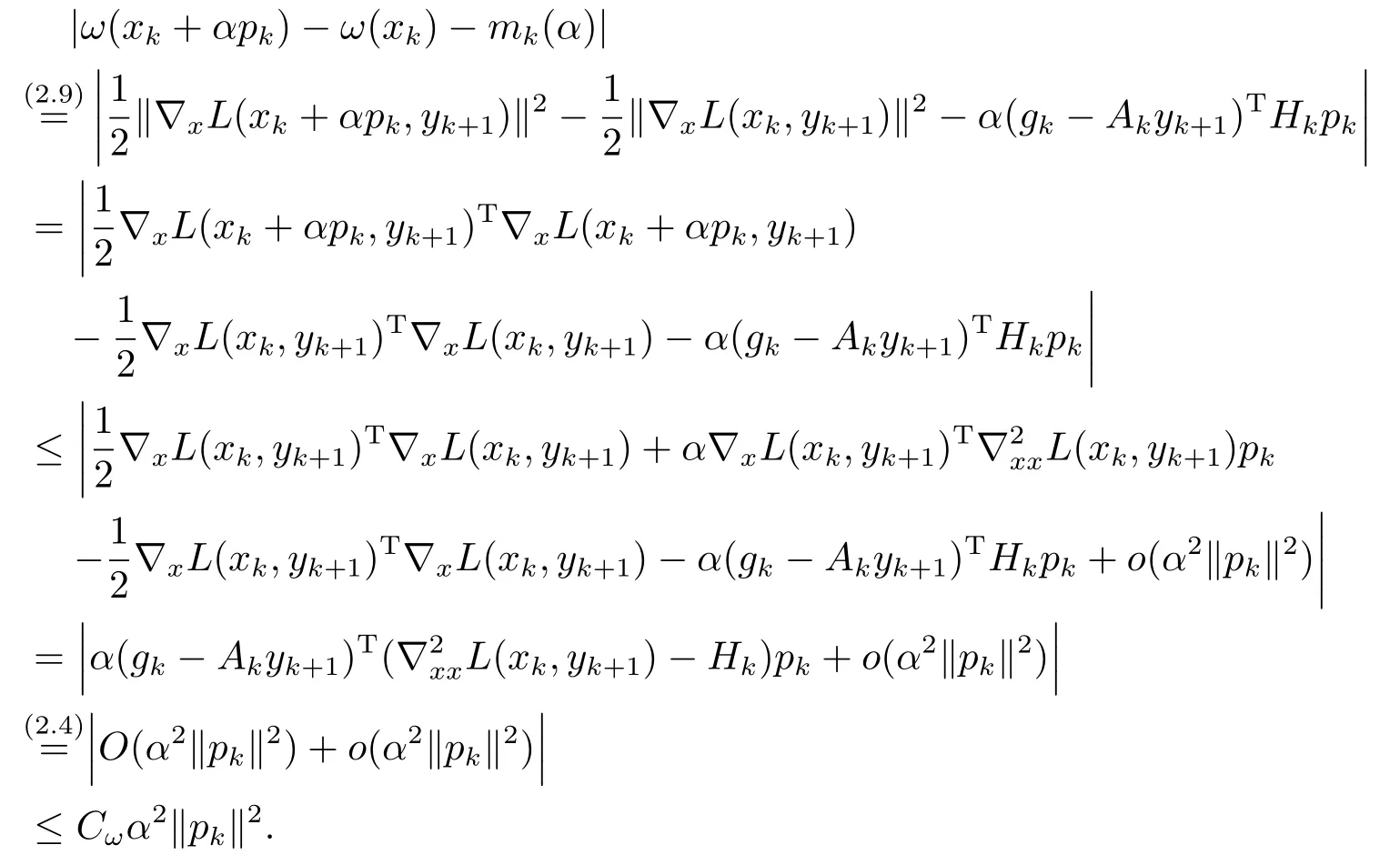
So the conclusion is proved.
Next,we show that feasibility restoration phase of Algorithm I is well defined.Unless the feasibility restoration phase terminates at a stationary point of the constraint violation it is essential that reducing the infeasibility measureθ(x)eventually leads to a point that is acceptable to the filter.This is guaranteed by the following lemma which shows that no(θ,ω)-pair corresponding to a feasible point is ever included in the filter.
Lemma 3.3Suppose Assumption G holds.If{xki}is a subsequence of iterates for whichχ(xki)≥ϵ1with constantsϵ1>0 independent ofi.Then there existsϵ2>0 independent ofi,we have

for alliandα∈(0,1].Then,

for allkandα∈(0,1].
ProofIfθ(xki)=0,butχ(xki)>0,Algorithm I would not terminated.From(2.3)and(3.3),

so

whereϵ2=i.e.,(3.5)holds.
The proof of(3.6)is by induction.From initialize of Algorithm I,it is clear that the statement is valid forki=0 becauseθmax>0.Suppose the statement is true forki.Ifθ(xki)>0 and the filter is augmented in iterationk,it is clear from the update rule(2.12)that Θki+1>0,sinceγθ∈(0,1).On the other hand,ifθ(xki)=0,we have gotmki(α)<0 for allα∈(0,1].So the switching condition(2.8)is true for all trial step sizes.Therefore,algorithm always makesαkihave been accepted then it must have thatαkisatisfies(2.10).Consequently,the filter is not augmented.Hence,Θki+1=Θki>0.
Lemma 3.4Suppose Assumption G holds.Then the trial pointxk(αk,l)could not be rejected byxkifαk,lis sufficiently small.
ProofThere are two cases.
Case 1(θ(xk)>0).Following directly from the second order Taylor expansion ofθ(x),we have

Sinceμ(αk,l)=o(αk,l)asl→0,θ(xk(αk,l))≤θ(xk)-μ(αk,l)γθθ(xk)holds for sufficiently smallαk,l,i.e.,(2.7a)is satisfied.
Case 2(θ(x)=0).From Lemma 3.2 and Lemma 3.3,
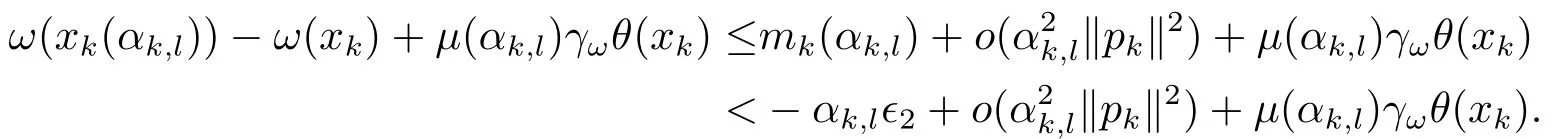
Therefore,ω(xk(αk,l))≤ω(xk)-μ(αk,l)γωθ(xk)holds for sufficiently smallαk,l,i.e.,(2.7b)is satisfied.
Under Assumptions G,the sequenceθ(xk)converges to zero can be proved.That is to say,all limit points of{xk}are feasible(see Lemma 3.5,Lemma 3.6 and Theorem 3.1).Consider from whether the filter is augmented a finite number of times or not.
Lemma 3.5Suppose that Assumption G holds.If the filter is augmented only a finite number of times,i.e.,|Z|<∞.Then

ProofChooseKsuch that for all iterationsk≥Kthe filter is not augmented in iterationk.From the filter augmenting in Algorithm I we then have that for allk≥Kboth conditions(2.8)and(2.10)are satisfied forαk.We now distinguish two cases,where.
Case 1τ>1.From(2.8)it follows withMmfrom Lemma 3.1 that
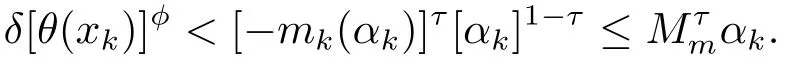
Hence,we can get(αk)τ-1>δτ-1[θ(xk)]φ(τ-1)Mτ(1-τ)mand
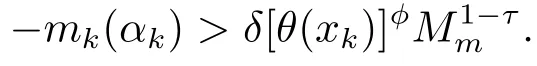
This implies

Case 2τ=1.From(2.8)we haveδ[θ(xk)]φ<-mk(αk)such that from(2.10)we immediately obtain

In either case,we have for allthat


Sinceω(xK+i)is bounded below asi→∞,the series on the right-hand side in the last line is bounded,which in turn implies(3.7).
The following lemma considers a subsequence{xki}withki∈Zfor alli,and its proof is borrowed from the method of[5].
Lemma 3.6Let{xki}be a subsequence of iterates generated by Algorithm I such that the filter is augmented in iterationki,i.e.,ki∈Zfor alli.Furthermore,assume that there exist constantscω∈R andCθ>0 such that
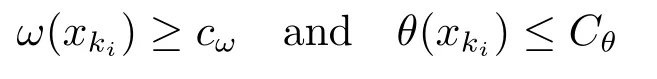
for alli(for example,if Assumption(G1)holds).It then follows that

The previous two lemmas are prepared for the proof of the following theorem.
Theorem 3.1Suppose Assumption G holds.Then

ProofThe proof is similar to Lemma 8 in[15].
The next lemma shows that the Armijo condition(2.10)is satisfied under certain condition that there exists a step length bounded away from zero.
Lemma 3.7Suppose Assumption G holds.Let{xki}be a subsequence.There exists a certain constant>0 such that for allkiandα≤
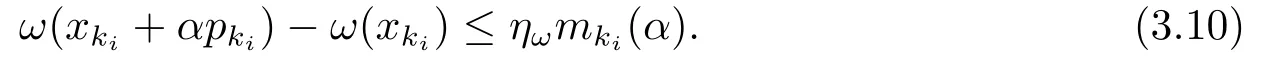
ProofLetMpandCωbe the constants from Lemmas 3.1 and 3.2.It then follows for allwithand from(3.5)that

which implies(3.10).
The previous Theorem 3.1 has proved that a series of points generated by Algorithm I make the constraint violation tend to zero.Next,we prove that Assumption G guarantees that the optimality measureχ(xk)is not bounded away from zero,i.e.,if{xk}is bounded,at least one limit point is a first order optimal point for the NPL(2.1).(see Lemma 3.8 and Theorem 3.2).
Lemma 3.8Suppose that Assumption G holds and that the filter is augmented only a finite number of times,i.e.,|Z|<∞.Then

The proof of Lemma 3.8 is based on Lemma 8 in[4]by using the new filter pair.
In order to find the acceptable step size of the current filter(see(2.11)),we establish a bound of step size as follows.
Lemma 3.9Suppose Assumption G holds.Let{xki}be a subsequence andmki(α)≤-αϵ2for a constantϵ2>0 independent ofkiand for allα∈(0,1].Then there exist constantsc2,c3>0 such that
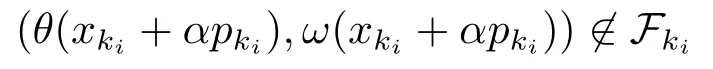
for allkiandα≤min{c2,c3θ(xki)}.
The proof of Lemma 3.9 is similar to Lemma 9 in[4].So,it is omitted.
The last lemma explains that the filter is eventually not augmented when the iteration corresponds to a subsequence with only nonoptimal limit points.This result is used in the proof of the main global convergence theorem to yield a contradiction.
Lemma 3.10Suppose Assumption G holds.Let{xki}be a subsequence of{xk}withχ(xki)≥ϵfor a constantϵ>0 independent ofki.Then there existsK∈N such that for allki≥Kthe filter is not augmented in iterationki,i.e.,kiZ.
Lemma 3.10 can be proved by using the idea of Lemma 10 in[4].
Based on the lemmas and theorem above,we prove the most important conclusion of this paper,that is,the global convergence result of Algorithm I.
Theorem 3.2Suppose Assumption G holds.Then

and

In other words,all limit points are feasible,and if{xk}is bounded,then there exists a limit pointx*of{xk}which is a first order optimal point for the equality constrained NLP(2.1).
Proof(3.11a)follows from Theorem 3.1.In the case of the filter is augmented only a finite number of times,(3.11b)has been proved by Lemma 3.8.Otherwise,there exists a subsequence{xki}such thatki∈Zfor alli.Now suppose that lim supi χ(xki)>0.Then there exist a subsequence{xkij}of{xki}and a constantϵ>0 such that limj θ(xkij)=0 andχ(xkij)>ϵfor allkij.Applying Lemma 3.10 to{xkij},we see that there is an iterationkij,in which the filter is not augmented,i.e.,kijZ.This contradicts the choice of{xki}such that limi χ(xki)=0,which proves(3.11b).
4.Numerical Results
In this section,we report the numerical results of Algorithm I which have been performed on a desktop with Intel(R)Core(TM)i5-8250 CPU.Algorithm I is implemented as a MATLAB code and run under MATLAB version 9.2.0.518641(R2017a).
The selected parameter values are:ϵ=10-6,γθ=10-5,γω=10-5,δ=10-2,γα=10-4,φ=2.01,τ=1.1,ηω=0.25,τ1=0.25;τ2=0.75,The computation terminates when max{‖gk-Akyk+1‖2,‖c(xk)‖}≤ϵis satisfied.The update ofBkis implemented by using the methods recommended in Section 4.4 and Section 4.5 in[16].
The results are reported in Table 4.1 where the test problems are numbered in the same way as in[17]and in[18],respectively.For example,HS49 is the problem 49 in[17]and S335 is the problem 335 in[18].The CPU times in Tab.4.1 are counted in seconds.In these tables,NIT and NG are the numbers of iterations and the numbers of computation of the gradient.In our algorithm,NIT and NG are equal.Furthermore,we compare the numerical experiment results of Algorithm I with the algorithm without dwindling function.To see the results more clearly,we use the logarithmic performance profiles(see Tab.4.2 and Fig.4.1).It can be observed that Algorithm I with dwindling function performs better than that without dwindling function.

Fig.4.1 The comparison of Algorithm and the algorithm without dwindling function

Tab.4.1 Numerical results of Algorithm I
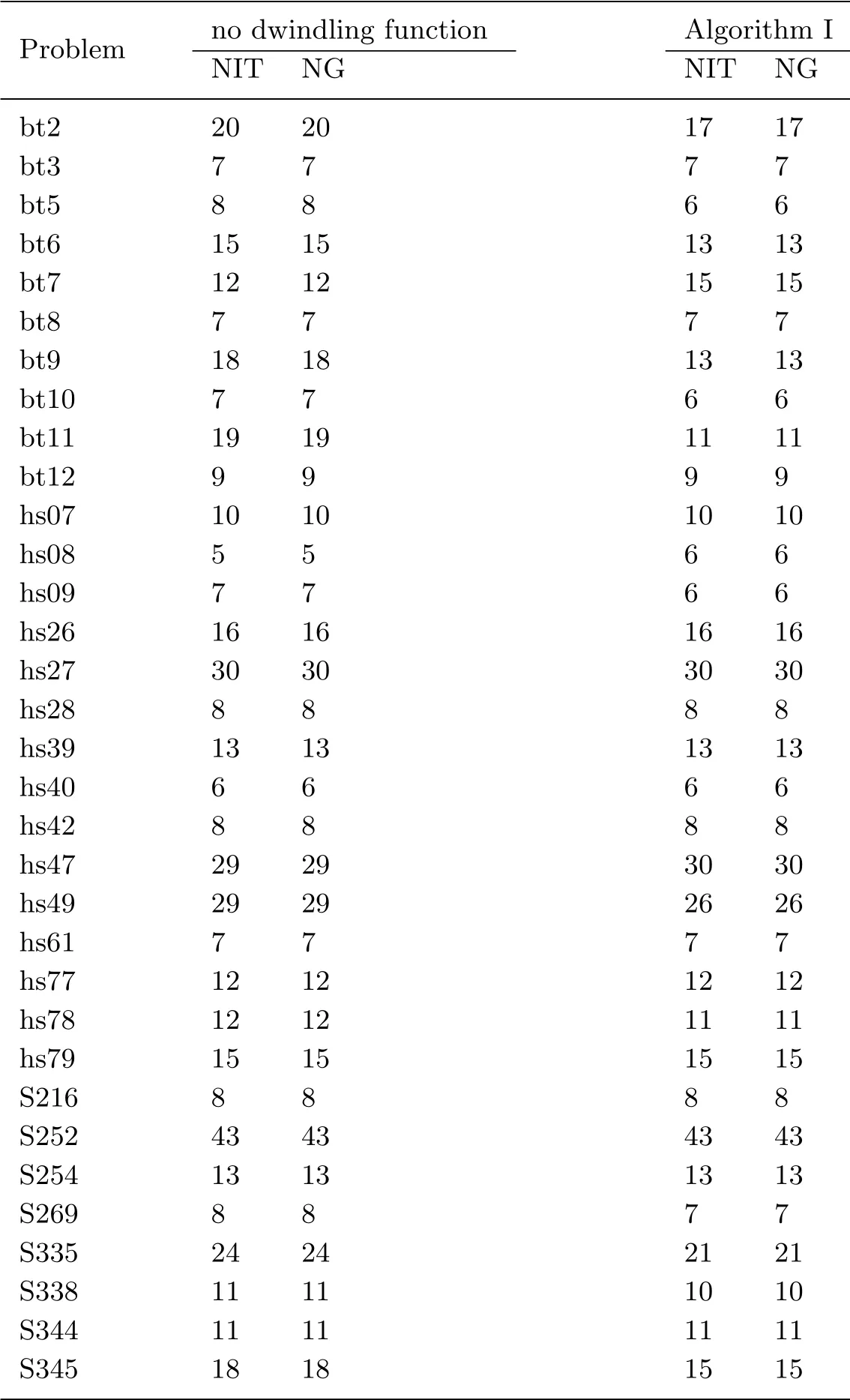
Tab.4.2 The comparison of whether there exists a dwindling function
5.Conclusion
We have introduced a dwindling filter line search method for solving nonlinear equality constrained optimization.The global convergence analysis for this algorithm is presented under some reasonable assumptions.The preliminary numerical experiments show its practical performance.The comparison of numerical experiment data shows that the algorithm in this paper has good effect.However,the analysis of local convergence rate is absent.That is what we are working on.

