一类具有病毒变异的随机SEIR传染病模型的灭绝性与平稳分布
杜金姬,秦闯亮,陈海波,李秋英
(1.信阳学院数学与统计学院,河南信阳464000;2.中南大学数学与统计学院,湖南长沙410075;3.黄淮学院数学与统计学院,河南驻马店463000)
1.引言
人们一直在使用动力学方法来研究传染病的传播,并预测每次抵达流行病的趋势[1-5].如果在传染病的传播过程中出现突变,很容易导致疾病失控.例如禽流感病毒(H7N9)、乙型肝炎及其他疾病.因此,研究遗传变异病毒的过程有助于了解疾病和控制疾病的传播.最近,文[6]中研究了一类具有病毒变异的SEIR传染病模型的动力学行为.另外,实际生活中任何事物都受到环境波动的影响.因此,研究环境噪音对于疾病的影响是十分必要的[7-9].本文在文[6]模型的基础上加入随机扰动,提出随机SEIR传染病模型:

模型(1.1)中,总人口N被分成了五部分S,E,I1,I2,R且N=S+E+I1+I2+R.S,E,I1,I2,R分别表示t时刻易感者,潜伏者,病毒变异前的感染者,病毒变异后的感染者,康复者,μ为总人口出生率,d表示自然死亡率,β1为病毒变异前感染个体的感染率,β2为病毒变异后感染个体的感染率,K表示环境容纳量,δ为病毒变异前的感染者变成病毒变异后的感染者的比率,α表示是病毒变异前潜伏个体成为感染个体的系数,k1为病毒变异前感染者的恢复率,k2为病毒变异后感染者恢复率.参数μ,d,K,β1,β2是正常数,δ,α,k1,k2为非负常数.Bi(t)(i=1,2,3,4,5)是定义在一个完备概率空间(Ω,F,{F}t≥0,P)上的标准布朗运动,{F}t≥0满足非降和右连续,0(i=1,2,3,4,5)表示白噪音强度.
在模型(1.1)中,总人口N(t)满足


注意到变量s,e,i1,i2,r满足关系r=1-s-e-i1-i2,我们可以忽略模型(1.2)的第五个方程探索简化模型

其中初始值(s(0),e(0),i1(0),i2(0))∈且s(0)+e(0)+i1(0)+i2(0)<1.
2.全局正解的存在唯一性
为了研究系统(1.3)的动力学行为,我们首先证明系统存在全局正解.
定理2.1对于任意的初值(s(0),e(0),i1(0),i2(0))∈且s(0)+e(0)+i1(0)+i2(0)<1,当t>0时,模型(1.3)存在唯一正解(s(t),e(t),i1(t),i2(t))并且以概率1位于内.
证因为模型(1.3)的系数满足局部Lipschitz条件,则对任意初值(s(0),e(0),i1(0),i2(0))∈,存在一个t∈[0,τe)上的唯一局部正解(s(t),e(t),i1(t),i2(t))∈,其中τe为停时.为了证明解是全局的,我们仅需证明τe=∞a.s.为此,设k0>0充分大,使s(0),e(0),i1(0),i2(0)位于区间内.对每个整数k≥k0,定义停时

记inf∅=∞(∅表示空集).明显地,τk随着k→∞不断增加.令因此τ∞≤τea.s.如果能证明τ∞=∞a.s.则τe=∞a.s.并且对所有的t≥0,(s(t),e(t),i1(t),i2(t))∈a.s.也就是需要证明τ∞=∞a.s.如果不成立,那么存在一对常数T>0和ε∈(0,1)使得P{τ∞≤T}≥ε.因此,存在一个数k1≥k0使得对所有的k≥k1,成立

定义一个C2-函数V:→R+如下:


其中

因为r=1-s-e-i1-i2,所以
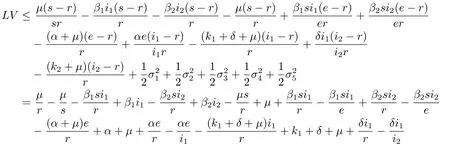

因此我们有
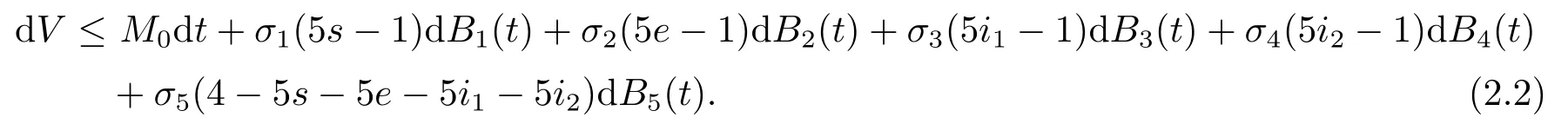
对(2.2)两边从0到τk∧T积分并取期望得

令Ωk={τk≤T},k≥k1及由(2.1)式,有P(Ωk)≥ε.注意到对任意ω∈Ωk,都存在s(τk,ω),e(τk,ω),i1(τk,ω),i2(τk,ω)等于或k.因此

由(2.3)和(2.4)式,我们有

其中1Ωk(ω)是Ωk(ω)的特征函数.
令k→∞,则有

矛盾.显然有τ∞=∞.定理得证.
3.疾病的灭绝性
本节我们讨论系统(1.3)中疾病的灭绝性.
定理3.1对任意的初值(s(0),e(0),i1(0),i2(0))∈且s(0)+e(0)+i1(0)+i2(0)<1,若条件

同时成立,则(e(t),i1(t),i2(t))指数收敛于(0,0,0)a.s.即疾病灭绝,其中

及
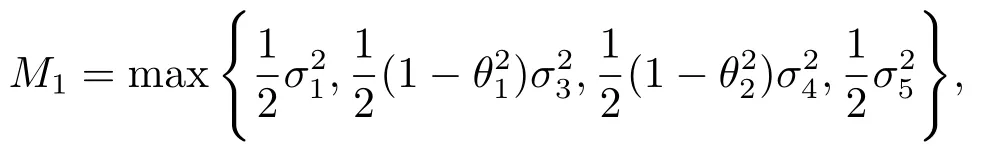

证定义一个可微函数V:

其中θ1,θ2是待定正数.根据公式及模型(1.3),得

其中
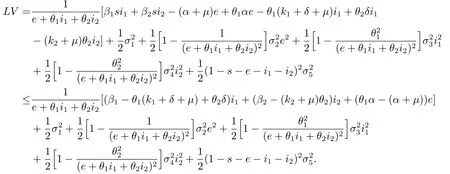
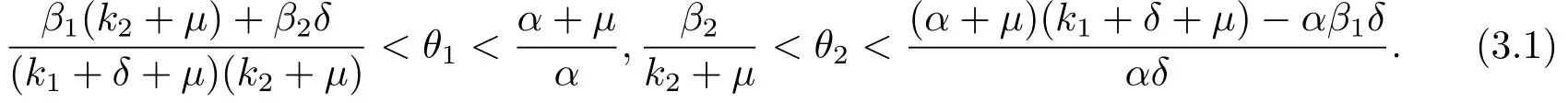
由(3.1)式,存在正数m使得
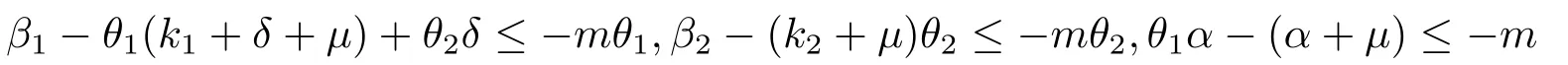
同时成立.因此有m<k1+δ+μ,且及m<α+μ,且及m<k2+μ,且≤-m+k2+μ同时成立,则可取

因此有


其中

由强大数定律得
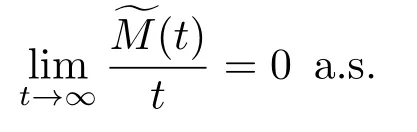
因此,

即

证毕.
4.平稳分布及遍历性
本节基于Khasminskii理论和Lyapunov函数法研究模型存在遍历平稳分布的条件,首先给出所需引理.
令X(t)是定义在d维Euclidean空间Ed上的齐Markov过程,并可有如下的随机微分方程来描述:

对应的扩散矩阵为
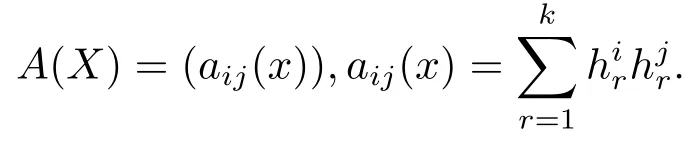
引理4.1[10]如果存在一个有规则边界Γ的有界域D⊂Ed,并且:
(i)存在一个正数M,使得
(ii)存在一个非负C2函数V,使得LV对任意的x∈EdD是负的.则Markov过程X(t)存在唯一的遍历平稳分布π(·).
定理4.1设是系统(1.3)满足初始条件及s(0)+e(0)+i1(0)+i2(0)<1的解.若条件
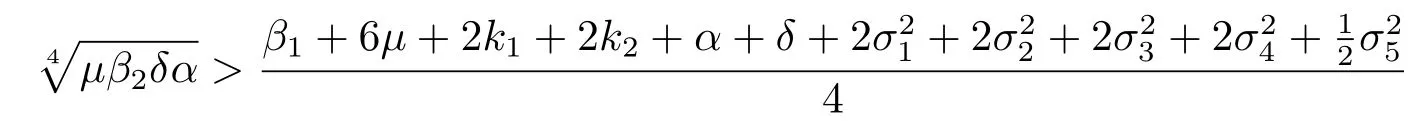
成立,则系统(1.3)存在唯一的遍历平稳分布π(·).
证定义正定函数V
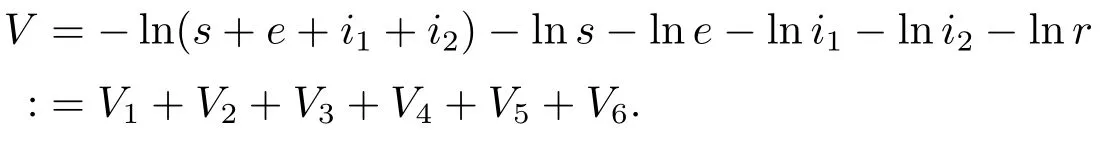

类似地,

因此,

其中
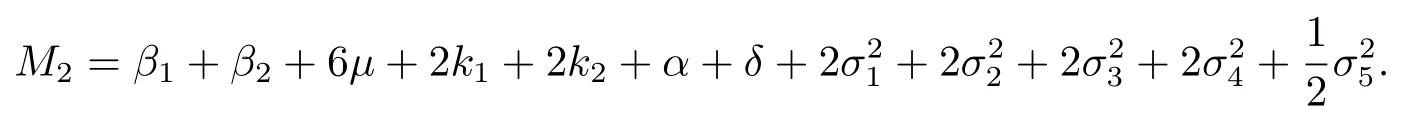
定义紧子集D:

其中

且ψi∈(0,1)足够小满足下列条件:


那么

其中

下面我们证明LV恒负.
情况1 如果(s,e,i1,i2)∈D1,由(4.1)及(4.3)得

情况2 如果(s,e,i1,i2)∈D2,由(4.1)、(4.2)及(4.4)得
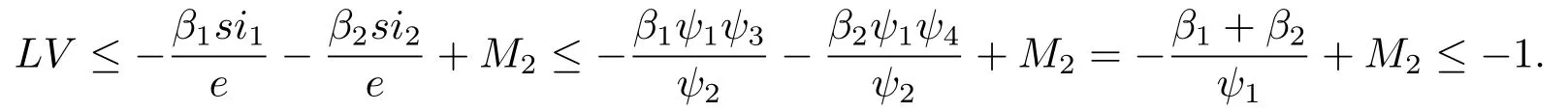
情况3 如果(s,e,i1,i2)∈D3,由(4.1)及(4.5)得
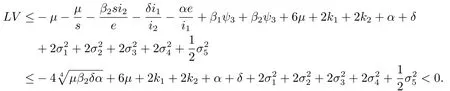
情况4 如果(s,e,i1,i2)∈D4,由(4.1)及(4.6)得
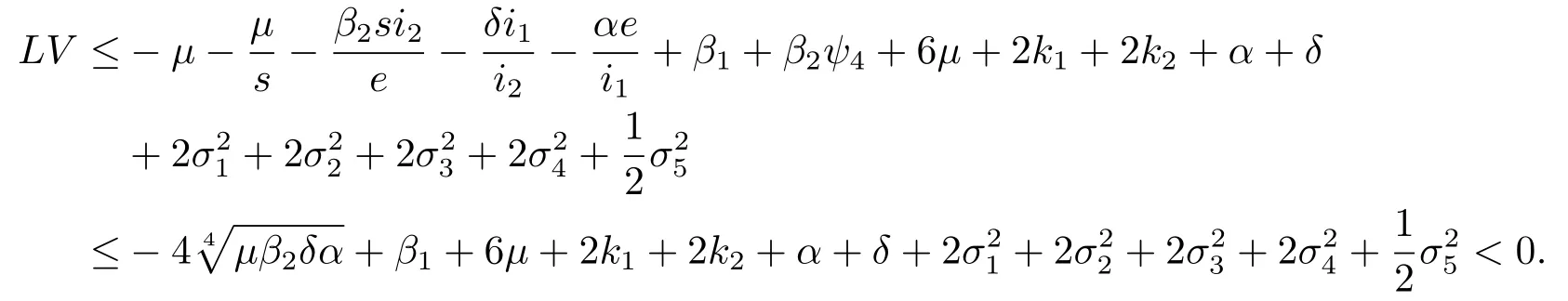
情况5 如果(s,e,i1,i2)∈D5,由(4.1)及(4.7)得

情况6 如果(s,e,i1,i2)∈D6,由(4.1)及(4.8)得

定义

显然对任意(s,e,i1,i2)∈D,有LV≤ζ<0.另外,存在正数
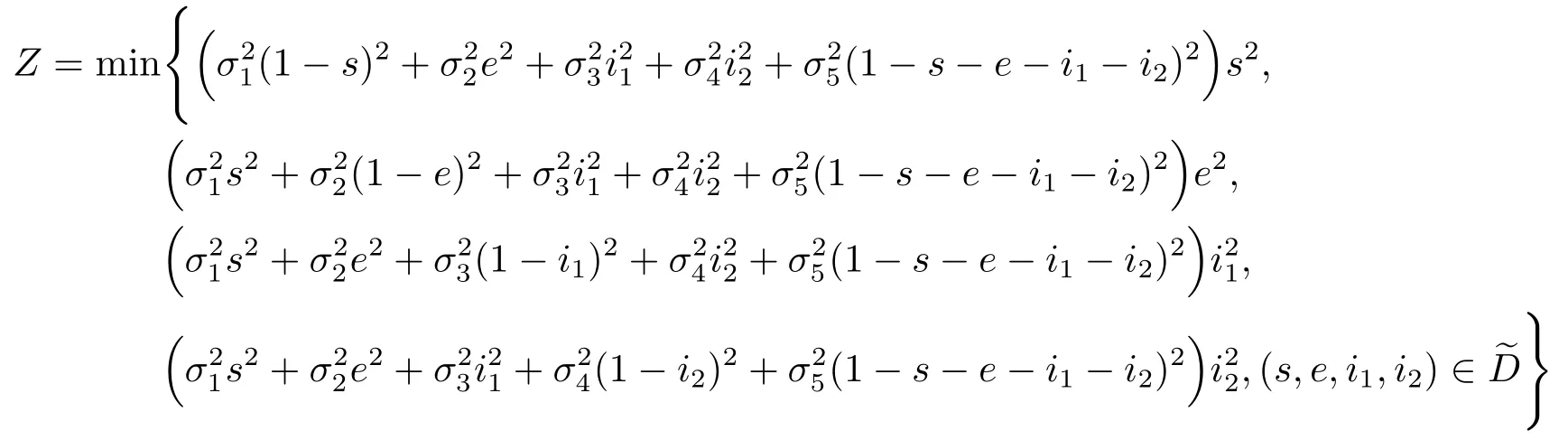
使得

由引理4.1知,定理4.1结论成立.
5.数值模拟和结论
本节中我们通过数值模拟说明结果的正确性.
图5.1中取s(0)=0.35,e(0)=0.25,i1(0)=0.15,i2(0)=0.1,μ=0.1,β1=0.0005,β2=0.0016,k1=0.0666,k2=0.1428,δ=0.05,α=0.04,σ1=0.31,σ2=0.2,σ3=0.22,σ4=σ5=0.2,则M1=0.04805<m≈0.2424,满足定理3.1的条件,由定理的结论可知疾病将灭绝.
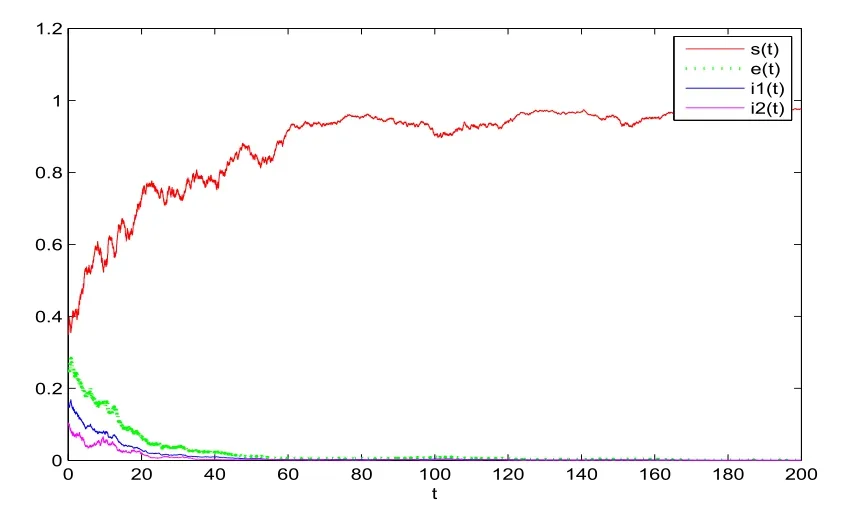
图5.1 受感染个体灭绝的时间时序图
图5.2中取s(0)=0.45,e(0)=0.2,i1(0)=0.15,i2(0)=0.1,μ=0.01,β1=0.06,β2=1,k1=0.0222,k2=0.01428,δ=0.1,α=0.1,σ1=σ2=σ3=σ4=σ5=0.02,则满足定理4.1的条件,则系统存在唯一的遍历平稳分布.

图5.2 模型(1.3)的解s(t),e(t),i1(t),i1(t)及其密度函数图
本文应用随机分析的方法研究了一类高维随机简化比例传染病模型,得到疾病灭绝和系统正解存在唯一遍历平稳分布的充分条件,对模型的研究更加有利于控制疾病的传播.

