b-距离空间中隐性压缩不动点定理

2021-06-30 00:09王宏颖贺飞

应用数学 2021年3期

王宏颖，贺飞

(内蒙古大学数学科学学院，内蒙古呼和浩特010021)

1.引言

1993年，Czerwik[1]引入了b-距离空间的概念.当空间系数s=1时，该类空间为距离空间，因此b-距离空间是距离空间的推广.此后许多学者将各种形式的不动点定理建立到b-距离空间中，例如见文[2-4].另一方面，2011年，Berinde等人[5]在距离空间中建立了含有六元连续函数的隐性压缩不动点定理.之后，有些学者在距离空间讨论并发展含有六元函数的压缩不动点定理的其他形式，例如见文[6-10].最近，Karapinar等人[11]和Aydi等人[12]定义了一类新的函数，并分别在距离空间，四角距离空间下建立了几类隐性压缩的不动点定理.

本文在b-距离空间中建立了两类含有六元连续函数的隐性压缩不动点定理.第一个结果将Berinde等人[5]的隐性压缩不动点定理推广到b-距离空间.应用我们的结果可以推出b-距离空间的Banach型，Chatterjea型，Kannan型压缩不动点定理.2015年，Dung等人[13]成功解决了Jovanovi等人[14]提出的公开问题，即将b-距离空间中经典Banach压缩不动点定理的压缩系数从放宽为[0，1).我们的结果也可以推出Dung等人的结果.第二个结果将距离空间中Karapinar等人[11]提出的新的Kannan型压缩不动点定理和四角距离空间中Aydi等人[12]提出的新的´Ciri´c-Reich-Rus型压缩不动点定理建立到b-距离空间，并统一了这两种类型的压缩条件.

2.预备知识与主要结果

首先我们来回顾一下b-距离空间一些基本定义和性质.

定义2.1[1]设X是一个非空集合，s≥1是给定的正实数，如果函数d:X×X→[0，∞)满足以下条件:

(b1)d(x，y)=0，当且仅当x=y;

(b2)d(x，y)=d(y，x);

(b3)d(x，y)≤s[d(x，z)+d(z，y)]，

则称d为X的b-距离，且称(X，d)为b-距离空间，其中s称为(X，d)的系数.

显然，b-距离空间是距离空间的推广.

定义2.2[1]设(X，d)是系数为s≥1的b-距离空间，{xn}是X中的点列.

1)点列{xn}收敛于x∈X，当且仅当

2)点列{xn}是Cauchy列，当且仅当

3)空间(X，d)是完备，当且仅当X中的任意Cauchy列都收敛.

下面是Suzuki[15]提出的b-距离空间中的一个重要引理.进一步，此引理可以被推广到类拟b-距离空间中，参见文[16].

引理2.1[15]设(X，d)是系数s≥1的b-距离空间，{xn}⊂X.如果存在一个r∈[0，1)，使得对任意n∈N，满足

那么{xn}是一个Cauchy列.

下面介绍含有六元函数的隐性压缩的相关概念.

设F是满足以下两个条件的六元实值连续函数F:→R+的集合，

(F1)F关于第五变元是非增的，且对任意s≥1，存在h∈[0，1)，满足

(F2)对任意的u＞0，有F(u，u，0，0，u，u)＞0.

我们给出一些满足隐性关系的六元连续函数F的具体例子.

其中取h=max(s≥1);

5)设a∈[0，1)，且

6)设a∈[0，

其中取h=(s≥1).

下面例子说明隐性压缩条件中的(F1)和(F2)是相互独立的.

本计划第二天清晨永远离开秦川，可是现在，艾莉突然想在这里多住几天。很显然女人不过将她当成一个试图混进豪宅的女孩——煮咖啡，煮牛奶，洗刷餐具，洗刷马桶，拿不菲的薪水，住豪华的房子……然后，趁女主人不注意，与男主人调情或者偷情——艾莉相信这样的生活对很多年轻并且贫困的女孩极具吸引力。现在她必须让女人相信她是秦川买来的充气娃娃——工厂出来的产品，供男人发泄性欲的玩具。她对他们的生活不会造成丝毫影响。

例2.2令a∈[0，1)，L≥0.

1)设F(t1，t2，t3，t4，t5，t6)=t1-at2-Lt6.容易证明F满足(F1)，其中取h=a，但当L＞1时，F不满足(F2);

2)设F(t1，t2，t3，t4，t5，t6)=t1-at2-Lt3.容易证明F满足(F2)，但当L＞1时，F不满足(F1).

例2.3设F:R6+→R+，容易验证下列定义的F同时满足(F1)和(F2).

1)设λ∈[0，1)，α∈(0，1)，F(t1，t2，t3，t4，t5，t6)=t1-其中取h=

2)设a∈[0，1)，α，β＞0，α+β＜1，

下面给出本文第一个主要结果.

定理2.1设(X，d)是系数为s的完备b-距离空间.设T是X→X的自映射，且满足存在F∈F，使得对任意x，y∈X，有

如果d连续或者T连续，那么

(a)T在X中有唯一不动点x*;

(b)由xn+1=Txn，n=0，1，···定义的迭代点列收敛于x*;

(c)当sh＜1时，有以下估计成立

证任取x0∈X，令xn+1=Txn=Tnx0，n=0，1，2，···，由此构造迭代点列{xn}.

第1步证明{xn}是Cauchy列.

由(2.1)式可得

即

由b-距离空间的三角不等式可得

由于F满足条件(F1)且关于第五变元是非增的，故

由F满足条件(F1)可知，存在h∈[0，1)，使得

由(2.2)和引理2.1可得，{xn}是X中Cauchy列.又由于X是完备的，故存在x*∈X，使得

此时结论(b)得证.

第2步证明x*为T的不动点.

以下分d连续和T连续两种情况证明.

情况1若d有连续性.

由(2.1)可得

即

对(2.4)两边同时取极限，由F和d的连续性可得

由于F关于第五变元是非增的，故

由上式和F满足条件(F1)可知，存在h∈[0，1)，使得d(x*，Tx*)≤h0=0，即x*=Tx*.

情况2若T是连续的.

由(2.3)和T的连续性可得

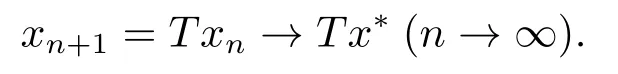
由于极限的唯一性，故x*=Tx*.

第3步证明不动点的唯一性.

反证法，假设T存在另一个不动点y*且x*y*，则d(x*，y*)＞0.由(2.1)可得

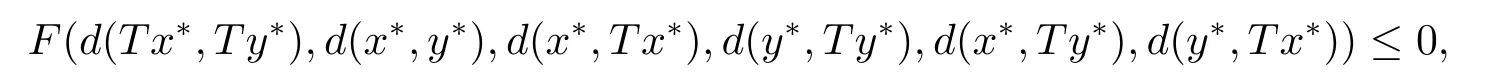
即

与F满足条件(F2)矛盾.因此T有唯一的不动点x*.

下证结论(c)成立.

由(2.2)可得

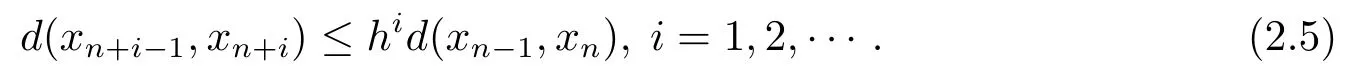
由(2.5)及三角不等式可得

令p→∞时，可得结论(c)成立.

评注2.1当s=1时，定理2.1为Berinde[5]在距离空间下建立的含有六元函数的隐性压缩不动点定理(文[5]中定理3.3)，因此是Berinde结果的推广.

2018年，Karapinar等人[11]在距离空间中给出了另一类新的压缩形式的定义，并证明了相关隐性压缩不动点定理.2019年，Aydi等人[12]在四角距离空间下建立了该类隐性压缩不动点定理.之后许多学者在不同空间下建立该类型的隐性压缩不动点定理.下面我们将Karapinar等人和Aydi等人的结果建立到b-距离空间.

定理2.2设(X，d)是系数为s的完备b-距离空间，T是X→X的自映射满足，存在六元实值连续函数F:R+满足条件(F1)，使得对任意x，y∈XFix{T}，有若d连续或者T连续时，则