关于部分变元强稳定性的几个定理
刘丹
(山东科技大学数学与系统科学学院,山东青岛266590)
关于部分变元强稳定性的几个定理
刘丹
(山东科技大学数学与系统科学学院,山东青岛266590)
本文给出了微分系统关于部分变元的强渐进稳定及在持续摄动下强渐进稳定的几个定理,改进和推广了已有文献的相关结果.
部分变元;强渐近稳定;持续摄动;强一致稳定
1 引言
众所周知,Liapunov直接法是研究系统稳定性的一个十分有效的方法.目前,围绕Liapunov意义下的稳定性、部分变元的稳定性的结果比较丰富,如文献[1-5].然而近几十年来,人们根据实际情况的需求提出了关于部分变元的强稳定性的概念.运用Liapunov直接法研究部分变元的强稳定性的成果还不够丰富.本文将借鉴文献[6-9]的基本思想,讨论部分变元的强渐进稳定、强一致渐进稳定,并推广到有扰动项的持续摄动下关于部分变元的强一致稳定和强渐进稳定.
2 定义与引理
考虑n维非自治系统

其中x∈Rn,f(t,x)∈C[I×Ω,Rn],I=[0,+∞),Ω为开区域,f(t,0)≡0.记
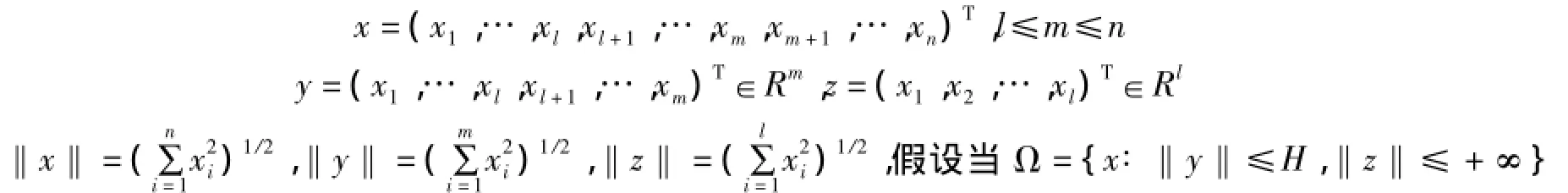
时,(1)的解唯一且可延拓到I上.
对于(1)式的扰动系统

其中R(t,x)∈C[I×Ω,Rn],R(t,0)=0,R(t,0)不恒为零.
定义1[1]称(1)的平凡解关于部分变元z对y强稳定,如果对于任何ε>0和t0∈I,存在δ(ε,t0)>0,使得当x0满足‖y0‖≤δ(ε)时,对一切t≥t0,有‖z(t,t0,x0)‖≤ε.
定义2[1]称(1)的平凡解关于部分变元z对y强一致稳定,如果对于任何ε>0,存在δ(ε)>0,使得当x0满足‖y0‖≤δ(ε,t0)时,对一切t0∈I,当t≥t0时有‖z(t,t0,x0)‖≤ε.
定义3[1]称(1)的平凡解关于部分变元z对y强吸引的,如果对于任意ε>0及t0∈I,存在δ(t0)>0,使得当x0满足‖y0‖≤δ时,存在T(ε,t0,x0)>0,当t≥t0+T(ε,t0,x0)时有‖z(t,t0,x0)‖<ε,即
定义4[2]称(1)的平凡解关于部分变元z对y强渐近稳定的,若(1)的平凡解关于部分变元z对y是强稳定的且z对y是强吸引的.
定义5[1]称(1)的平凡解关于部分变元z对y强等度渐近稳定的,若(1)的平凡解关于部分变元z对y是强稳定,且对任意ε>0及t0∈I,存在δ(t0)>0及T(ε,t0)>0,使得当x0满足‖y0‖≤δ时,对t≥t0+T(ε,t0)时有‖z(t,t0,x0)‖<ε.
定义6[1]称(1)的平凡解关于部分变元z对y强一致渐近稳定的,若(1)的平凡解关于部分变元z对y是强一致稳定,且δ>0,对任意ε>0及t0∈I,存在T(ε,δ)>0,使得当x0满足‖y0‖≤δ时,对t≥t0+T(ε,δ)时有‖z(t,t0,x0)‖<ε.
定义7[1]对于连续函数V(t,x)=V(t,y,z),若有V(t,0,z)≡0,则称V(t,x)为推广的Liapunov函数或y-V函数.
定义8称式(1)的平凡解在每时刻很小的经干扰下关于部分变元z对y强一致稳定,若对且任意的ε>0及t0∈I,存在δ1(ε)>0和δ2(ε)>0,使满足当‖y0‖<δ1(ε)与‖R(t,x)‖<δ2(ε)时,对t≥t0,有‖z(t,t0,x0)‖<ε.
定义9称式(1)的平凡解在每时刻很小的经干扰下关于部分变元z对y强吸引,若对且任意的ε>0及t0∈I,存在δ(t0)>0和T(ε)>0,使满足当‖y0‖<δ(t0),对t≥t0+T,有‖z(t,t0,x0)‖<ε.
引理[1]若存在y-V函数V(t,x)满足:(1)φ(‖z‖)≤V(t,x)φ∈K;(2)D+V|(1)≤0),称式(1)的平凡解关于部分变元z对y是强稳定的.
3 主要结果
定理1存在y-V函数V(t,x)满足:
(1)φ1(‖z‖)≤V(t,x),φ1∈K,
(2)D+V|(1)≤-g(t)φ2(‖y‖),φ2∈K,其中g(t)≥0且
则系统(1)平凡解关于部分变元z对y强渐近稳定.
证明由引理可知,式(1)的平凡解关于部分变元z对y是强稳定的.下面证明(1)平凡解关于部分变元z对y是强吸引的,即有∀ε>0,存在δ(t0)>0,使得当‖y0‖≤δ(ε,t0)时,有y0,z0))=V∞>0.
从而φ1(‖z‖)≤V(t,x(t,t0,y0,z0))→0(t→+∞),‖z‖→0(t→+∞).
若不然,则存在t0∈I,∀δ>0,当‖y0‖≤δ时,有
由条件(2)可知D+V|(1)<0,故有tlim+V(t,x(t,t0,y0,z0))△=V∞.
→∞
从而V(t,x(t,t0,y0,z0))≥V∞>0,利用条件(1)和(2)可知,D+V|(1)≤-g(t)φ3(φ-12(V∞)).
故可得到0≤V(t,x(t,t0,y0,z0))≤V(t0,y0,z0)-φ3(δ(ε))
而当t≫t0时上式不成立.于是
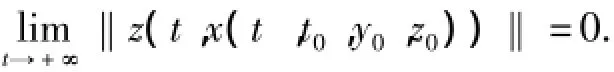
证得系统(1)平凡解关于部分变元z对y强渐近稳定.
定理2存在y-V函数V(t,x)满足:
(1)φ1(‖z‖)≤V(t,x)≤φ2(‖y‖),φi∈K(i=1,2,3),
(2)D+V|(1)≤-g(t)φ3(‖y‖),其中g(t)≥0且对于∀B>0都存在b>0使得系统(1)平凡解关于部分变元z对y强一致渐近稳定.
证明先证明系统(1)平凡解关于部分变元z对y强一致稳定性.
对∀ε>0,取δ(ε)=φ-12(φ1(ε)),当‖y0‖<δ(ε)时,由已知条件有
φ1(‖z(t,t0,x0)‖)≤V(t,x(t,t0,y0,z0))≤V(t0,y0,z0)≤φ2(‖y(t,t0,x0)‖)<φ1(ε),即‖z(t,t0,x0)‖<ε.
下证系统(1)强一致吸引性,对∀ε>0,存在△0>0,使得当‖y0‖≤△0时,∃T(ε)>0,当t≥t0+ T(ε)时,有‖z(t,t0,x0)‖≤ε.
设对于△0=δ(H),当‖y0‖≤△0,取有已知条件(2),存在T>0,当任意t0∈I有则一定存在t1∈[t0,t0+T],使‖y0(t1,t0,y0,z0)‖≤δ(ε).
若不然,∀t∈[t0,t0+T]有‖y0(t1,t0,y0,z0)‖≥δ(ε),由已知条件(2)有D+V|(1)≤-g(t)φ3(δ (ε)),即
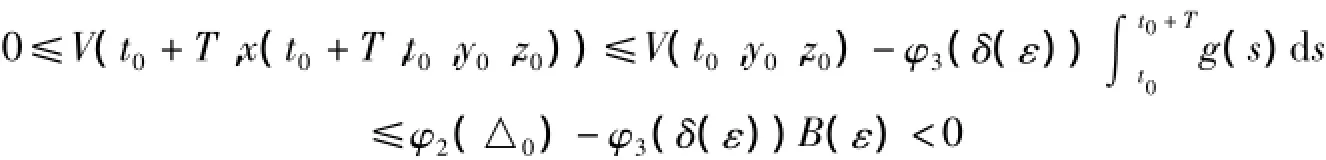
这与V(t,x)正定矛盾.
因此,存在t1∈[t0,t0+T]使‖y0(t1,t0,y0,z0)‖≥δ(ε),从而有

即当t≥t0+T时,有‖z(t,t0,x0)‖≤ε.证得系统(1)平凡解关于部分变元z对y强一致吸引.
综上可得,系统(1)平凡解关于部分变元z对y强一致渐近稳定性.
推论1存在y-V函数V(t,x)满足:
(1)φ1(‖z‖)≤V(t,x)≤φ2(‖y‖),φi∈K(i=1,2,3),
(2)D+V|(1)≤-g(t)φ3(‖y‖),其中g(t)≥0且
则系统(1)平凡解关于部分变元z对y强等度渐近稳定.
证明由条件(1)和(2)可表示为D+V|(1)≤-g(t)φ3(φ-12(V(t,x)))
证明过程与定理2的方法类似,此定理显然是成立的.
定理3存在y-V函数V(t,x)满足:
(2)φ1(‖z‖)≤V(t,x)≤φ2(‖y‖),φi∈K(i=1,2,3);
(3)D+V|(1)≤-g(t)φ3(‖y‖).
则有式(1)平凡解在每时刻很小的经干扰下关于部分变元z对y强一致稳定.
证明由条件(2)有‖y‖≥φ-12(V(t,x)).由条件(3)

即‖z(t,t0,x0)‖<ε.
对∀ε>0,‖R(t,x)‖<δ2(ε)时,由条件(3)知D+V|(1)<0.当‖y0‖<δ1(ε)时,有V(t0,y0,z0)≤φ1(‖ε‖).
需证t≥t0,V(t,x(t,t0,y0,z0))<φ1(‖ε‖).
若不然,则存在t1∈I使V(t1,x(t1,t0,y0,z0))=φ1(‖ε‖),于是∃t'0∈(t0,t1)使
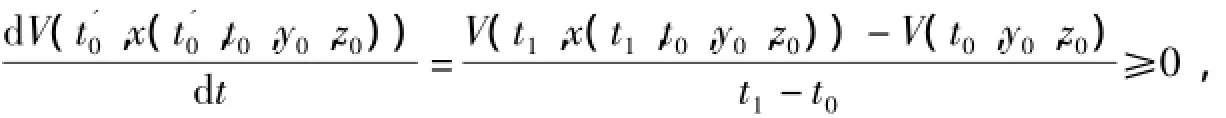
这与D+V|(1)<0矛盾.从而有φ1(‖z(t,t0,x0)‖)≤V(t,x(t,t0,y0,z0))≤φ1(‖ε‖).
即‖z(t,t0,x0)‖<ε(t≥t0),式(1)平凡解在每时刻很小的经干扰下关于部分变元z对y强一致稳定.
证明对定理3中的条件(2)的解有
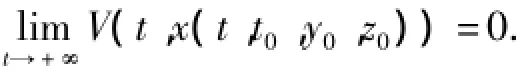
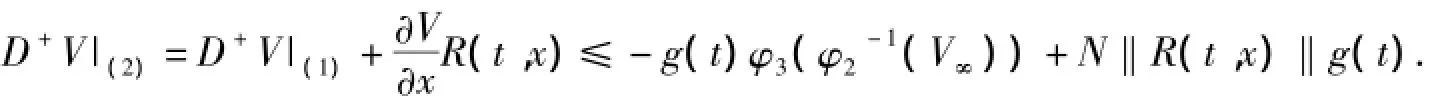
取T1>T,当t≥t0+T1时有‖R(t,x)‖≤r≤φ3(φ2-1(V∞))/N.
因此D+V|(2)≤-g(t)φ3(φ2-1(V∞))+Nrg(t).
[1]廖晓昕.稳定性的数学理论与应用[M].武汉:华中师范大学出版社,1988.
[2]蹇继贵,万新敏.关于微分方程部分变远渐近稳定性定理的改进[J].空军雷达学院学报,2003(4):46-47.
[3]冯滨鲁.Liapunov稳定性定理的推广[J].系统科学与数学,1998(2):211-214.
[4]徐道义,颜祥伟.关于部分变元渐近稳定性的几个基本定理[J].四川师范大学学报(自然科学版),1996(2):6-11.
[5]冯滨鲁.稳定性定理的推广[J].山东师范大学学报(自然科学版),1992(2):16-19.
[6]周康.关于部分变元的强稳定性的基本定理[J].华中师范大学学报(自然科学版),1995(1):24-26.
[7]孟新柱.部分变元的强稳定性研究[J].山东科技大学学报(自然科学版),2002(3):18-20.
[8]张维.微分系统关于部分变元的强稳定性[J].华中师范大学学报(自然科学版),1992(4):17-21.
[9]刘丹.关于部分变元的强稳定性[J].潍坊学院学报,2015(2):14-16.
Several Theorems of Strong Stability on Partial Variables
LIU Dan
(School of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao,266590,China)
The several theorems are given with respect to partial uniformly asymptotic stability and partial asymptotic stability under continuous perturbation,which improves and generalizes the existing conclusions in relevant literatures.
partial variables;strong asymptotic stability;continuous perturbation;strong uniformly stability
O175.21
A
1672-2590(2015)06-0030-04
2015-09-17
刘丹(1991-),女,黑龙江方正人,山东科技大学数学与系统科学学院硕士研究生.

