多偏差变元p-Laplacian方程周期解的存在性

陈仕洲

（韩山师范学院数学与统计学院，广东潮州 521041）

多偏差变元p-Laplacian方程周期解的存在性

陈仕洲

（韩山师范学院数学与统计学院，广东潮州 521041）

利用重合度理论研究了一类多偏差变元的p-Laplacian方程周期解存在性问题，获得了其周期解存在性的新结论，推广和改进了已有文献中的相关结论.

偏差变元；存在性；泛函微分方程；周期解；重合度理论

1 引言及引理

由于p-Laplacian方程具有较广泛的应用背景，因此一直受到人们极大的关注，也取得了许多很好的成果[1-10].但针对具有多偏差变元高阶p-Laplacian方程周期解存在性研究则不多，最近文[5]、[6]和文[7]分别研究了具有两个偏差变元方程

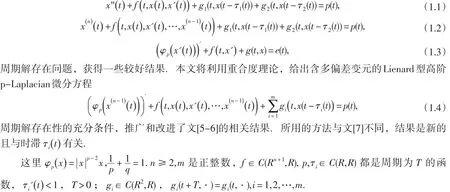
2 主要结论

[1]GAINES R E,MAWHIN J L.Coincidence degree and nonlinear differential equations[M].Berlin:Springer-Verlag,1977：95-169.

[2]黄先开，向子贵.具有时滞的Duffing型方程的2π周期解[J].科学通报，1994，39（3）：201-203.

[3]李永昆.具偏差变元的Lienard型方程的周期解[J].数学研究与评论，1998，18（4）：565-570.

[4]陈仕洲.具偏差变元高阶Lienard型方程周期解存在性[J].纯粹数学与应用数学，2006，22（1）：108-110.

[5]朱宏伟，王梅.具有两个偏差变元的广义Lienard型方程周期解存在性[J].青岛大学学报：自然科学版，2011，22（1）：5-9.

[6]陈世哲，陈仕洲.具有两个偏差变元高阶中立型微分方程的周期解存在唯一性[J].科学技术与工程，2012（11）：11-15.

[7]YANG Xiaojing，KIM Yong-In，LO Kueiming.Periodic solutions for a generalized p-Laplacian equation[J].Applied Mathematics Letters,2012,25：586-589.

[8]LI J W，WANG G Q.Sharp inequalities for periodic functions[J].Applied Mathematics E-Notes,2005（5）：75-83.

[9]PENG Lequn,LIU Bingwen,ZHOU Qiyuan.Periodic solutions for a kind of Rayleigh equation with two deviating arguments [J].Journal of the Franklin Institute,2006,343（7）：676-687.

[10]张志戎，鲁世平.一类具偏差变元高阶p-Laplace微分方程的周期解[J].吉林大学学报：理学版，2011，49（1）：71-75.

Existence of Periodic Solutions for a Kind of p-Laplacian Equation with Deviating Arguments

CHEN Shi-zhou
（School of Mathematics and Statistics,Hanshan Normal University,Chaozhou,Guangdong,521041）

By using the theorem of coincidence degree,existence of periodic solutions for a kind of p-Laplacian equation with deviating arguments is studied.Some new results for the existence of periodic solutions are obtained,which extend and improve the related reports in the literatures.

deviating argument；existence;functional differential equation;periodic solution;coincidence degree

O175.12

A

1007-6883（2015）06-0014-07

责任编辑 朱本华

2015-10-15

广东省高等教育教学改革项目（项目编号：GDJG20142396），韩山师范学院理科团队项目（项目编号：LT201202）.

陈仕洲（1959-），男，广东汕头人，韩山师范学院数学与统计学院副教授.