Nonsmooth Canards in Planar Fast-Slow Systems with Self-intersecting Critical Manifolds

XIE Feng(谢峰)，LUO Lingyao(罗玲瑶)

(Department of Mathematics，Donghua University，Shanghai 201620，China)

Abstract:In this paper，a class of piecewise-smooth planar fast-slow systems is considered.When the critical manifold has a self-intersection point，sufficient conditions for the existence of nonsmooth canards are obtained using asymptotic methods.Moreover，the asymptotic estimate of the control parameter for which a canard exists is obtained.

Key words:Piecewise-smooth fast-slow system;Canards;Slow manifold;Singular perturbation

1.Introduction

Canards in fast-slow dynamical systems are the trajectories which follows both an attracting slow manifold and a repelling slow manifold for a considerable amount of time.The classical canard phenomenon is first discovered by Benoˆıt et al.in a study of the van der Pol system using techniques from nonstandard analysis[1－2]，where canard cycles represent a special class of relaxation oscillators building a bridge between small amplitude limit cycles and large amplitude relaxation cycles.From then on，canards have gradually become an important topic in smooth fast-slow systems[3].Besides the van der Pol system，canards occurring in many chemical，biological and other models have been extensively investigated by using classical asymptotic methods and geometric methods;see for instance[4-10]and references therein.

Nonsmooth dynamical systems that contain nonsmooth functions of their arguments arise naturally in many fields，such as switching systems and impact oscillators.Research on canards in nonsmooth systems can be traced back to modelling electrical and electronic circuits by Japanese scholars in the early 1990[11－13].Recently，canards have also been found in piecewise-smooth van der Pol systems[14]modelling thermohaline circulation[15]and mixedmode oscillations in piecewise-linear fast-slow systems[16].Much attention has been paid to canards in piecewise-smooth systems，especially in piecewise linear systems[17－20].

Generally，there are two mechanisms behind appearance of canards in planar fast-slow systems with a perturbation parameter and a control parameter.One is that the critical manifold has a fold as in classical van der Pol system[1，21]and the other is that the critical manifold has a self-intersecting point as in[5].In smooth fast-slow system，canard phenomena，from the computaion of canard values to canard explosions，have been investigated thoroughly by various ways including nonstandard analysis，asymptotic analysis，and blow-up techniques.However，nonsmooth canards occurring in piecewise-smooth systems are not well understood yet，in particular，in the asymptotic estimate of control parameter for which a canard exists.As in[17]，the existence of nonsmooth canards are shown for suitable control parameterλdepending onε，but how to establish the asymptotic estimate ofλ(ε)，just as in the case of smooth systems，remains open.

As an important step towards this，in the present paper we are devoted to study the existence and asymptotics of nonsmooth canards which is due to the intersection of the critical manifold.The asymptotic estimate of the control parameter for which a canard exists will be obtained by classical asymptotic analysis method.These results can be viewed as a natural generalization of the corresponding smooth case[5].

The rest of the paper is organized as follows.In Section 2，the conditions and the main result are described.The proof of the main result and an example are given in Section 3.

2.Statements of the Conditions and the Main Result

We consider the planar fast-slow dynamical system

where for simplicity we assume thatfandgare independent ofε，and 0＜ε≪1 and|λ|≪1 are perturbation parameter and control parameter respectively.Assume thatf(x，y)∈C∞([x1，x2]×R)，g(x，y，λ)∈C∞([x1，x0)∪(x0，x2]×R×[-λ0，λ0])for certainx1＜x0＜x2andλ0＞0.By transforming from the slow time scaletto the fast time scaleτ=t/ε，one obtains the following equivalent fast system

Forλ=ε=0 the setΓ≡{(x，y)|g(x，y，0)=0}，which is called the critical manifold，corresponds to the equilibria of(2.2).Generally，the critical manifoldΓconsists of three nonintersecting parts:the attracting partΓ－at which all the eigenvalue ofhave negative real part，the breakoffpartΓ0at which the relation det=0 is satisfied，and the repelling partΓ+=Γ(Γ－∪Γ0).It follows from Fenichel’s invariant manifold theory[22－23]that a submanifoldpersists as a nearby locally invariant slow manifoldof(2.2)for sufficiently smallε.A canard corresponds to the intersection of an attracting and a repelling slow manifolds in the vicinity ofΓ0.In most common situations，Γ0is composed of folds or points of self-intersection of the critical manifoldΓ.In this paper，we focus our attention on the case that the critical manifold self-intersects at some point.

Let us describe the first assumption.

Assumption 1The critical manifoldΓof(2.1)consists of two piecewise-smooth curvesΓ1andΓ2intersecting at somex0∈(x1，x2)，whereandcan be expressed as

Moreover，Γ1is exactly composed of three nonintersecting parts:the attracting partthe repelling partand the breakoffpointx0.Fig.1 shows a general configuration of the critical manifold.

Fig.1 A general configuration of the critical manifold

Next，consider the reduced system of(2.1)

To describe canard trajectories of(2.3)，we denote byandthe projections on thex-axes ofandrespectively.The solution to the one dimensional equation

is denoted byx=x(t，x0)withx0=x(0，x0)，where

Assumption 2Each trajectory of(2.4)passesx0fromto.

Evidently，Assumption 2 implies that(2.4)has no equilibrium lying on[x1，x2].The trajectory of(2.3)

situates completely on the curveΓ1，which is a piecewise-smooth canard of the reduced system(2.3).An interesting problem is under what additional condition this canard can be perturbed to the corresponding canard of(2.1)forε＞0 by choosing suitableλ.To solve this problem，we present the following assumption.

Assumption 3The partial derivativesandexist，and

Remark 2.1The assumption(2.6)is usually non-degenerate condition，and(2.7)is a transversal condition as in the smooth case.For instance，it is easy to check thatg(x，y，λ)=y2-F(x)+λsatisfies Assumptions 1 and 3，where

Our main result is the following.

Theorem 2.1Let Assumptions 1-3 hold.Then，for small enoughε＞0 there exists aλ*(ε)withλ*(ε)=λ1ε+O(ε3/2)such that whenλ=λ*(ε)the system(2.1)has a canardy=(x)satisfying

whereφis defined in(2.5)andλ1will be defined in Section 3，and.

3.Proof of Theorem 2.1

To prove Theorem 2.1 we need the following lemma whose proof can be found in[24].

Lemma 3.1[24]Suppose that the functionsφ(x)，h(x)∈C∞[a，b]and satisfy the following conditions:

1)φ(x)enh(x)is integrable on[a，b]for anyn≥0;

2)h(x)has a unique maximal pointx=ξwithξ=a(b)and there exists an even numberm≥2 such that

Then，the following estimate holds asn→+∞:

whereφ(0)(ξ)=φ(ξ)andis theΓ-function.

Proof of Theorem 2.1Fenichel’s Slow Manifolds Theorem[22－23]implies that outside of any small neighborhood of the point(x0，φ1(x0))，the system(2.1)has invariant slow manifoldsandlying inO(ε)-neighborhood ofand，respectively.These slow manifolds are generally not uniquely defined.Thus，our problem can be reduced to local one of determining(in some small neighborhood ofx0)the trajectory of(2.1)whose endpoints lie onand.

With Assumptions 1 and 3 we can rewrite

where the factorωi(x，y)∈C∞(i=1，2)is nonzero at all points of the curveΓ1.Therefore，without loss of generality，we can assumeωi(x，y)＞0(i=1，2)，which corresponds to the disposition of the curvesΓ1andΓ2shown in Fig.1.(The caseωi(x，y)＜0(i=1，2)can be reduced to the case discussed above by substituting-yfory).After making the changez=y-φ(x)，the system(2.1)take the form

where=(φi(x)-ψi(x))(ωi(x，z+φi(x))-ωi(x，φi(x)))/zfori=1，2.

Fixing an arbitrary pointx∈[x1，x2]，denote byu(t，x)a solution of(2.4)with initial conditionu(0，x)=x.From Assumption 2，there is a unique timet=t(x).By the following transformations

the system(3.1)is transformed into the form

where the functionsγ1(s，z)andγ2(s，z)is sufficiently smooth，while for eachi=1，2，vi(s)，λΔi(s，z，λ)，Θi(s，z)andΛi(s，z)are obtained，respectively，from

under the change of coordinates mentioned above.Note that the system(3.3)is considered in a sufficiently small neighborhood of the origin.Therefore，in view of the first equation in(3.3)，we can eliminate the time variablet.As a result，we obtain

whereqis a small positive number.

From the above transformation，Assumption 3 andωi(x，φi(x))＞0，we know that

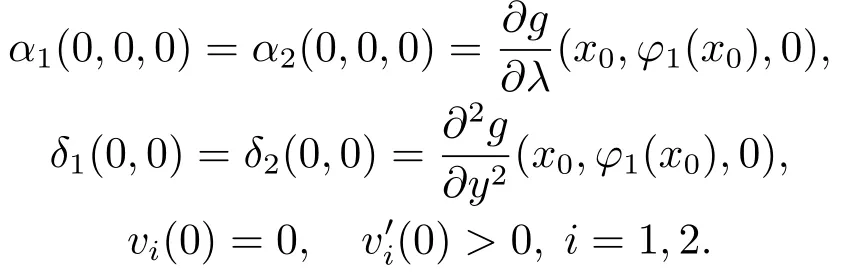
We define the Banach spaces as follows

with the sup-norm.

LetT1andT2be the operators onand，respectively:

Using the technique in[9]and the following inequalities

it is not difficult to verify that forλ=O(ε)，T1(T2，resp.)is a contracting map fromresp.)to itself.Hence，for eachλ=O(ε)there exists a unique solutionz－(x，ε)(z+(x，ε)，resp.)on[-q，0]([0，q]，resp.).In order that the solution to(3.4)is continuous atx=0，namely，z－(0，ε)=z+(0，ε)，we need to choose a suitable parameterλfor which there is a continuous solutionz=z(x，ε)defined on[-q，q].

Letz(x，ε)，x∈[-q，q]be a solution to(3.4)for suitable parameterλ.From(3.5)and(3.6)we have

Setting

in(3.7)and(3.8)，and using Lemma 3.1 we have

From the system of algebraic equations(3.9)-(3.10)，we get the unique root

Thus，we have proved that for sufficiently smallε＞0 there exists aλ*(ε)=λ1ε+O(ε3/2)such that(2.1)has a canardy=φ(x)+in some small neighborhood ofx0.To complete the proof of Theorem 2.1 we only need to extend the canard over the slow manifoldsandThis finishes the proof of Theorem 2.1.

Remark 3.1From(3.11)and(3.12)，we see that ifg(x，y，λ)are a smooth function，thenβ1(0，0)=β2(0，0).Consequently，λ1=-β1(0，0)/α1(0，0，0)and(x)=φ(x)+O(ε)，which is the same with the results in[5].

Remark 3.2The same method can be used to study the more general case when(2.6)is replaced with the following condition

Finally，as an illustration of Theorem 2.1 we give the following example.

ExampleConsider the following system

whereF(x)is given in(2.8).The critical manifold consists of four half-lines emanating from the origin(see Figure 2).

By the transformationsz=y-2xforx≥0 andz=y-xforx＜0，ands=arctanx，the system can be transformed into the form(3.4)for some positive numberq.In this example，

Obviously，the system(3.13)satisfies Assumptions 1-3.Therefore，it follows from Theorem 2.1 that for sufficiently smallε＞0 there exists aλ*(ε)withλ*(ε)=λ1ε+O(ε3/2)such that whenλ=λ*(ε)the system(3.13)has a canard.

Fig.2 shows the comparison between the canard and the critical manifold by numerical simulation whenε=0.05，λ=0.06931(λ1ε≈0.06397).The canard first follows the attracting part of the critical manifold，next the repelling part for a short while，and then jump off，to the other stable manifold.

Fig.2 When ε=0.05 and λ=0.06931，the comparison between the canard(red curve)and the critical manifold by numerical simulation