两阶段休假M/M/c排队驱动的流体模型性能分析

李子坤，徐秀丽

(燕山大学理学院，河北秦皇岛066004)

1.引言

流体模型是一个输入输出系统，其中流体受外部驱动系统控制连续地流入和流出一个缓冲器.如今的信息时代，传统的离散排队模型有很大的局限性，流体模型已经广泛应用于各个领域中，尤其在通信网络和计算机技术中起到颇为重要的作用.

Virtamo和Norro[1]研究了由M/M/1排队驱动的流体模型，并把驱动系统推广到了有限状态环境的排队系统.Sericola和Tuffin[2]考虑了一个具有有限或无限等待空间的马尔可夫队列驱动的流体模型，导出了一种计算稳态缓冲器容量的一种新方法.Kulkarni[3]提出了使用谱方法分析有限状态马尔可夫过程驱动的流体模型的理论框架.Nabli[4]研究了一般马尔可夫流体模型的瞬态解，并分析了其渐进行为.Malhotr等[5]对具有两个拥塞阈值控制的反馈流体队列进行了分析，得到了稳态下缓冲器占用率的表达式，缓冲区延迟分布和吞吐量.

近些年来，有学者将休假策略加入到流体模型的驱动系统中，MAO等[6]分析了多重休假M/PH/1排队驱动的流体模型，得到了稳态库存量的LST及空库概率.XU等[7]把文[6]中驱动系统的休假策略拓宽到工作休假策略，并给出平均吞吐量，服务器利用率及稳态库存量的均值表达式.考虑到更加复杂的实际情况，有学者将休假策略发展到两阶段休假的情况，YE等[8]研究了两阶段休假M/M/1排队驱动的流体模型，得到流体模型稳态库存量的LST，导出稳态缓冲器库存量的表达式.另一方面，把外部环境进一步推广到多服务台排队系统，XU等[9]分析了多重工作休假M/M/c排队驱动的流体模型，得到流体模型的性能指标.

太阳能LED路灯照明控制系统设计是当今城市亮化和市政优化的重要项目.在路灯太阳能充电过程中，天气变化会影响到太阳能的传送效率，从而导致太阳能转化率变慢或者没有太阳能进行转化，相当于传输系统处于工作休假或经典休假.在此基础上，本文构建了两阶段休假策略的M/M/c排队驱动的流体模型，该策略包括休假和工作休假两个阶段，导出流体模型的各项性能指标，分析参数变化对模型性能指标的影响，进一步将结果应用到路灯太阳能充电过程中，以提高充电效率，提高太阳能的有效利用.

2.驱动系统的基本描述

在驱动系统中，假设顾客到达时间间隔和正规忙期的服务时间分别服从参数为λ和μb的指数分布，当系统中的所有顾客都完成服务后，服务员进入一次随机长度的工作休假，工作休假时间服从参数θw的指数分布.在工作休假期间，服务员进入一种低速率服务的状态，此时的服务时间服从参数μv(μv＜μb)的指数分布．一次工作休假完成时，若系统中有顾客正在接受服务，则从低速率μv服务状态切换到正规忙期的服务率μb，重新开始服务被中断的顾客，系统进入一个正规忙期;否则，服务员进入正常休假期，正常休假时间服从参数θv的指数分布.一次正常休假完成时，若系统中无顾客，则继续进入下一次正常休假;否则，系统进入正规忙期.

假设到达时间间隔、服务时间、休假时间和工作休假时间两两相互独立.另外，采用先到先服务(FIFO)的排队规则.

设L(t)表示时刻t系统中的顾客数，J(t)=0，1，2分别表示时刻t系统处于休假期、工作休假期和忙期，则{L(t)，J(t)，t≥0}形成一个拟生灭过程，状态空间为Ω={(0，0)∪(0，1)∪(k，j)，k≥1，j=0，1，2}.将状态空间按照字典顺序排序，得到二维随机过程的无穷小生成元矩阵Q，即

其中

引理2.1[8]若系统负载ρ=λ/cμb＜1，则二次方程R2B+RA+C=0存在最小非负解

记二维随机过程{L(t)，J(t)，t≥0}的稳态分布为Ω，引入稳态分布向量π0=(π00，π01)，πk=(πk0，πk1，πk2)，k≥1，记x=(π0，π1，···，πc).众所周知，随机过程{L(t)，J(t)，t≥0}的稳态分布存在当且仅当二次方程R2B+RA+C=0最小非负解的谱半径SP[R]＜1，且xB[R]=0有正解，其中

由xB[R]=0可得方程组

为获得其稳态分布，引入函数分布

利用矩阵几何解方法，根据式(2.2)计算可得

定理2.1如果系统负载ρ＜1时，随机过程{L(t)，J(t)，t≥0}的稳态分布为

其中K=πc－1，0由归一化条件=1确定.

3.流体模型的构建与描述

设X(t)为缓冲器在t时刻的容量，则X(t)就是一个非负的随机变量.设缓冲器的净输入率(流入率-流出率)为三维随机过程{X(t)，L(t)，J(t)，t≥0}的函数

其中σ＜0，σ2＞σ1＞σ0＞0.驱动系统处于忙期时，缓冲器库存量以速率σ2增加;驱动系统处于工作休假期间，且驱动系统中有顾客存在时，缓冲器库存量以速率σ1增加;驱动系统处于休假期间，且驱动系统中有顾客存在时，缓冲器库存量以速率σ0增加;驱动系统处于工作休假或休假期间，且驱动系统中没有顾客存在时，缓冲器库存量以速率-σ减少，直至缓冲器库存量为空.保持这种状态直到系统中再次有顾客进入，一直按照这种规律循环下去.

流体模型的平均漂移为

其中πkj，(k，j)∈Ω，见定理2.1.由文[3]可知，当d＜0，ρ＜1，流模型是稳定的.记流体模型的稳态随机向量为(X，L，J)，这里的随机变量X为稳态下缓冲器的库存量.

设流体模型的稳态联合分布为

由全概率公式知，流体模型库存量的稳态概率分布为

运用标准化方法得到以下稳态联合分布Fkj(x)满足的矩阵微分方程组

满足边界条件

其中a=P{X=0，L=0，J=0}为稳态下缓冲器的空库概率.为了计算简便，记向量

则微分方程组(3.1)可写成以下形式

其中Λ=diag((σ，σ)，(σ0，σ1，σ2)，(σ0，σ1，σ2)，···).

如果直接用边界条件来解矩阵方程(3.2)是有些困难的，下面引入稳态联合分布和库存量稳态概率分布F(x)的LT变换如下

对方程(3.2)两边进行Laplace变换，利用边界条件整理得

4.流体模型的稳态分析

为了得到流体模型的稳态分布和性能指标，引入下面两个二次方程.

引理4.1[9]若驱动系统负载ρ＜1，对任意s≥0，二次方程cμvz2-(λ+θw+cμv+sσ1)z+λ=0存在两个实根β0(s)和β1(s)，且

易知0＜β0(s)＜1，β1(s)≥1，β0(0)=r，这里的r如(2.1)所示.

引理4.2[9]若驱动系统负载ρ＜1，对任意s≥0，二次方程cμbz2-(λ+cμb+sσ2)z+λ=0存在两个实根γ0(s)和γ1(s)，且

易知0＜γ0(s)＜1，γ1(s)≥1，γ0(0)=ρ，γ1(0)=1.

对任意s≥0，引入

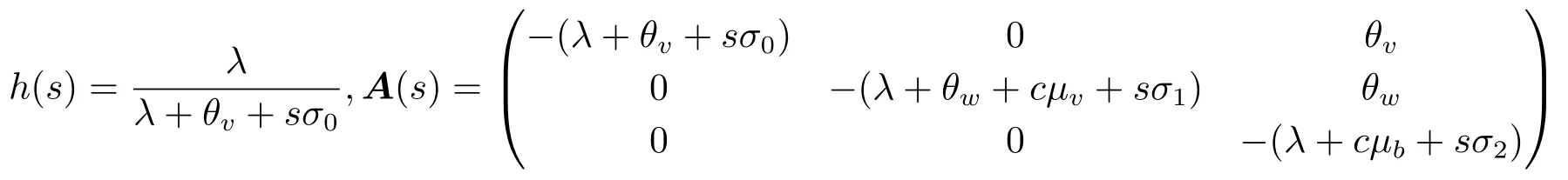
可得

定理4.1对任意s＞0，二次矩阵方程R2(s)B+R(s)A(s)+C=0存在最小非负解

其中

这里的β0(s)和γ0(s)见(4.1)和(4.2)，从(2.1)可知R(0)=R.

证由于B，A(s)和C都是上三角结构矩阵，设方程R2(s)B+R(s)A(s)+C=0中的R(s)有同样的上三角结构

将R(s)代入上面的二次方程中得到

上述各式依次记为(4.3.1)～(4.3.6).

从式(4.3.1)和式(4.3.2)可以得到

由式(4.3.4)和式(4.3.6)可以得到R22(s)=β0(s)和R33(s)=γ0(s)，这里的β0(s)和γ0(s)见(4.1)和(4.2).

把R11(s)=h(s)，R22(s)=β0(s)和R33(s)=γ0(s)代入到(4.3.3)和(4.3.5)中，给出

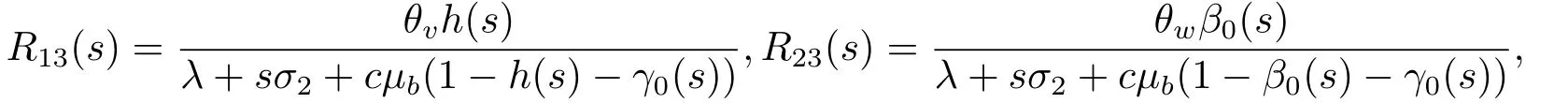
这里的R13(s)和R23(s)分别记作m(s)和g(s).因此，定理4.1推导完毕.

为了方便求解库存量及状态的稳态联合分布函数的LT，注意到矩阵方程(3.3)的结构，构造以下四个函数列

计算整理可得

定理4.2若ρ＜1和d＜0，库存量及状态的稳态联合分布函数的LT为

其中

证矩阵方程(3.3)可以写成下面的形式

“中国寻根之旅”活动对于培养华裔青少年的族群意识、促进华族文化认同、加强华族文化传承等方面都具有重要意义。而文化认同又是族群意识培养、文化传承的中心环节，华文教育的推动和发展又是实现文化认同的前提条件。

上述方程组依次记为(4.9.1)～(4.9.7).

若ρ＜1和d＜0成立，三维马尔可夫过程{X(t)，L(t)，J(t)，t≥0}存在唯一平稳分布{Fkj(x)，k，j∈Ω}[6].因此，方程组(4.9)存在唯一解.下面只需验证(4.8)满足(4.9).

首先对于k≥c，把代入式(4.9.7)中，得

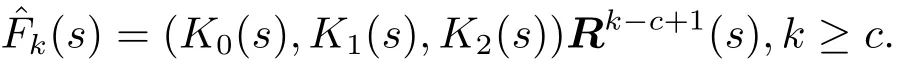
特殊地，当k=c时，有

其次由式(4.9.4)可知

定理4.3当ρ＜1和d＜0时，稳态下缓冲器库存量的空库概率及均值的表达式为

证将式(4.9.6)从k=2到k=c-1相加，得

移项合并得到

把(4.9.3)代入(4.10)，有

把式(4.9.1)，(4.9.2)和定理4.2中的表达式代入(4.11)，整理可得

由式(4.9.4)可知

进而流体模型库存量平稳分布F(x)的LT为

其中e为三维全1列向量.

由(4.1)和(4.2)可知，R(s)的特征值β(s)，γ0(s)和h(s)都小于1，所以其谱半径SP[R(s)]＜1，(I-R(s))是可逆的，且

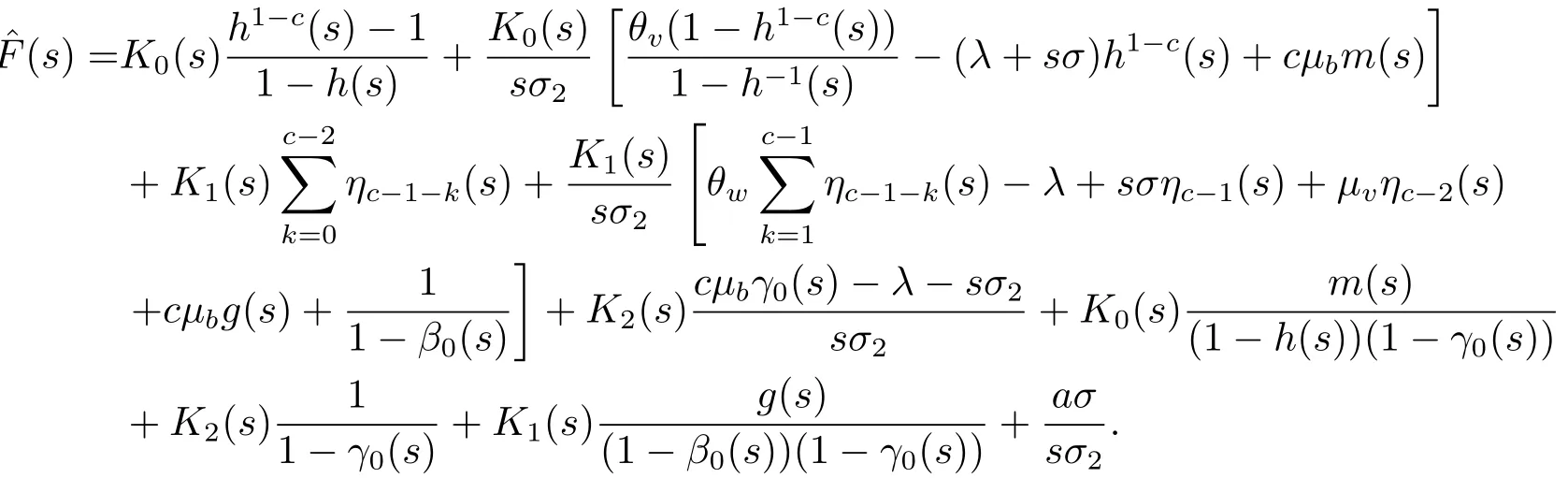
为了得到稳态下缓冲器库存量的均值，引入Fkj(s)，(k，j)∈Ω和F(x)的LST，记

进一步得到缓冲器库存量稳态分布的LST

对方程(4.12)两边同时求导，让s→0，求极限得到

整理可得

5.数值分析

考虑到路灯太阳能充电过程，把光照射到太阳能光伏板上多个点的过程看作一个多服务台的排队系统，转化成的电流相当于流体，太阳能光伏板就相当于流体缓冲器，稳定输送电流到蓄电池中.设太阳光到达光伏板上每个点的时间间隔服从参数为λ的指数分布.太阳光正常照射时，系统处于忙期，太阳能转化速率为μb;太阳光照较弱时，太阳能转化速率变为μv，相当于系统处于工作休假期间，工作休假时间参数为θw;阴天或者夜晚没有光照时，没有太阳能进行转化，系统处于经典休假期，休假时间参数为θv.在此实际应用中，由于不同季节的夜晚长短不同，休假时间参数θv会因季节的改变而改变.根据分析给出的流模型的空库概率和平稳库存量均值的表达式，通过调节参数变化控制系统性能指标的变化.

假设光伏板吸收太阳能的点数量为3.设λ=13，μv=0.5，θv=3，θw=2，σ0=1，σ1=2，σ2=3时，图1描述了光伏板中无电流的概率a随太阳能转化速率μb和净输入率σ的变化情况.观察图1可以得出，当μb一定时，光伏板中无电流的概率a随σ的增大而减小;当σ一定时，a随μb的增大而减小.

图1 a随μb和σ的变化

设λ=15，μb=3，μv=1，θw=0.5，σ0=1，σ1=2，σ2=3时，图2描述了光伏板中无电流的概率a随休假时间参数θv和净输入率σ的变化情况.观察图2可以得出，当θv一定时，光伏板中无电流的概率a随σ的增大而减小;当σ一定时，a随θv的增大而增大.

图2 a随θv和σ的变化

设λ=5，μv=1，θv=0.2，θw=0.1，σ0=1，σ1=2，σ2=3时，图3描述了系统的平均电流E(X)随太阳能转化速率μb和净输入率σ的变化情况.观察图3可以看出，当μb一定时，平均电流E(X)随着流入率σ的增大而增大;当σ一定时，平均电流E(X)随着μb的增大而增大.

图3 E(X)随μb和σ的变化

设λ=5，μb=4，μv=1，θw=0.2，σ0=1，σ1=2，σ2=3时，图4所示刻画了系统的平均电流E(X)随休假时间参数θv和净输入率σ的变化情况.观察图4可以得到，当θv一定时，平均电流E(X)随着流入率σ的增大而增大;当σ一定时，平均电流E(X)随着θv的增大而减小.

图4 E(X)随θv和σ的变化

由图1-4可知，在路灯太阳能中，若想提高太阳能的有效利用，降低能量损耗，必须要选择合适的太阳能装置以提高转化速率及不同季节时期的光伏板的电流传输率.

6.结论

本文研究了有两种休假状态的M/M/c排队驱动的流体模型，两种休假状态在一定条件下可以切换，运用拉氏变换的方法得到其稳态库存量的空库概率及均值表达式，并结合路灯太阳能充电过程，分析系统中的参数变化对模型各项性能指标的影响，以便提高太阳能的有效利用.