一类具记忆项和非线性阻尼项的双曲型方程的整体吸引子
张素丽,张建文,王海燕
(1.太原理工大学机械与运载学院,山西太原030024;2.太原理工大学数学学院,山西太原030024;3.太原科技大学应用科学学院,山西太原030024)
1.引言
波动方程是偏微分方程中重要的一类方程,对波动方程的数学研究能帮助我们更加准确深刻地描述和理解物体的运动情况和物理规律.关于波动方程的研究已有很多著作.[1-3]Giorgi等[4]研究了只有记忆项的波动方程

的整体吸引子的存在性.记忆项是反应系统的过去状态对系统的未来行为的影响,是材料的某种“记忆”性能,很多粘弹性材料都有这种“记忆”性能.
MA和ZHONG[5]研究了具有记忆项和弱阻尼项的波动方程

的整体吸引子的存在性.由于在物体的运动过程中,阻尼是不可避免的,并且阻尼对物体的运动有着巨大的影响,所以研究具有阻尼项和记忆项的波动方程有很重要的物理意义.
Park等[6]研究了具有记忆项和非线性阻尼项,即阻尼项以非线性次数增长情形下的波动方程

的整体吸引子的存在性.
Kirchhoff[7]于1883年研究可拉伸弦的振动问题时,建立了下列模型

与经典波动方程相比,这类方程能更准确地描述弦自由振动问题.因此,后人将这类方程命名为Kirchhoff方程.关于此类问题解的存在性证明可参考文[8-10].2011年Lazo[11]运用经典的Galerkin方法证明了具有记忆项的Kirchhoff方程

的整体弱解的存在性.
受以上文章的启发,我们研究如下一类具有记忆项和非线性阻尼项的Kirchhoff波动方程的整体吸引子的存在性.

Ω是RN中具有光滑边界∂Ω的有界区域,其中M(s)=a+bs,a,b>0,g(ut)是阻尼项,f(u)是源项.关于a(x),g(ut),f(u)的假设我们将在后面给出,h是L2中的函数.
我们采用文[4-6]中的定义:

对上式求导,我们可得

所以

令μ(s)=-K′(s),K(∞)=1,方程(1.1)变为

初边值为
2.预备知识
我们首先给出证明过程中用到的一些假设:
1)关于记忆项μ的假设:
(h1)μ(s)∈C1(R)∩L1(R),∀s∈R+;
(h3)μ(s)≥0,μ′(s)≤0;
(h4)μ′(s)+k1μ(s)≤0,∀s∈R+,其中k1>0.
2)函数a(x)满足

其中α0是常数.
3)函数f∈C1(R),满足


当n≤2时,0<p<∞;当n>2时,λ1是中的第一特征值.
4)函数g满足

当n≤2时,1≤q<∞;当n>2时,1≤q≤.
接下来,我们给出本文用到的空间

其内积和范数为

我们的分析是基于如下空间

并对其赋予以下的范数

利用经典的Galerkin方法,我们可得到如下关于系统(1.7)-(1.10)解的存在唯一性,具体可参考文[6,14].
引理2.1[6,14]假设1)-4)都成立,若z0=(u0,v0,η0)∈H,则系统(1.7)-(1.10)存在唯一弱解z=(u,ut,η),对所有的T>0都满足z∈C([0,T],H).
引理2.2[13]设g(.)满足(2.4).则对任意δ>0,存在C(δ)>0,满足

3.吸收集
本节中,我们将证明系统(1.7)-(1.10)在H中存在有界吸收集.本文中(·,·),||·||分别代表L2中的内积和范数,Ci表示不同的正常数.
引理3.1在引理2.1的假设下,系统(1.7)-(1.10)在空间H中存在有界吸收集.
证方程(1.7)与ut作L2中内积,得

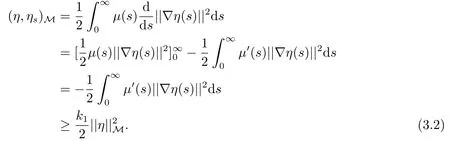
我们令

由(3.1),(3.2)我们可知

对上式,我们在[0,T]上积分,由假设2),4),我们有

由假设2),我们可知存在λ>λ′>0,以及C0满足下式


选择足够小的ε>0,则

由(3.3),(3.6),可得

接下来,方程(1.7)与v=ut+δu作L2中内积,我们可得
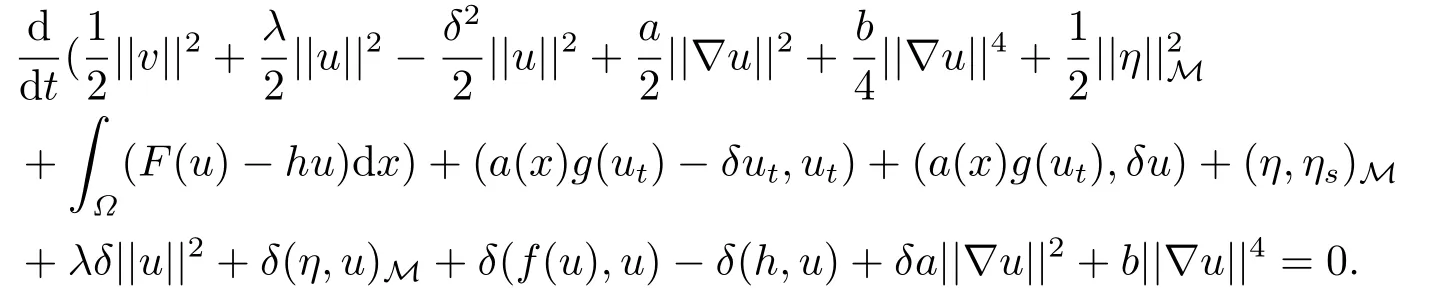
设

所以

利用(3.5)和Young不等式,
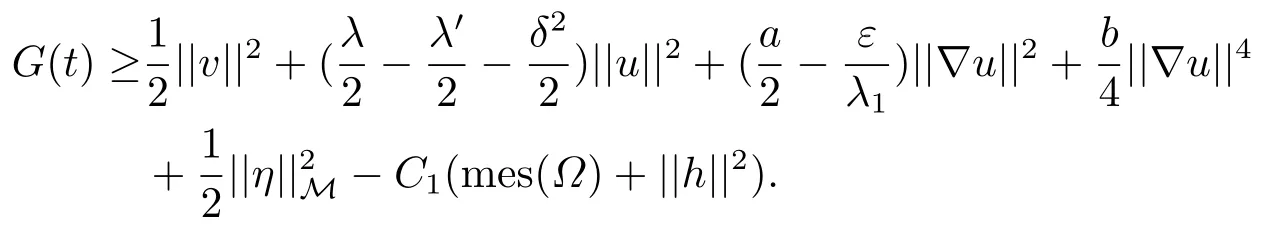
选择足够小的δ,ε,使得,则有

由假设2),4),我们可知存在δ>0和C(δ)>0,使得下式成立


由Young不等式,可得

由假设4),我们有

所以

其中C是与s无关的常数.

其中a0=supx∈Ω a(x),γ是常数.由(3.5)(3.10)(3.11)(3.13),我们有
选择足够小的γ,使得可知

其中CE(0)由δ,Cγ,Cs,E(0)共同决定,是依赖于δ,Cδ,C0,C的常数.


对(3.8)在(0,t)上积分,结合(3.7),(3.9),(3.14),我们可得

其中δ′=min{δ,k1}.

因此B0是一个有界吸收集,定义

B1就是所需的有界吸收集.证毕.
4.整体吸引子
本节我们将证明系统整体吸引子的存在性.我们定义
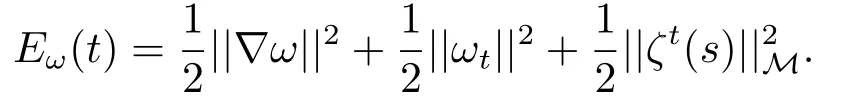
引理4.1[12]耗散动力系统(H,S(t))具有一个紧的整体吸引子当且仅当它是渐进光滑的.
引理4.2[12]假设对任意的有界正不变集B⊂H和任意的ε>0,存在T=T(ε,B),使得

这里ΦT:B×B→R,对任意{zn}n∈N⊂B,满足

那么半群S(t)是渐进光滑的.
接下来,我们利用先验估计来证明系统的渐进光滑性.

首先,方程(4.2)与ω作L2中内积,有

对上式在[0,T]上积分


由Young不等式,我们有

紧接着,方程(4.2)与ωt作L2中内积,得

令

由于

所以

(4.6)在[s,T]上积分,其中0≤s≤t,

(4.7)关于s在[0,T]上积分,得


将(4.6)在[0,T]上积分,得

由(4.4)(4.5)(4.9),我们有

由(3.7)及吸收集的存在性,我们有

其中Cρ由mes(Ω),||h||2及B0的半径共同决定.
类似于(3.13),我们有


结合(4.8)(4.10)(4.12),我们有
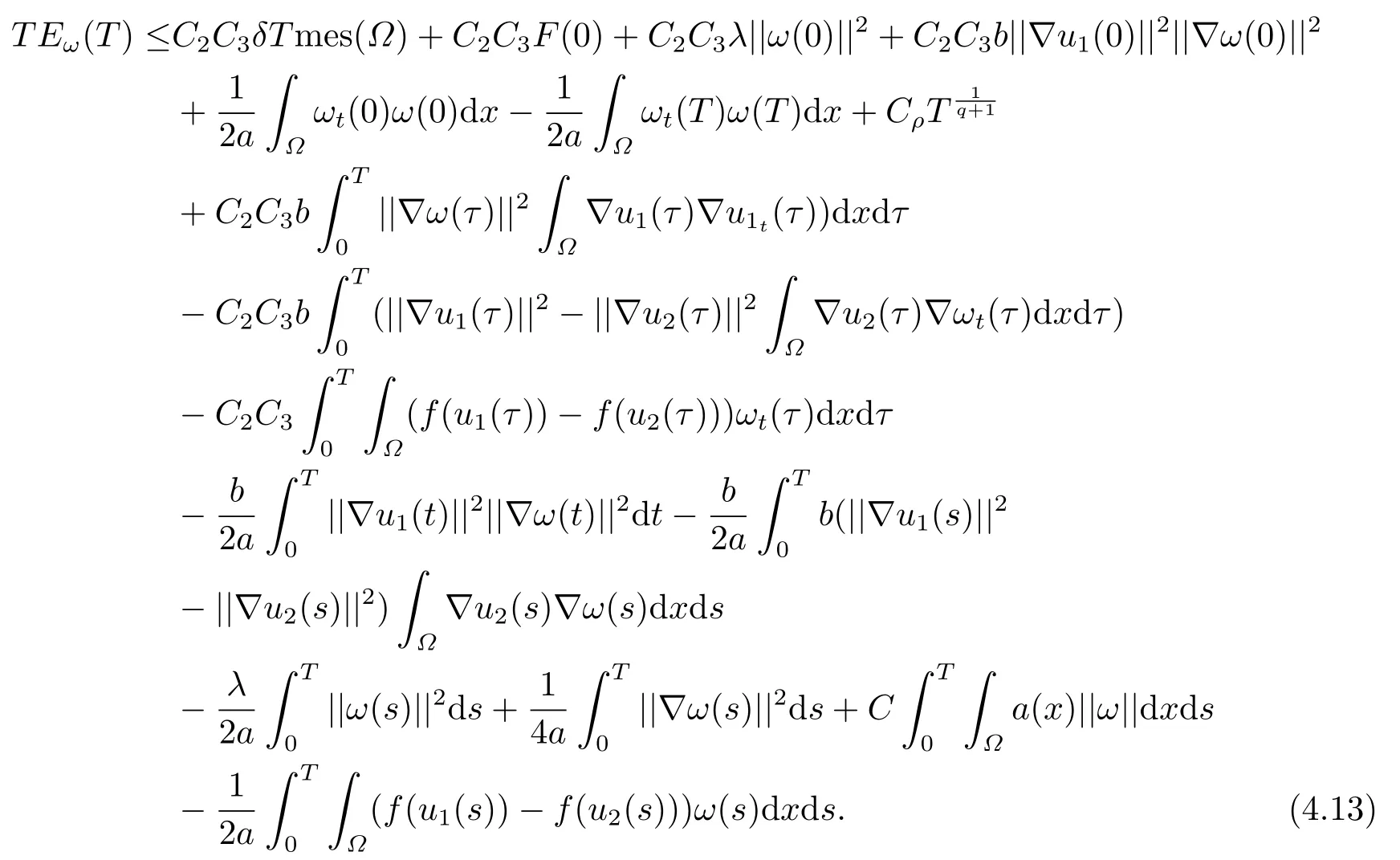
令

则我们有

接下来,我们利用引理4.2来证明半群{S(t)}t≥0在H中是渐近光滑的.
定理4.1在假设1)-4)下,系统(1.7)-(1.10)所对应的半群{S(t)}t≥0在H中是渐近光滑的.
证由于半群{S(t)}t≥0存在有界吸收集,我们选取并且选取足够大的T使得于是,由引理4.2,我们只需证明,(4.15)中定义的对每个固定的T,(4.1)式恒成立.这里(un,unt,ηn)是相应于初值=1,2的解,我们有和其中.
因为B1是H中的正不变集,不失一般性,我们有


紧接着,由(4.17),我们可得

最后,类似于文[6],我们有

结合(4.21)-(4.29)和引理4.2可知定理4.1成立.证毕.
定理4.2若假设1)-4)成立,系统(1.7)-(1.10)在H中存在整体吸引子.
证由引理3.1和引理4.1可知系统存在整体吸引子.证毕.

