fmKdV Equation for Solitary Rossby Waves and Its Analytical Solution

CHEN Liguo(陈利国)，GAO Feifei(高菲菲) LI Linlin(李琳琳)，YANG Liangui(杨联贵)

(1.School of Statistics and Mathematics，Inner Mongolia University of Finance and Economics，Hohhot 010070，China;2.School of Mathematical Sciences，Inner Mongolia University，Hohhot 010021，China)

Abstract:In this paper，based on the geostrophic potential vorticity equation of shallow water model describing the nonlinear Rossby wave，we derive a forced modified Korteweg-de Vries(fmKdV)equation by utilizing the reduced perturbation method.By analyzing the fmKdV equation，we can explicate the basic topography，which is an important factor for the formation of solitary Rossby waves，while slowly varying topography with time is an external forcing effect.Besides，the generalized bate and basic shear flow effect are also important factors in the generation of solitary waves.Finally，the analytical solution for the fmKdV equation are presented by the general mapping deformation method.The results show that slowly varying topography with time only affects the speed of Rossby waves，dissipation affects both the amplitude and speed of Rossby waves.

Key words:Rossby waves;fmKdV equation;Slowly varying topography;Dissipation;General mapping deformation method

1.Introduction

There are many nonlinear waves in the atmosphere，however，Rossby waves are important large-scale long waves，and they are a permanent fluctuation with a long life history and consistent structure，and they have the characteristics of stable and large amplitude solitary waves.Historically，many Nonlinear Partial Differential Equations(NPDEs)were used to characterize the generation and evolution of Rossby wave，and to reveal some physical mechanism of Rossby waves.The KdV equation is first derived to describe the generation of Rossby wave in barotropic fluids[1].Benney studied further Rossby solitary waves and generalized Long’s conclusions[2].Next，Redekopp and Weidman obtained the KdV equation and modified KdV(mKdV)equation with stronger nonlinearity，respectively，to describe the evolution of Rossby wave in stratified fluids[3－4].Ono[5]obtained Benjamin-Ono(BO)equation for algebraic Rossby wave.Many studies have shown that Rossby waves affect the planet’s weather and climate change，such as Gulf Stream vortices in the ocean，blocking patterns in the atmosphere，the red spot in the atmosphere of Jupiter，Southern Oscillation，etc.[6－9]Therefore，the theoretical study on Rossby waves can provide a theoretical basis for actual weather and ocean forecasting.

In complex atmospheric motions，the formation and decay of Rossby waves are influenced by many physical factors，such as beta plane approximation，dissipation，topography，external source，basic flow.Scholars use the mathematical model equations to explain these factors and reveal the nature of the wave phenomenon.YANG[10]concluded that the variation of beta，basic flow and topography could cause the changes of the Rossby wave packet.Vanneste[11]studied the change of Rossby wave frequency with a small-scale two-dimensional topography.CHEN[12]obtained a forced nonlinear Boussinesq equation under the combined action of the topography and dissipation.JIANG[13]discussed the influence of topography and dissipation on the Rossby waves.MENG[14－15]studied solitary Rossby waves induced by the dissipation，topography via Boussinesq equation and mKdV equation.Next，LIU[16]and SONG[17]presented the generalized beta plane approximation which can stimulate solitary waves without considering basic shear flow.

Numerous researchers have shown that topography has an extremely important influence on Rossby waves for the motion of the atmosphere at middle-high latitudes.Thus，for many years，there are many reports about the influence of topography on Rossby wave.the study of the effect of topography on Rossby solitary waves has been more active.Under the influence of global environmental change，such as global warming，topography will vary slowly with time，which affects the atmospheric movement and causes climate change.The physical mechanism of Rossby solitary wave can better describe some weather phenomena in the atmosphere.Therefore，the influence of varying topography on the solitary Rossby waves has attracted considerable research attention[18－21].However，forced mKdV equation with dissipation and slowly varying topography describe solitary Rossby waves has not been examined.

In the present study，we derive a equation to study the physical mechanism of Rossby waves in the barotropic atmosphere.The rest of the paper is organized as follows:In Section 2，we derive a fmKdV equation by employing the reduced perturbation method from a quasi-geostrophic barotropic potential vorticity equation under the generalized beta plane approximation.Also，we analyze the important physical factors that induce solitary Rossby waves.In Section 3，we mainly explore the analytical solution for the fmKdV equation.Then，based on the analytical solution obtained，we discuss the effects of dissipation and slowly varying topography on the speed and amplitude of solitary waves.Conclusions are presented in Section 4.

2.Derivation of the fmKdV Equation

From shallow water model，the dimensionless quasi-geostrophic barotropic potential vorticity equation under the generalized beta plane approximation，including topography，dissipation and external source is obtained as follows[15，22]:

whereψis the total stream function，β(y)yis the generalized beta approximation[17].h(y，t)=h0(y)+ϵh1(t)，h0(y)is the basic topography，h1(t)is slowly varying topography with time，ϵis a small parameter，which describes the slow degree of the topography over time.λis a dissipative coefficient.Qis the external source.∇2denotes the two dimensional Laplace operator.

The lateral boundary conditions are

Assume that the total stream function is

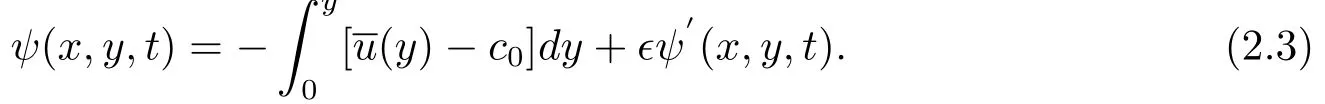
To balance between dissipation and nonlinearity，and eliminate dissipation caused by basic shear flow，we assume

We adopt the reduced perturbation method

Substituting Eqs.(2.3)-(2.5)into Eqs.(2.1)and(2.2)，we obtain

We adopt the weak nonlinear long wave approximation，and assume

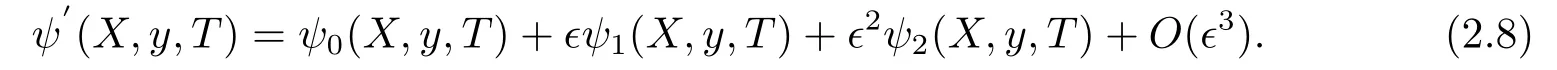
Substituting Eq.(2.8)into Eqs.(2.6)and(2.7)，we obtain the lowest-power and first order expansion ofϵas follows:

and

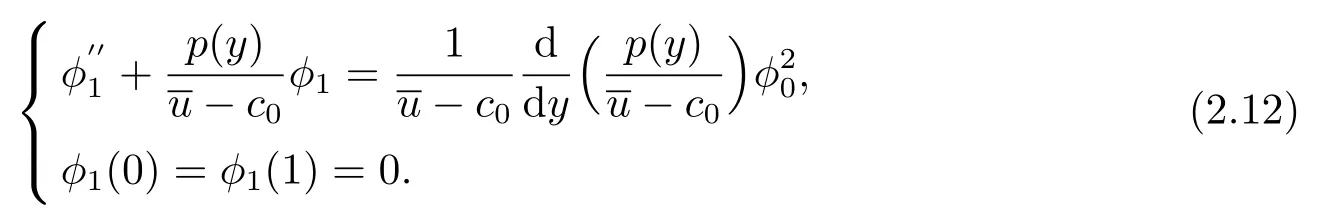
For the two-order expansion ofϵ，we obtain

where

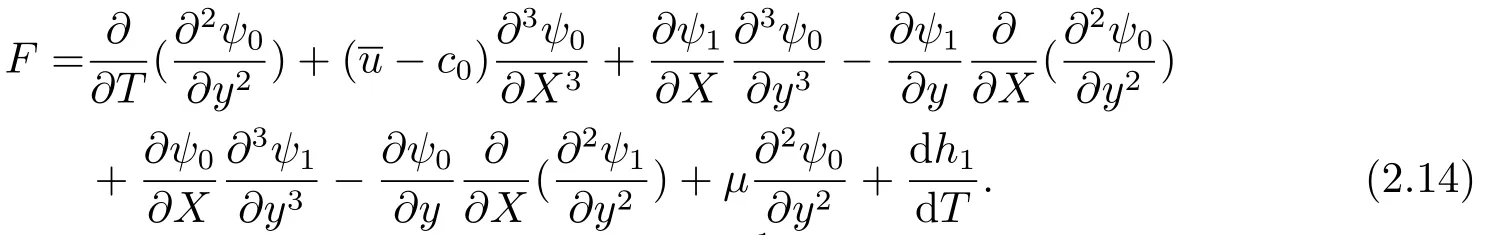
For Eq.(2.13)，using the solvability conditionFdy=0，we obtain fmKdV equation as follows:

where

Remark 2.1φ0andφ1are determined by Eigenvalue Eqs.(2.11)and(2.12).α1is the nonlinear coefficient，andα2is dispersion coefficient.The theoretical analysis of the Eqs.(2.11)and(2.12)，the effects of the generalized beta，basic topography，and basic shear flow，which are all essential factors to induce solitary Rossby waves.Note thatα10 whenthat is，basic topography can also induce the formation of solitary waves even without the generalized beta and shear basic flow.It also shows that solitary waves are closely related to topography.μArepresents dissipation term.H(T)represents the time forcing term，caused by slowly varying topography.In the following，we further explain the influence of slowly varying topography with time on Rossby wave.Whenμ=0 andH(T)=0，Eq.(16)is classical mKdV equation[3].Therefore，Eq.(2.15)is called fmKdV equation.

3.Analytical Solution

In recent years，researchers have obtained the analytical solutions of the NPDEs using different methods.[23－24]In order to reveal the feature and influence mechanism of solitary waves，we aim to obtain analytical solution of the fmKdV equation by employing the general mapping deformation method[25].

We perform the following transformation

whereK=K(T)andω=ω(T)are functions to be determined.Substituting Eq.(3.1)into Eq.(2.15)yields

Using the general mapping deformation method，we assume that the solutions of Eq.(3.2)as follows:

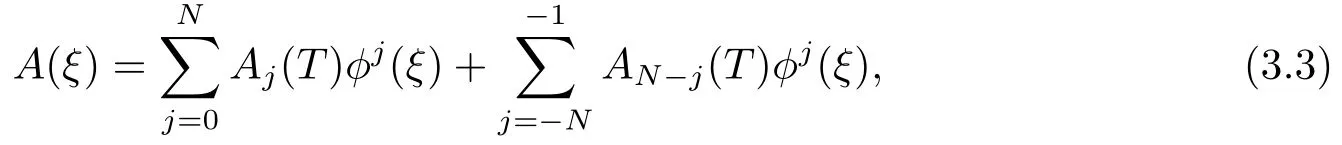
whereAi(T)，AN－j(T)(i=0，1，···，N;j=-N，···，-1)are functions to be determined.φ(ξ)is a solution to the following ordinary differential equation with variable coefficients:

whereaj=aj(T)(j=0，1，2，3，4)are arbitrary function ofT.By balancing between the nonlinear term and highest linear derivative，we obtainN=1.Eq.(3.3)is rewrited as follows

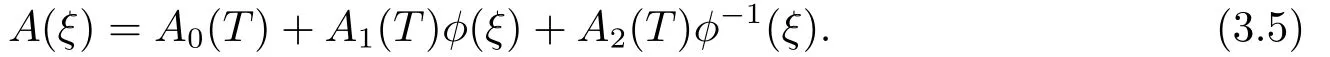
Substitute Eq.(3.5)into Eq.(3.2).Set the coefficients ofφj(ξ)andequal to zero.And the algebraic equations forA0(T)，A1(T)，A2(T)，K(T)，ω(T)are obtained.Then

Case 1

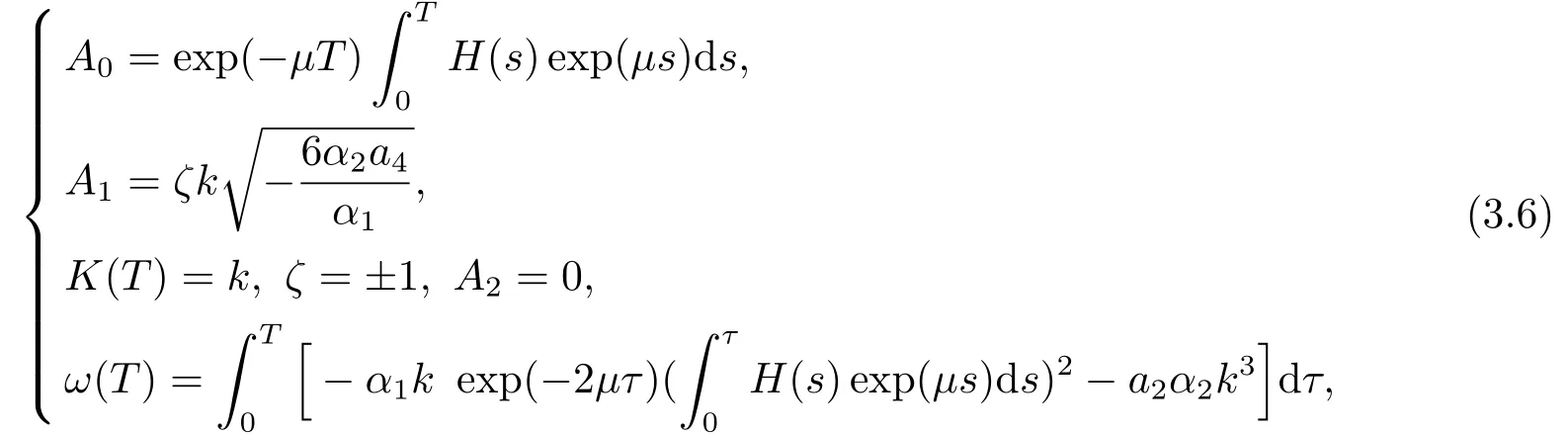
wherekis constant，a0=0，a1=0，a2is arbitrary constant，a3anda4satisfy the following conditions

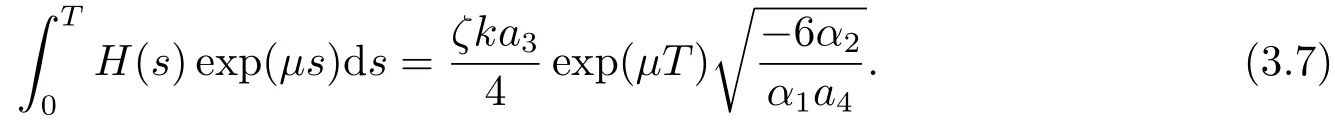
Case 2

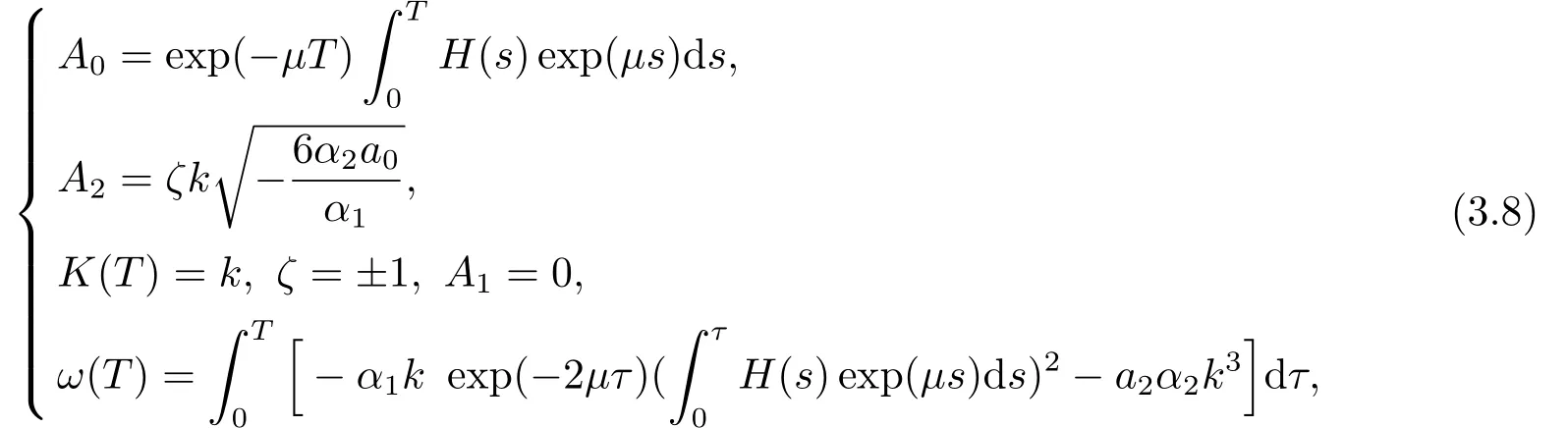
wherekis constant，a4=0，a3=0，a2is arbitrary constant，a1anda0satisfy the following conditions

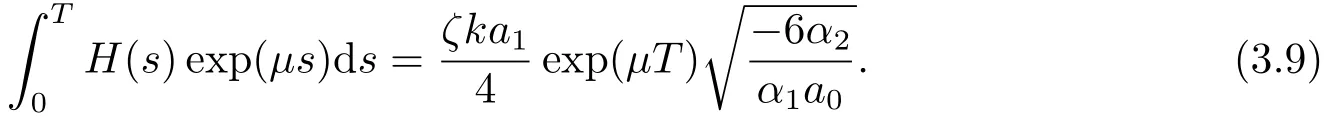
Corresponding to the solutionsφ(ξ)of Eq.(3.4)in[25]，the analytical solution of Eq.(2.15)is obtained.

and

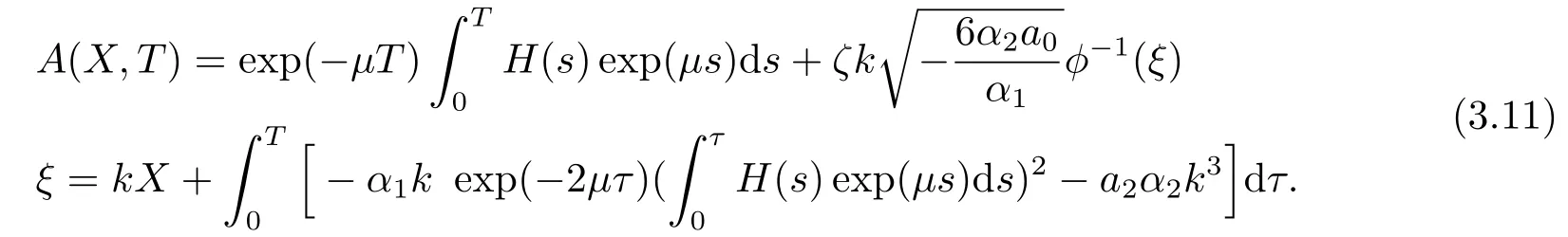
The velocity of solitary wave is

Remark 3.1The signs ofα1andα2are opposite.In the actual atmosphere motion，slowly varying topography with timeH(T)and dissipationμare very small，Therefore，Eq.(3.12)is significant.From the theoretical analysis of Eq.(3.10)-(3.12)，it can be seen that slowly varying topography with time only affects the velocity of Rossby solitary waves，but dissipation affects both the amplitude and velocity of Rossby solitary waves.

In the following，the influence of dissipation and topography on Rossby evolution is further explained through the evolution of Rossby amplitudeA(X，T)and velocityCs.According to[25]，takingh1=h10exp(MT)，and substituting them into Eq.(3.10).Taking the parameter ash10=0.2，M=-0.2，μ=0.01，k=ζ=1，a0=0，a1=0，a2=1，a3=-2，a4=1，α1=1，α2=.

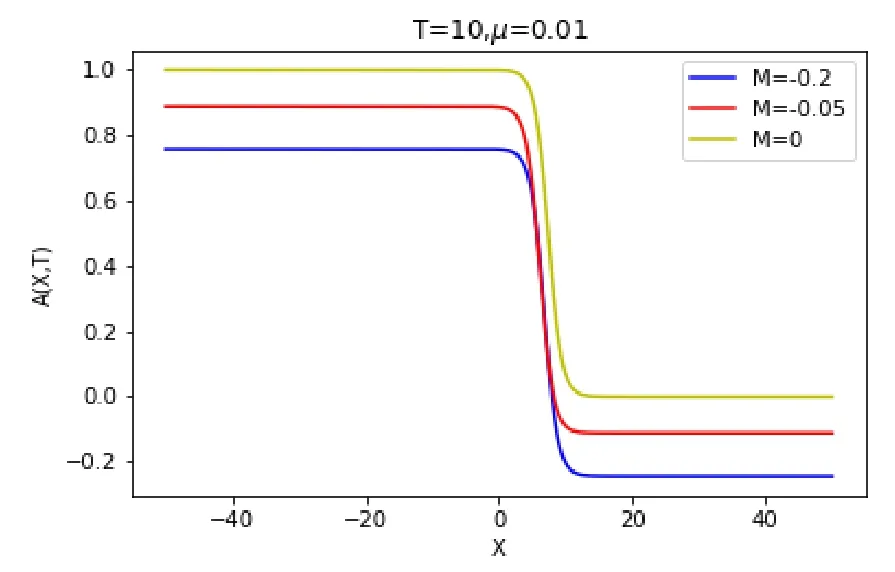
Fig.3.1 The evolution of A(X，T)under the influence of topography，where h10=0.2.

Fig.3.2 The evolution of A(X，T)under the influence of dissipation，where h10=0.2

From Figs.3.1-3.4，it can be seen that slowly varying topography and dissipation affect both the amplitude and velocity of Rossby solitary waves.

4.Conclusion

The fmKdV equation is fully displayed for describing the nonlinear solitary Rossby waves based on dimensionless geostrophic barotropic potential vorticity equation，using the reduced perturbation.We investigate physical mechanisms of Rossby waves by analyzing the effects of the generalized beta，dissipation，topography，and basic shear flow on the evolution of Rossby waves.In conclusion，the generalized beta，basic topography，and basic shear flow are essential factors to induce nonlinearity in Rossby waves.However，basic topography can induce solitary waves even without the generalized beta and shear basic flow.In addition，dissipation and slowly varying topography with time is forcing factor.Moreover，we obtain the analytical solution of the fmKdV equation by using the general mapping deformation method.Based on the solution and figures，we obtained the conclusion that slowly varying topography with time only affects the speed of Rossby solitary waves and dissipation affects both the amplitude and speed of Rossby solitary waves.

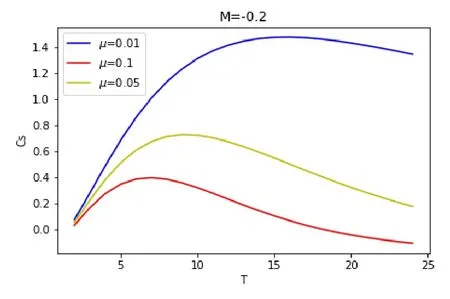
Fig.3.3 The velocity of solitary wave under the influence of dissipation，where h10=1

Fig.3.4 The velocity of solitary wave under the influence of topography，h10=1.