时间分数阶Fisher型非线性种群扩散模型的近似解
贾红刚,聂玉峰,赵艳敏
(1.许昌学院数理学院,河南许昌461000;2.西北工业大学数学与统计学院,陕西西安710072)
1.引言
分数阶微积分是一个古老而新鲜的概念.事实上,在整数阶微积分创立初期,就有一些数学家,如:Leibniz等开始考虑它的含义.在过去几十年里,随着科技发展,分数阶微积分开始应用到物理、种群扩散、控制、经济学、生物医学工程等领域。
种群扩散是生物的数量以及分布变化的反映.它主要研究种群密度或数量的动态改变.国内外已经有很多有关种群扩散模型的研究报道,但是这些研究往往采用整数阶微积分模型,近年来,鉴于分数阶微积分扩散模型所有的非局部性和时间遗传记忆性,使得它得到了普遍关注注,因为它更能全面客观地反应种群扩散演变规律.因此,分析时间分数阶种群扩散模型对于研究生物种群理论有着非常重要的价值.
1991年欧阳颀[1]提出了二维Turing斑图及分岔,从实验角度阐释了种群扩散现象.2004年,Wazwaz等[2]研究了一些Fisher方程的Adomian分解近似解,并分析了此近似解的变化对种群扩散的影响.2020年,Manimaran等[3]采用Faedo-Galerkin方法得到了一种时间分数阶种群相互作用模型的解.
同时,国内学者对于种群扩散分数阶模型问题也有报道,2003年,廖世俊[4]采用同伦分析法(homotopy analysis method),通过利用合适的映射,得到了模型问题的解.2004年,马知恩等[5]采用动力学模型局部地分析了病毒与免疫系统的演变趋势.2008年,刘发旺等[6-7]利用Adomian分解法研究了时空分数阶扩散模型方程.2009年,马军海、刘艳芹[8]利用分数阶理论、同伦扰动等方法法研究了一种非线性扩散方程径向对称方向的精确解.2011年,马军海、刘艳芹[8]利用分数阶微积分算子得到了分数阶非线性单种群和分数阶非线性两种群扩散模型,并运用此扩散模型结合同伦扰动法和变分迭代法得到了一类相应种群扩散问题的近似解.2019年,吴春等[9]采用分离变量法分析了非线性时间分数阶生物种群模型.
但是,国内外研究人员通过构造分数阶模型分析种群扩散问题的报道不多,比如,并且以上这些研究往往对应的分数阶种群扩散模型的为线性源函数,而对于分数阶种群扩散模型的源项为非线性的研究鲜有报道,所以,研究带非线性源项的时间分数阶种群扩散的研究很有意义.
2.分数阶非线性种群扩散模型相关理论简介
分数阶微积分已经得到了越来越多的关注和应用.如今,它已经被广泛地应用到粘弹性力学、热传导、电子信息、控制科学及生物种群扩散模型等学科中,分数阶微积分的定义很多,为方便研究,这里,我们仅仅阐释以下几种常见的分数阶微积分定义.
定义2.1[10]函数f(t)的α阶Riemann-Liouville分数阶积分定义:
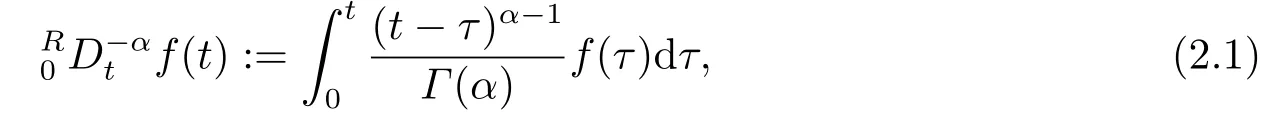
其中,α(Re(α)>0)是任意数,Γ(·)为Gamma函数.
定义2.2[10]可导函数f(t)的α阶Caputo阶分数阶导数定义:
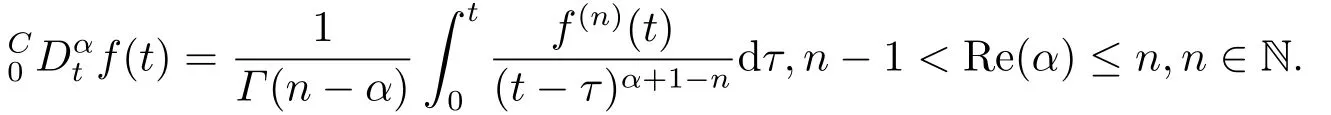
从Caputo分数阶导数定义可知,它能很方便地应用在初值问题中.
定义2.3[11]可导函数f(t)的α阶Abdeljawad分数阶导数定义:
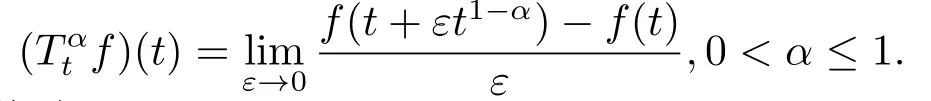
易知,当f(t)为可导函数时,

定义2.4[11]Abdeljawad分数阶积分定义:

并且有

这里,为方便研究,仅仅讨论单种群扩散模型的解法,扩散模型[12]是用来分析多种群相互作用关系、竞争关系以及种群与环境之间存在的相互关系的模型,种群扩散微积分模型有两种:线性和非线性模型,根据模型的分析方法,我们还可以分为两类:连续性和离散性扩散模型,应用广泛的连续性模型有:Logistic单种群模型、单种群反应扩散模型以及两种群间扩散模型[18],本文仅仅研究了单种群反应扩散模型.
3.种群扩散模型的求解
鉴于种群生态种群扩散的复杂性,并考虑到分数阶导数的优越性,这里,我们首先给出推广的时间分数阶Fick扩散定律[13]:

其中,J表示扩散通量.
引入质量守恒方程:

将方程(3.1)带入方程(3.2),可得含源项的推广的时间分数阶种群扩散非线性Fisher型模型方程:

其中,u=u(x,t)为种群密度函数,源项为种群增长项,且满足F(0)=F(0)=0,F′(0)>0>F′(1),方程(3.1)、(3.2)、(3.3)中所用的导数定义为Abdeljawad导数(带常数初值的变分迭代法求解u1时除外).
本文首先分别利用分数阶变分迭代法和同伦扰动法求解了一类时间分数阶Fisher型非线性扩散模型的近似精确解,并对近似解进行了讨论,进而得出:当分数阶导数阶数α→1时,本文方法求出的近似解与相应整数阶方程的结果是一致的,因此,可以验证本文所用方法的合理性和准确性.
我们分别利用分数阶变分迭代法[14]和同伦扰动法[15]来求解时间分数阶Fisher型非线性扩散模型方程.分数解变分迭代法求解过程如下:
首先,由方程(3.3),给出如下变分迭代关系[13]:

其中,λ(ξ)为拉格朗日乘子,这里取m=2,1<α≤2进而利用变分迭代法[16]可确定λ(ξ)=-1.因此得到方程(3.3)的变分迭代格式:

进而,我们从(3.5)的初始近似值起,开始迭代,并利用软件Mathematica计算,求出模型方程近似解.
问题1解下面的满足常初值条件的时间分数阶非线性Fisher型扩散方程:

然后,我们首先利用分数阶变分迭代法求解方程(3.6)-(3.7),变分迭代格式为:

根据上式,从u0开始迭代,u1的求解使用Caputo分数阶导数定义,u2,u3,···,un的求解使用Abdeljawad分数阶导数定义,可得如下一系列近似解:


接下来,我们用同伦扰动法求解此问题,求解过程如下:
建立下面的同伦格式[8]:

其中,u0为模型方程近似初始值,假设方程有级数解形式为;

将(3.14)带入(3.13),并比较等式两边p的同次幂得到:

用Abdeljawad分数阶积分定义分别对上述方程两边求积分,得

从而,根据同伦扰动法,可得方程(3.6)-(3.7)的近似解如下:

若对上述解取α→1时的极限,可得

上面的解与整数阶Fisher种群扩散模型的精确解[17]结果是一致的,这说明本文所用方法是合理准确的.
问题2求如下时间分数阶非线性Fisher型扩散方程

满足如下初值条件

由上面两式,得相应时间分数阶变分迭代格式为

由初值起,u1的求解使用Caputo分数阶导数定义,而u2,u3,···,un的求解使用Abdeljawad分数阶导数定义,可得下列近似解

接下来,我们用同伦扰动法求解此问题:
将(3.14)带入(3.13),并比较等式两边p的同次幂得到

用Abdeljawad分数阶积分定义分别对上述方程两边求积分,得
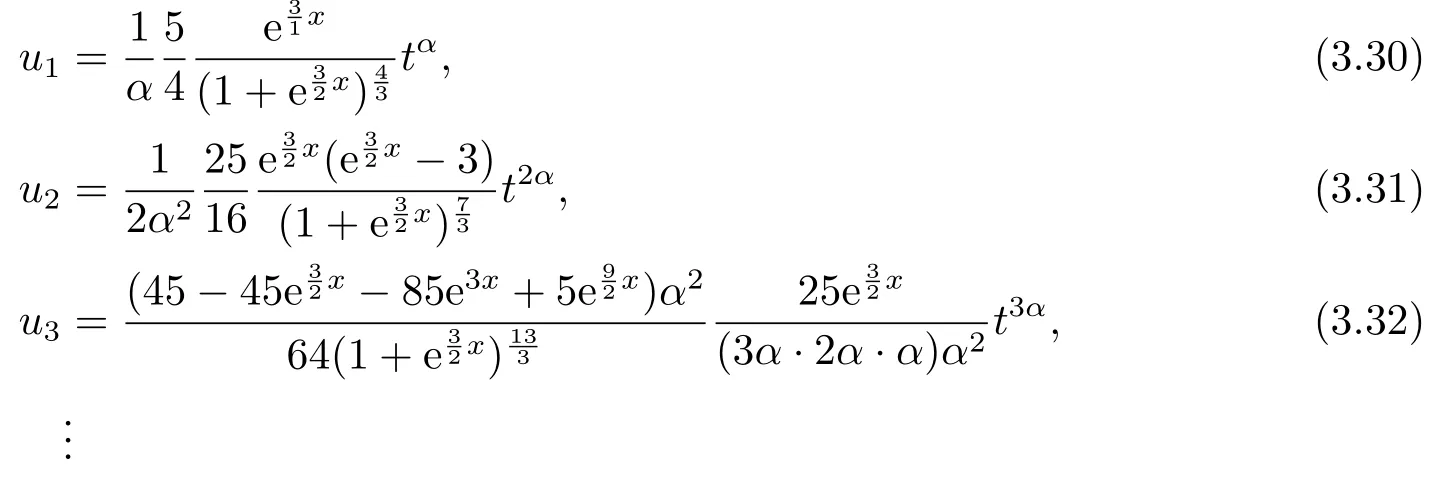
从而,根据同伦扰动法,可得方程(2.20)-(2.21)的级数形式解为:
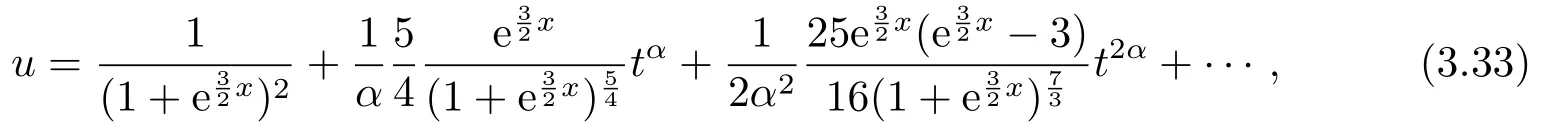
表3.1给出了方程(3.6)当参数时采用分数阶变分迭代法以及同伦扰动法解出的近似解与文献解的对比(取),这里,我们取变分迭代法近似解的第三项,而同伦扰动法,我们取了近似解的前四项,从比较的结果来看两种方法都具有较高的精度,对比结果表明本文所用模型是正确的.

表3.1 方程(3.6)当参数α=1时近似解与文[17]中解的比较
表3.2给出了方程(3.6)当参数α=1,0.6,0.4,t=0.1,0.2,0.4,x=1时采用分数阶变分迭代法和同伦扰动法解出的近似解的对比,这里,我们取变分迭代法近似解的第三项,而同伦扰动法,我们取近似解的前四项,从比较的结果来看两种方法都具有较高的精度,对比结果表明本文所用模型和方法是合理和准确的.

表3.2 方程(3.20)当参数x=1时两种近似解的比较
4.结论
本文利用新的分数解微积分定义结合变分迭代法以及同伦扰动法求解了一类时间分数阶非线性Fisher型扩散方程的近似解,并对得出的模型近似解进行了讨论,最后,与相应的整数阶微分方程的解进行了对比,验证了所用方法求解此类时间非线性分数阶种群扩散方程的准确性.
- 应用数学的其它文章
- A New Class of Estimators for Extreme Value Index
- 一类具记忆项和非线性阻尼项的双曲型方程的整体吸引子
- A Line Search Method with Dwindling Filter Technique for Solving Nonlinear Constrained Optimization
- Martingale Transforms on Variable Exponents Martingale Hardy-Lorentz Spaces
- fmKdV Equation for Solitary Rossby Waves and Its Analytical Solution
- 求解Helmholtz方程的无网格重心插值配点法

