基于极限学习机的板形建模与优化

李滔,廖俊,戴小标，刘志辉

(1.邵阳学院 机械与能源工程学院，湖南 邵阳，422000；2.邵阳学院 高效动力系统智能制造湖南省重点实验室，湖南 邵阳,422000)

随着现代加工技术的发展，许多企业对板材的精度和成本提出越来越高的要求[1]。铝薄板带轧制过程中板形问题主要包括出口横向厚度分布和平直度两个方面[2]。影响板带出口横向厚度分布的因素除轧机刚度、润滑条件、板厚、板宽、轧件横截面厚度是否均匀、原始辊型和轧辊弹性变形等[3-4]外，轧制时的轧制力、弯辊力、张力和喷淋冷却模式的热力耦合作用对板带出口横向厚度分布也产生较大的影响[5-7]。

在板形研究方面，限元法利用非线性接触分析[8]，把工作辊、支撑辊和板带以单元形式划分好，通过单元材料变形和受力分析，单元之间再通过非线性接触传递力和变形，同时，还可以加入温度对单元的膨胀变化量，这样就可以得到最终板带出口单元各节点位移和受力。其计算精度高，还能分析板带温度场分布、残余应力分布、轧制力沿板带方向分布[9]等，但计算时间长，不适合板形的在线预测。分割模型影响函数法也经常应用于板形计算，如利用影响函数分析辊系变形[10-11]。在轧辊弯曲变形量[12]和温度场分析[13]过程中，可以利用差分法建立平衡微分方程与材料塑性变形条件、边界条件之间的关系进行分析。

智能算法在板形研究方面也得到越来越多的应用，如神经网络应用于带钢热连轧过程中的凸度预测[14]研究，利用混沌优化支持向量机方法对板形进行预测[15]，并优化连轧道次中的压下率，建立基于分布式神经网络的板形预测模型[16]等。但传统的BP网络对训练数据的质量和数量有一定的要求，需要消耗大量的时间进行参数调整。对于板带轧制来说，板带越薄，板厚分布和平直度对板形的影响越明显[17]，因此，需要建立反映出口板带厚度横向分布和平直度的板形预测模型。

1 板形缺陷种类和影响因素

板带轧制过程中有许多因素都会引起板形缺陷，它们之间相互影响，共同作用，导致了板带缺陷的产生。轧制出口板带都是某种几何截面形状的来料经轧制作用产生纵向延伸和横向流动，形成最终的出口板带尺寸和形状，轧制过程中的纵向延伸率不同，导致沿板宽方向产生不同的残余应力，最后表现为板形缺陷[18-19]，主要有以下几种表现形式：板带一边延伸率大于另一边，产生单边浪；板宽方向中间延伸率大于两边的延伸率，产生中浪；板宽方向两边延伸率大于中间的延伸率，产生双边浪；此外，还会产生1/4浪和不对称浪。

材料变形性能(如加工硬化、变形抗力等)直接影响轧制过程中轧制力，是与板形密切相关的影响因素，来料几何形状(如来料厚度分布、宽厚比)是影响出口板带形状的另一个重要因素[20]，只有材料具有良好的变形性能和良好的来料几何形状才能保证高精度的板带出口厚度分布。由于轧制条件对板形的影响因素众多，从而显得更为复杂，空载辊缝量、轧辊的材料、直径、初始凸度、热凸度和磨损凸度共同构成了空载辊缝形状，弯辊力也影响辊缝形状，轧制过程中轧制力的分布变化会对辊系整体变形和有载辊缝形状产生较大的影响。

2 板形预测模型的建立

2.1 轧制力对板形影响关系分析

板宽与轧制力对板带厚度分布影响系数Gp的关系。在板厚分布模型中,通过改变板宽单一参数，其他计算参数均不变，计算轧制力对厚度分布影响系数的改变。分别选择板宽为0.6，0.8，1.0，1.2，1.4，1.6和1.8 m这7种不同板宽进行计算。通过这7种不同板宽的计算，把计算结果连接成曲线形式，基本上呈抛物线，因此，可以采用二次函数式来描述，如Gp1B=A1+A2b+A3b2(式中，b为板带宽度，A1和A2为回归系数(以下类同))，采用上述方法可以得到轧辊直径与轧制力对板带厚度分布的影响系数式为

Gp1D=A7+A8Db+A9Dw)。

式中：Db为支撑辊直径；Dw为工作辊直径。

轧制力与轧辊凸度对板厚分布影响系数为

GP1C=a13+a14Cb+a15Cw。

式中：Cb为支撑辊凸度；Cw为工作辊凸度。

前后张力与轧制力影响系数为GP1T=A19Tf+A20Th。

式中：Tf为前张应力；Th为后张应力。

综上分析，可以得到轧制力对板形的影响系数为

Gp1=Gp1BGp1DGp1CGP1T。

2.2 弯辊力对板形影响关系分析

根据前面分析轧制力影响系数转换的思路，同样根据板带宽度、轧辊直径、凸度对弯辊力的影响，最后，得到弯辊力对板形影响系数Gf为

Gf1=[A23+A24b](A25+A26Db+A27)Dw(A28+A29Cb+A30Cw)。

2.3 轧辊凸度和来料凸度对出口板形影响关系分析

由于轧辊在轧制过程中直接与板带接触，板带出口截面形状是由工作辊有载辊缝形状直接决定的，轧辊凸度对出口板带厚度分布的影响与轧辊凸度沿辊身方向分布有关。在分析轧辊凸度分布时，一般选择二次曲线来描述其沿辊身长度方向的分布，因为支撑辊系数Gbr和工作辊系数Gwr为板宽的高次函数系数，所以，它们之间可以用系数乘以板宽与辊身长比值的平方来表示，即

Gwr1=A40(b/Lw)2Cw，Gbr1=A42(b/Lb)2Cb，

其中：b为板的宽度值；Lw为工作辊长度；Lb为支撑辊长度。

通过模型计算在不同板宽下来料凸度对出口板厚分布影响系数的求解，其变化规律同样为沿来料板宽方向呈二次或者高次曲线分布，因此，其与乘以板宽高次项的来料凸度影响系数直接呈线性关系，这样，乘上板宽高次项后影响规律便呈二次曲线规律，同时，入口凸度对出口板厚分布影响系数还与出入口板带厚度之比h/H有关，因此，GCH可以表示为

2.4 厚度分布模型的建立

在板带厚度分布模型研究方面，神经网络建模经常被用来分析对铝精轧板带厚度分布[21]。根据前面分析板形影响因素可以知道，板带厚度分布由轧辊直径、轧制力、弯辊力、板带来料厚度分布、轧辊凸度、以及板带宽度共同作用影响，以四次对称函数式来描述板带厚度分布，得到出口厚度分布关系式为

h(y)=a0+a1x2+a2x4=a0+(GP1P+Gf1Fw+Gwr1Cw+Gbr1Cb+GCH1CH)x2+ (GP2P+Gf2Fw+Gwr2Cw+Gbr2Cb+GCH2CH)x4

(1)

式中:Fw为轧制力大小；a0为中心点板厚值；x为距离板厚中心处的距离。通过各影响系数的转换，可以得到板带板厚分布模型为

h(y)=a0+a1x2+a2x4=a0+(GP1P+Gf1Fw+Gwr1Cw+Gbr1Cb+GCH1CH)x2+ (GP2P+Gf2Fw+Gwr2Cw+Gbr2Cb+GCH2CH)x4

(2)

式中：

其中：A1～A44为回归系数。

在薄板轧制过程中，板带宽展很小，在工程实际计算中可以忽略[22]，再根据体积不变原理，板带横向位移与板带长度比值之和可用压下率表示。根据张应力横向分布[23]

与残余应力分布模型

可以推导出铝薄板带板形平直度计算模型为

(3)

以保证良好平直度要求,对板带截面设置，板带截面就会有一个根据平均压下率计算得到的出口几何曲线形状，那么，th(y)表示为偏离该标准曲线的板厚差值。则有th(y)=h(y)ρ(y)。通过计算得到的平直度分布可以得到板带出口厚度偏离标准曲线的差值分布为

th(y)=ρ(y)×h(y)

(4)

式中：H0表示板带入口设定厚度；h0为出口板带设定厚度。

根据板带出口厚度计算值与标准曲线的偏离值[24-25],可以粗略看出沿板宽方向各点压下率与平均压下率之间的关系，标准值曲线与偏离值曲线对比见图1。

图1 标准值曲线与偏离值曲线对比Fig.1 Comparison of standard curve and deviation value

如果在某点A处，板厚输出值连续一部分值都小于标准曲线计算值，那么可以判断在该处板带将产生一个浪形。通过将平直度转换为厚度分布偏离量，根据式(4)就可得到1个板形预测模型：

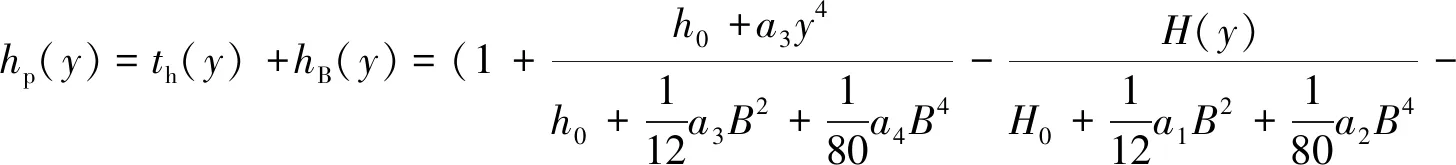
(5)

式中:hp(y)为出口板形预测值；hB(y)为标准曲线上该点厚度；h(y)为板厚回归模型计算值；a1,a2,a3和a4为回归系数；所谓板带截面标准曲线hB(y)就是指本次轧制时，为了与入口板带保持相同的比例凸度所计算得到的出口板带几何形状。

式(5)不仅考虑了板厚分布形状，同时考虑了不同时刻平直度对板形的影响。当用该模型对出口板形预测时联络各个时刻预测值，可以得到板带的各种浪形和板形缺陷。

3 实验数据的采集和回归参数的确定

在4 mm厚铝合金板带轧制生产过程中，在通过4连轧机组最后一道轧机前、后的板厚分布测量仪所测数据中，随机选取250组数据，每组数据包含沿板宽方向的58个实测厚度，采用其中的150组数据，即8 700个实测数据用于回归系数A1～A44的确定。模型中辊系常数参数见表1，把表1中各数代入式(2)中，再采用Marquardt算法[26-27]对式(2)进行回归计算。

表1 辊系常数参数

根据每个测量点的宽度值和每个采样时刻轧制力、入口厚度、入口凸度和板宽等得到A1～A44，再通过各回归系数代入各影响因数可以得到：GP1=3.14×10-6，GP2=6.34×10-6，Gf1=4.051×10-6，Gf2=7.11×10-6，Gwr1=0.304，Gwr2=0.47，Gbr1=0.08，Gbr2=0.132，GCH1=0.21，GCH2=0.57。

4 板形预测

把各回归参数值和第三机架、第四机架轧制参数值代入4个系数a1,a2,a3和a4的求解。然后，把这4个系数代入式(5)即可算得某时刻出口板形预测结果。同时，根据不同时刻的两个机架轧制力、弯辊力、板宽等参数求解不同时刻的系数a1,a2,a3和a4，就可以得到板形随时间的变化情况。

利用剩下的100组采集数据进行计算和对比。如图2所示为100组实测结果，图3所示为式(5)预测模型计算结果。

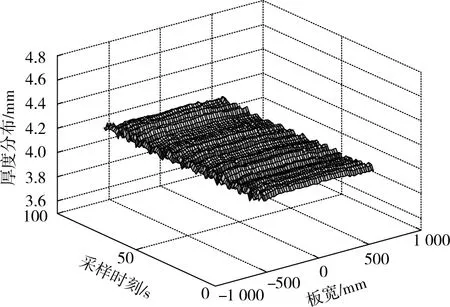
图2 实测板厚值Fig.2 Measured values of strip thickness

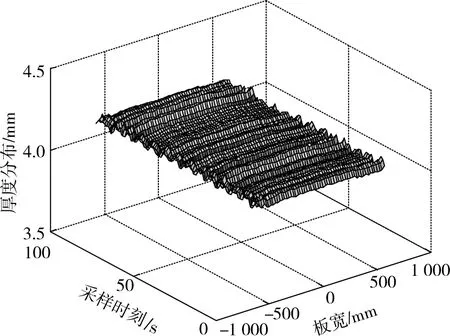
图3 预测模型计算值Fig.3 Calculated values of prediction model

如图4所示为实测板形分布数据与预测模型计算结果误差，从图4中可以看出出误差最大值为0.019 1 mm，最小值为-0.022 3 mm，这就可以看到该板形模型的预测误差范围在-0.022 3～0.019 1 mm。相对误差度见图5，是将图4中各点误差绝对值除以各点的实测厚度再乘以100%得到。

图5中可以找出最大相对误差为0.467%，最小相对误差为-0.544%，可见相对误差值保持在0.544%以内。从图4和图5可以看出：板厚分布预测模型预测误差较小，具有较高的预测精度。

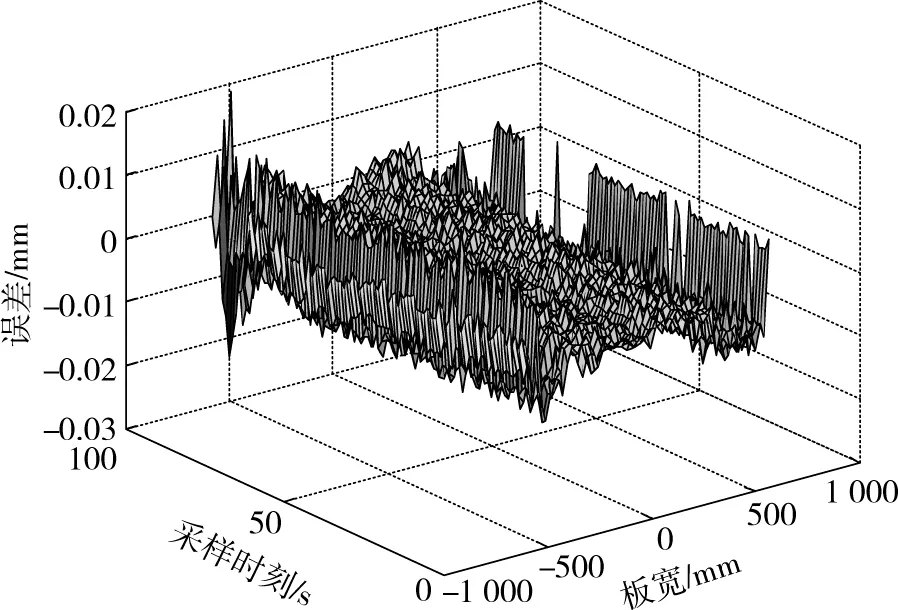
图4 绝对误差值Fig.4 Absolute error traces

图5 相对误差Fig.5 Relative error traces

5 采用极限学习机智能算法进行模型优化

为了进一步提高板形在线预测模型的精度和更好地适应生产过程中未知参数对板形的影响，采用极限学习机[28](extreme learning machine， ELM)对所得预测模型式(5)进行优化。ELM具有简单、易用和有效的特点，只需要对隐层节点个数进行设置，在ELM计算过程中无需对网络的输入权值和隐元的偏置进行调整，都可以通过网络自学习寻找到整体最优解，同时它具有学习速度快且泛化性能好的优点[29]。具体理论[30]如下。

已知训练样本R={(xi,yi)|i=1,2…,N;xi∈Rn;yi∈Rm}，建立含有L个隐层节点的ELM神经网络学习模型：

(6)

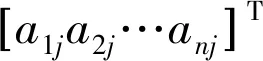
Hβ=Y

(7)

式中：

H为隐含层输出矩阵，在H中当L≤N时，H为列满秩矩阵。为了得到确定的模型解，则必须保证H为列满秩，因此,在对模型进行训练前首先要分析L与N的关系。但在大多数问题中，HUANG等[28]通过分析得到L≤N，也就是说，输出层参数β可以由式(7)的极小2范数最小二乘解得：

β=H+Y

(8)

其中：H+为H的Moore-Penrose广义逆。

式(7)的极小2范数解含有以下特性：

1)可使训练模型输出结果与训练对象值最接近；

2)得到权值的最小范式；

3)只有唯一解。

通过极小2范数的特性可以看出ELM计算方法具有许多优点：一是模型训练中可以任意设置输入层数，它都能通过Moore-Penrose广义逆求解出输出层权值；二是它具有极端快速的特点，因为它只需要对隐层神经元结点数进行学习和调整，且在学习调整过程中一步到位，不需要进行多次迭代；三是它还具有较强的泛化能力，可以更好地被应用于不同领域的不同问题。

以ELM的学习算法建立的模型在计算过程中简单明了，具体计算过程如下：

1)随机设置输入权值aj以及偏置bj，j=1,…,N。

2)计算隐层输出矩阵H。

3)计算输出权值β：β=H+Y,式中Y=[y1,y2,…,yn]T。

通过ELM的计算过程分析，不难看出ELM与传统的单隐层神经网络计算方法相比具有较多优势。在模型的训练过程中可自动对w和b进行调节调整，无需人为输入和调节，只需要对β进行设置，通过一个输出层参数的调节就可以得到训练后的唯一最优解。其计算过程大大简化，在参数选择上面就比其他神经网络算法简单，所以，训练速度得到较大提高，且在计算全局最优解过程中不会陷入局部最优。

为了更好地进行比较分析，模型训练过程采用上述150组回归计算数据，训练完以后通过极限学习机建立1个隐式的参数修正关系式，然后，利用该关系式对修正参数进行计算，最后，把计算所得值加入预测模型中。在ELM修正模型训练过程中，选择影响板厚分布的9个输入参数作为训练参数。根据式(5)所得修正参数预测模型计算结果见图6。利用极限学习机所得修正参数的板厚分布预测模型计算结果与实测值对比见图7，其中最大值为0.014 1 mm，最小值为-0.016 0 mm，可以看出误差范围控制在-0.016 0～0.014 1 mm，修正后的模型预测误差明显比修正前小。极限学习机修正参数模型计算值与实测值之间的相对误差见图8，其中最大相对误差为0.342 6%，最小相对误差为-0.41%，可以看出板厚分布相对误差绝对值控制在0.41%以内，修正后的板厚分布预测模型可以达到较高的预测精度值。板厚分布预测模型修正后计算误差与修正前计算误差对比见表2。从表2中可以看出采用极限学习机修正后，模型预测误差范围明显比修正前小，误差范围缩小27%，从而说明智能算法对预测模型的修正是有效的，修正后的相对误差绝对值小于0.41%。

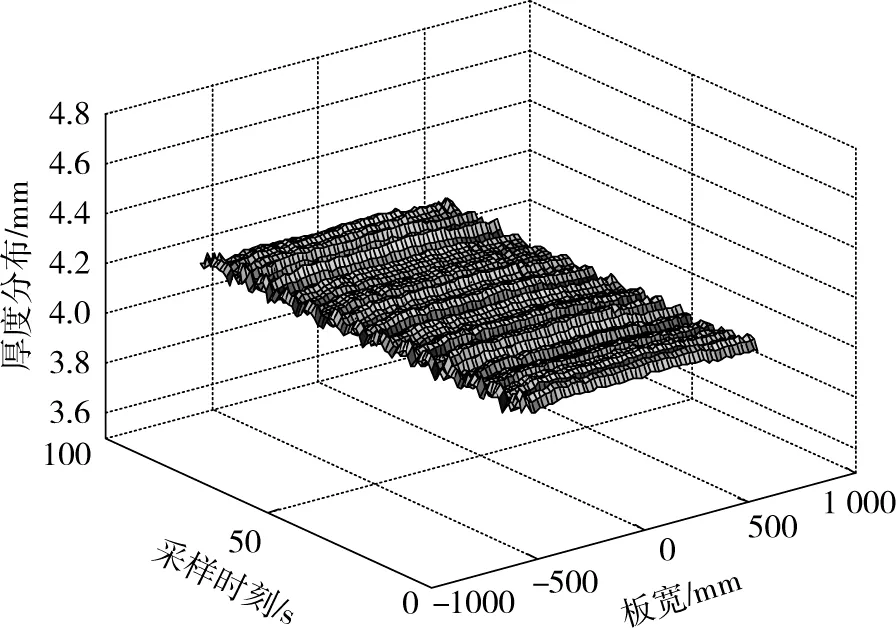
图6 修正参数板形预测结果Fig.6 Strip shape prediction results after specification corrected

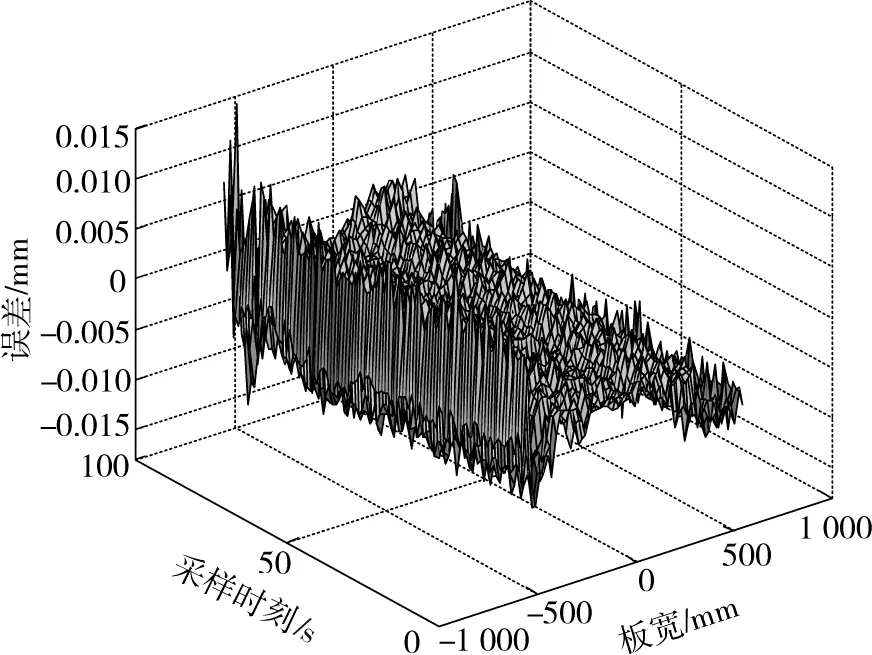
图7 修正模型计算值与实测值对比Fig.7 Comparison of calculated values for the corrected model and measured values

图8 修正模型回归误差Fig.8 Regression error for the corrected model

表2 模型修正前后误差对比

6 结论

1)通过平直度与板厚分布的转换关系，以平直度与相对标准截面曲线差值来判断板形中的各种浪形，建立了一个新的板形预测模型，并通过板带轧制过程中实测数据对预测模型进行验证分析。2)计算结果表明，该预测模型计算值与实测值相对误差保持在0.544%以内。同时，为了克服预测模型中的不足和进一步提高预测板形精度，通过对不同神经网络算法的对比分析，选择了收敛速度快并预测精度较高的极限学习机单隐层神经网络算法，对铝合金薄板带轧制过程中板形预测模型进行修正。在系数修正模型中，对修正系数进行了训练回归，通过修正参数预测模型计算值和实测值比较，最终修正后的模型预测相对误差达在0.41%以内，提高了预测模型的预测精度。