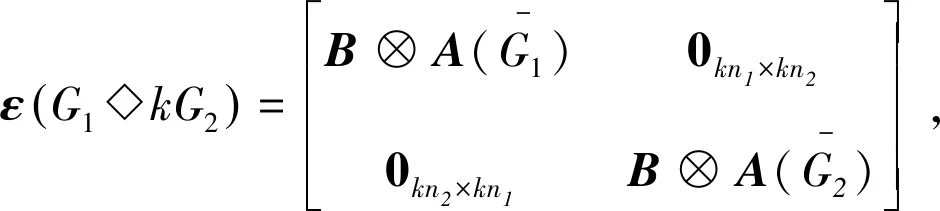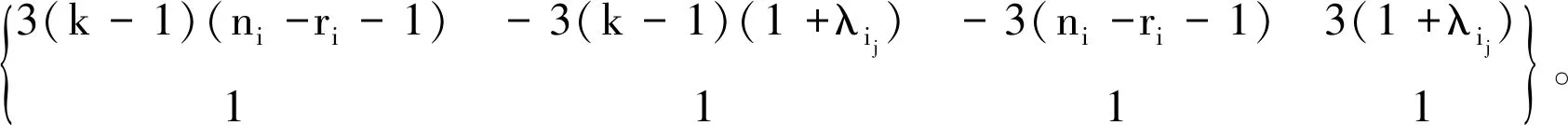关于图运算的离心矩阵的谱

邱正萍，洪文豪，汤自凯

(湖南师范大学 数学与统计学院，湖南 长沙，410081)

连通图G如图 1所示，图G的距离矩阵D(G)与离心矩阵ε(G)分别如下：

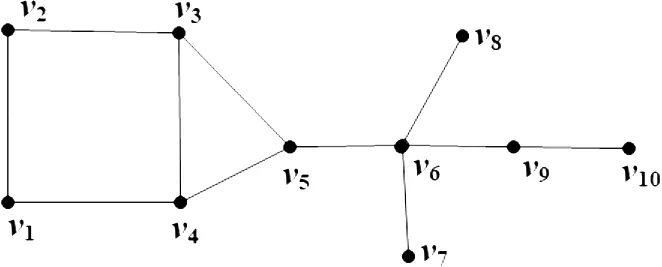
图1 连通图GFig.1 A connected graph G

由于离心矩阵ε(G)是对称矩阵，因此,图G的离心矩阵的特征值为实数。设ε1>ε2>…>εt为图G离心矩阵各不相同的特征值，则图G的离心矩阵的谱Specε(G)可写为

其中：ni表示特征值εi的重数(1≤i≤t)[4]。

文献[1-4，8-13]研究了图的离心矩阵及其谱的有关性质，如图连通性与图离心矩阵的不可约性、离心矩阵与邻接矩阵的特征值之间的联系、离心矩阵的谱半径的上下界等。文献[3]给出了冠图Kn°G、轮图Wn,Cocktail-party图CP(n)，完全k部图等的离心矩阵的谱，棒棒糖图Lm，n和路Pn相应离心矩阵的不变量(正负惯性指数)等。

本文主要研究图运算的离心矩阵的谱，给出了冠图(Cn°Pm,Cn°Cm),(n，1)-杠铃图Bn，1和2个双重积图(G1■kG2，G1◇kG2)的离心矩阵的谱具体计算公式等。

1 预备知识

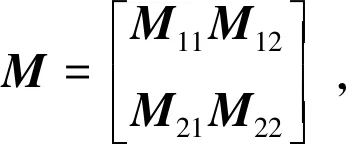
引理3[3]设矩阵A∈Rn×n、B∈Rm×m，矩阵A的谱为Spec(A)={λ1，λ2，…，λn}，矩阵B的谱为Spec(B)={μ1，μ2，…，μm}，则Spec(A⊗B)={λiμj∶i=1，2，…，n；j=1，2，…，m}。

2 主要结论

先给出一个重要的引理。

证明由Schur补集公式和引理2，可得矩阵M的特征多项式为

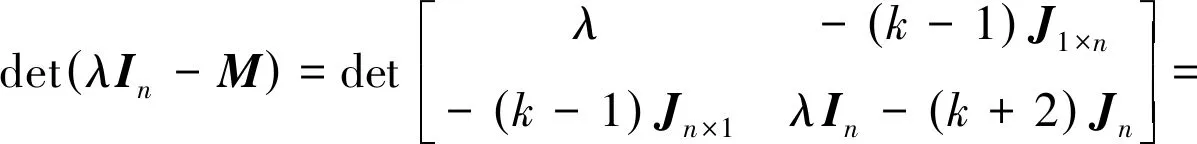
设圈Cn的顶点集V(Cn)={v1，v2，…，vn}，图G的顶点集的顶点集V(G)={u1，u2，…，um}，对图G复制n次后所得图记作Gi(1≤i≤n);设图Gi的顶点集的顶点集V(Gi)={ui1，ui2，…，uim}，将图Gi的每一个顶点同圈上的顶点vi相连后得到的图定义为圈Cn与图G的冠图Cn°G。 下面给出冠图Cn°G(G是连通图)的离心矩阵谱的计算公式。

定理1 假设Cn与Pm分别是n阶的圈、长度为m-1的路。

1)当n=2k时，有

2)当n=2k+1时，有

证明假设圈的顶点集为V(Cn)={v1，v2，…，vn}，路的顶点集为V(Pm)={u1，u2，…，um}，令i=1，2，…，n;j=1，2，…，m，将路Pm复制n次记作Pmi，其顶点集记为V(Pmi)={ui1，ui2，…，uim}，令Vj={u1j，u2j，…，unj}，那么冠图Cn°Pm的顶点集为{V(Cn)，V1，V2，…，Vm}。对冠图的顶点进行适当的排序后可得Cn°Pm,有如下形式的距离矩阵:

其中:J是n阶的全1矩阵;D是圈Cn的距离矩阵;I是n阶的单位矩阵。

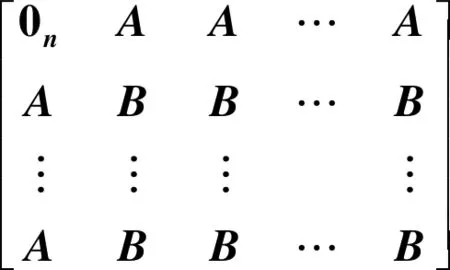
其中：

从而，根据引理3可以得到，ε(C2k°Pm)的谱为

2)当n=2k+1时，根据冠图C2k+1°Pm的距离矩阵可得离心矩阵为

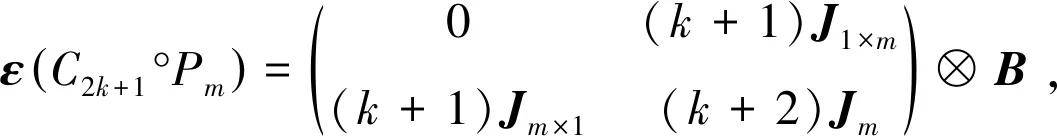
故由引理3可知,离心矩阵ε(C2k+1°Pm)的谱为

i=1，2，…，2k+1。

定理2 假设Cn与Cm是长度分别为n和m的圈。

1)当n=2k时，有

2)当n=2k+1时，有

。

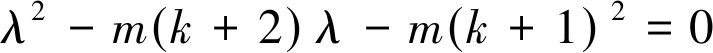
证明假设圈Cn的顶点集为V(Cn)={v1，v2，…，vn}，圈Cm的顶点集为V(Cm)={u1，u2，…，um}，令i=1，2，…，n;j=1，2，…，m。将圈Cm复制n次记作Cmi，其顶点集记为V(Cmi)={ui1，ui2，…，uim}，令Vj={u1j，u2j，…，unj}，那么，冠图Cn°Cm的顶点集为{V(Cn)，V1，V2，…，Vm}。对冠图的顶点进行适当的排序后可得，Cn°Cm有如下形式的距离矩阵：

其中：J是n阶的全1矩阵；D是圈Cn的距离矩阵；I是n阶的单位矩阵。显然，由距离矩阵可知离心率矩阵ε(Cn°Cm)=ε(Cn°Pm)，从而Specε(Cn°Pm)=Specε(Cn°Cm)。

由定理1与定理2得推论1。

推论1 冠图Cn°Pm和Cn°Cm共谱。

设G是具有n个顶点的简单无向的连通图，对图G复制两次记为G1，G2，另取一个孤立顶点u∉V(G)并与G1，G2中的每一个顶点相连，所得的图称为(n，1)-杠铃图，记作Bn，1。

定理3 假设图G是具有n个顶点的r-正则图并且Bn，1是(n，1)-杠铃图，图G的邻接矩阵A(G)的特征值假设为r=λ1>λ2≥λ3≥…≥λn，那么图Bn，1离心矩阵的谱为

其中：t1和t2是方程t2-2(2n-r-1)t-2n=0的2个根。

证明设图G是具有n个顶点的r-正则图，对图G复制得到图G′，将孤立点u∉V(G)∪V(G′)与G′，G中的每一个顶点相连，得到(n，1)-杠铃图Bn，1，令r=λ1>λ2≥λ3≥…≥λn为图G的邻接矩阵A(G)的特征值。由图Bn，1的结构易得其离心率矩阵为

因为ε(Bn，1)的特征多项式为

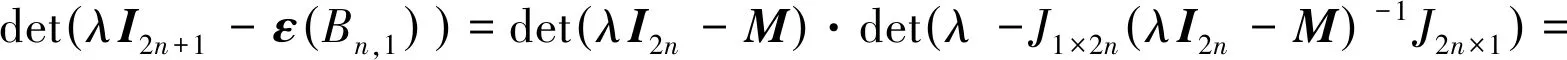
设图G1与G2是连通图，记G1i=G1，G2i=G2(1 ≤i≤k)，表示对图G1与G2复制后所得的图。第一种积图运算，首先，做k次的联图G1i∨G2i(i=1，2，…，k)；其次，将图G2m与G2n中复制时相对应的顶点连以边，其中，1≤m，n≤k且m≠n，所得的新图记作G1■kG2[12,14]。第二种积图运算，首先，做k次的联图G1i∨G2i(i=1，2，…，k)；其次，将图G2m与G2n中复制时相对应的顶点连以边以及将图G1m与G1n中复制时相对应的顶点连以边，其中，1≤m，n≤k且m≠n，所得的新图记作G1◇kG2[12,14],见图 2。

图2 两类积图P2■3P3与P2◇3P3Fig.2 Two product graphsP3■3P3 and P2◇3P3

定理4设图Gi是具有ni个顶点的ri-正则图(i=1，2)，r2=λ1>λ2≥λ3≥…≥λn2为图G2的邻接矩阵A(G2)的特征值，则图G1■kG2离心矩阵的谱为

其中：i=2，3，…，n2。

证明由文献[12]的描述可知图G1■kG2的距离矩阵如下：

其中：J为全1矩阵；A1=2(J-I)-A(G1)；A2=2(J-I)-A(G2)；A3=3J-2I-A(G2)。

因为图G1■kG2中每一点的离心率为3，从而得图G1■kG2的离心率矩阵：

定理5令i=1，2，j=2，3，…，ni，假设图Gi是具有ni个顶点的ri-正则图，ri=λi1>λi2≥λi3≥…≥λini是图Gi的邻接矩阵A(Gi)的特征值，则图G1◇kG2的离心矩阵的谱为

证明由文献[12]的描述可知图G1◇kG2的距离矩阵如下：

其中：J为全1矩阵;A1=2(J-I)-A(G1);A2=2(J-I)-A(G2);A3=3J-2I-A(G2);A4=3J-2I-A(G1)。