具有最大度的图增强型Zagreb指数的上界

周后卿,姚志雄

(1.邵阳学院 理学院，湖南 邵阳，422000；2.邵阳市第一中学，湖南 邵阳，422000)

图的拓扑指数是一个可以用来描述分子图的某些性质的不变数值量，拓扑指数可以分为几个不同的组，用分子图代表碳氢化合物有机分子的碳原子骨架，作为分子结构描述符在化学领域得到了广泛应用[1-3]。近几十年来，对图的拓扑指数研究取得了丰硕成果，这些研究成果对定量结构-活性/性质关系(quantitative structure-activity/property relationship，简写成QSAR/QSPR)的研究以及生物和化学化合物的结构性质研究都有一定的参考价值。Zagreb指数是化学图论中的一个重要拓扑指数，关于Zagreb指数有许多研究成果，参见文献[4-9]。基于顶点度的指数是研究较多和应用较广泛的一类指数,仅仅依赖于分子图的顶点度。1998年，ESTRADA等[10]提出了原子键连通性(atom-bond connectivity)指数(简称ABC指数)，定义为

该指数为直链烷烃和支链烷烃的稳定性以及环烷烃的应变能提供了良好的模型,关于该指数的研究结果见文献[11-14]。受ABC指数的启发，FURTULA等[12]提出了ABC指数的修改版本，称为增强型Zagreb指数(augmented Zagreb index, 简记作AZI)。

在研究庚烷和辛烷的生成热时，增强型Zagreb指数(AZI)预测能力强于ABC指数[15]。

设G=(V,E)是具有n个顶点、m条边的简单连通图，图G的顶点集记作V={v1,v2,…,vn},图G的边集用E表示。顶点vi的度记作di。设图G的度序列为{d1,d2,…,dn}，最大度记作Δ。那么，定义图G的第一类Zagreb 指数和第二类Zagreb指数分别为

人们对增强型指数进行了研究，获得了一些有价值的结论[15-22]。特别是文献[23]刻画了所有顶点固定的C-圈图中具有最小增强型Zagreb指数的唯一图的特征。

本文讨论具有最大度的任意图的增强型Zagreb 指数的界问题。

1 有关增强型Zagreb指数的几个结论

首先看几个关于增强型Zagreb指数的结果。FURTULA等[15]给出了顶点n(n≥3)的化学树(所谓化学树，是指每一个顶点的度不超过4的树，用来表示碳原子的烷烃骨架图)的AZI的界。

设G是顶点为n的化学树，则G的AZI满足下列不等式：

。

并且证明了在所有树中，星图的AZI指数最小。

对于化学双圈图Bn(指没有顶点大于4度的图)，文献[16]获得了下列结果：

并且还得到了化学单圈图Un的AZI的界:

文献[19]利用边数最大最小度，给出了AZI(G) 的范围。证明了若G是1个边为m(m≥2) 的连通图，最大度为Δ，最小度为δ，则

左边式子成立，当且仅当δ>2时，G是1个δ-正则图，要么当δ=2时，G的每条边至少有1个2度的端点；右边式子成立当且仅当G为路或Δ-正则图。

文献[20]利用图的边数、悬挂点数、最大度以及非悬挂点的最小度等参数，给出了AZI(G)一个下界。证明了若G是具有顶点n≥3、边m、悬挂点p、最大度Δ的简单连通图，假设δ1是G的非悬挂点的最小度，则

式子成立当且仅当G是正则图或G有度集合{1，Δ}；或G是每条悬挂边都与1个度Δ的顶点相关联的图，且每一条非悬挂边至少有1个2度的端点；或者G是最小度为2的图，且每条边至少有1个2度的端点。

文献[21]证明了只需知道图的边和最大度数，就能给出AZI(G)一个下界。若G是一个边为m(m≥2) 的简单连通图，最大度为Δ，则

式子成立当且仅当G是1个星图。

文献[22]在文献[21]的基础上，对其结论进行了改正，得到了结论：若G是1个顶点为n(n≥3) 、边为m、最大度为Δ的简单连通图，则

式子成立当且仅当G是1个完全图。

文献[23]在文献[22]的基础上又进一步证明，若G是1个顶点为n(n≥3) 、边为m、最大度为Δ的简单连通图，则

式子成立当且仅当G是1个正则图。

2 主要结论

为了获得本文的结论，需要下列引理1。

引理1[24]若图G=(V,E)是具有顶点n的简单图，则

首先证明定理1。

定理1 若图G是具有顶点n(n≥3)、边为m的简单连通图, 则一定存在某个正数α(0<α≤1),使得下式成立：

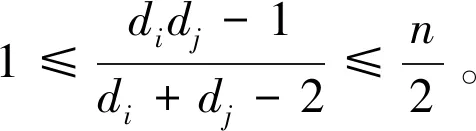
从而

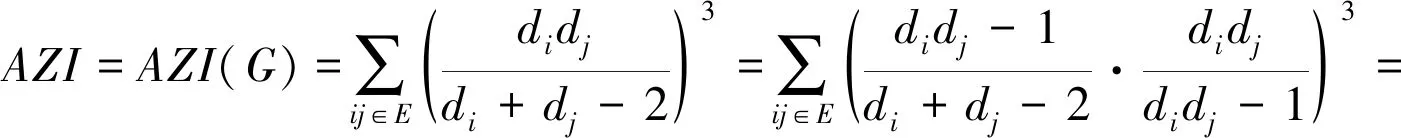
于是，命题得证。

定理2 若图G是具有顶点n(n≥3)、边m最大度为Δ的简单连通图，则

证明当n=3时，图G只有2种情形，见图1。

(a) 具有3个顶点的树；(b)具有3 个顶点的完全图图1 具有3个顶点的树及其完全图Fig.1 A tree with 3 vertices and a complete graph on 3 vertices

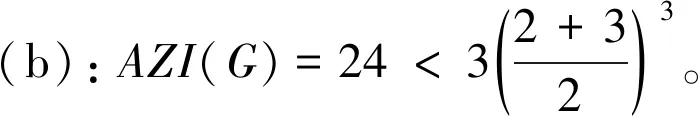
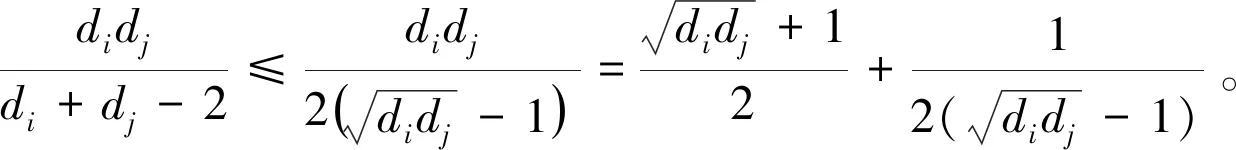
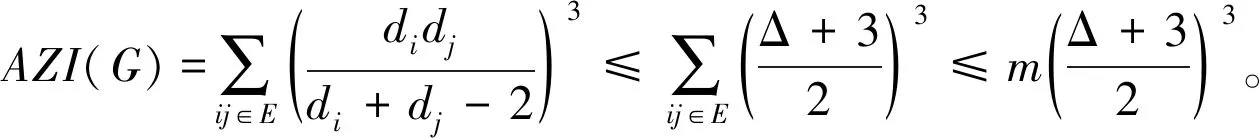
因此，定理2得到证明。