非线性分数阶微分方程的新迭代法

张亚平

(邵阳学院 理学院，湖南 邵阳，422000)

分数微积分理论是研究任意阶微分和积分的数学性质和应用的一种理论。分数阶微积分算子具有非局部性，非常适用于描述现实生活中具有记忆以及遗传性质的材料[1-4]。1926年，Richardson发表了关于湍流扩散的论文,反常扩散被世人所关注。在许多复杂的系统里，扩散过程不再呈现高斯分布，相应的第二定律也不能描述相关的传输行为，而次扩散运动在反常碎片形几何上的传输、多孔渗水系统等问题中都特别重要[5]。然而，分数阶微分方程的解析解都含有复杂的特殊函数，且很多方程无法得到解析解，故研究分数阶微分方程的数值解很有必要。分数阶微分方程的数值解法和经典微分方程的解法很相似。有限差分法的优点是格式构造简单[6-7]；有限元法能适应复杂的求解区域[8-9];谱方法，包括拟谱方法、谱配置法、谱tau和谱Galerkin方法等[10-12]；另外，还有BHALEKAR等[13-14]提出的新迭代方法(NIM)、变分迭代法(VIM)和Adomian分解方法(ADM)[15]等。本文运用NIM，在文献[16]的基础上进行进一步研究。下面分别介绍NIM在非线性反常次扩散方程(NA-SubDE)和非线性时空分数阶反应-扩散方程(NTSFRDE)中的应用。

1 预备知识

考虑下面一般的函数方程：

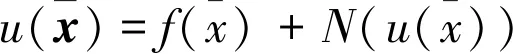
(1)

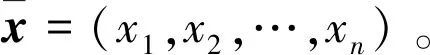
(2)

非线性算子N分解为

(3)

定义递推关系：

(4)

得到式(1)和(2)的k项近似解为u=u0+u1+…+uk-1。

2 非线性反常次扩散方程[17]

2.1 NA-SubDE的迭代格式

(5)

u(x,0)=p(x)

(6)

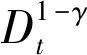
(7)

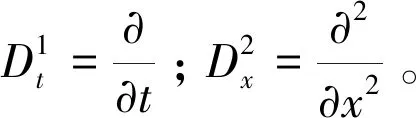
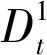
(8)

假设

再由非线性算子N分解式(3)得到式(7)的等价形式为

(9)

由递推关系式(4)得到

u1+…+um+1=N(u0+…+um)；m=1,2，…,

和

式(7)的k项近似解为u=u0+u1+…+uk-1，增加分解序列的项能减少总体误差。

2.2 数值试验

考虑非线性反常次扩散方程初值问题：

(10)

u(x,0)=p(x)=0

(11)

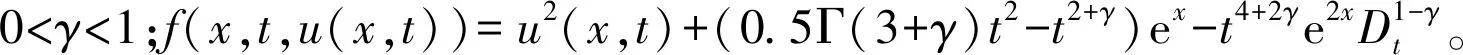
当γ=0.9时，可得

u0+u1=(t2.9-0.073 066 353t4.7)ex+(0.203 924 591t5.8-0.179 291 152t6.7- 0.210 070 123t7.6+0.012 792 179t8.5-0.172 065 523t10.5)e2x+ 0.047 487 408t11.4e3x+0.046 779 543t14.3e4x。

当γ=0.9,t=0.5时，由新迭代方法得到的前两项的近似解、Adomian分解方法得到的前3项的近似解、非线性反常次扩散方程的精确解的比较，见表1。

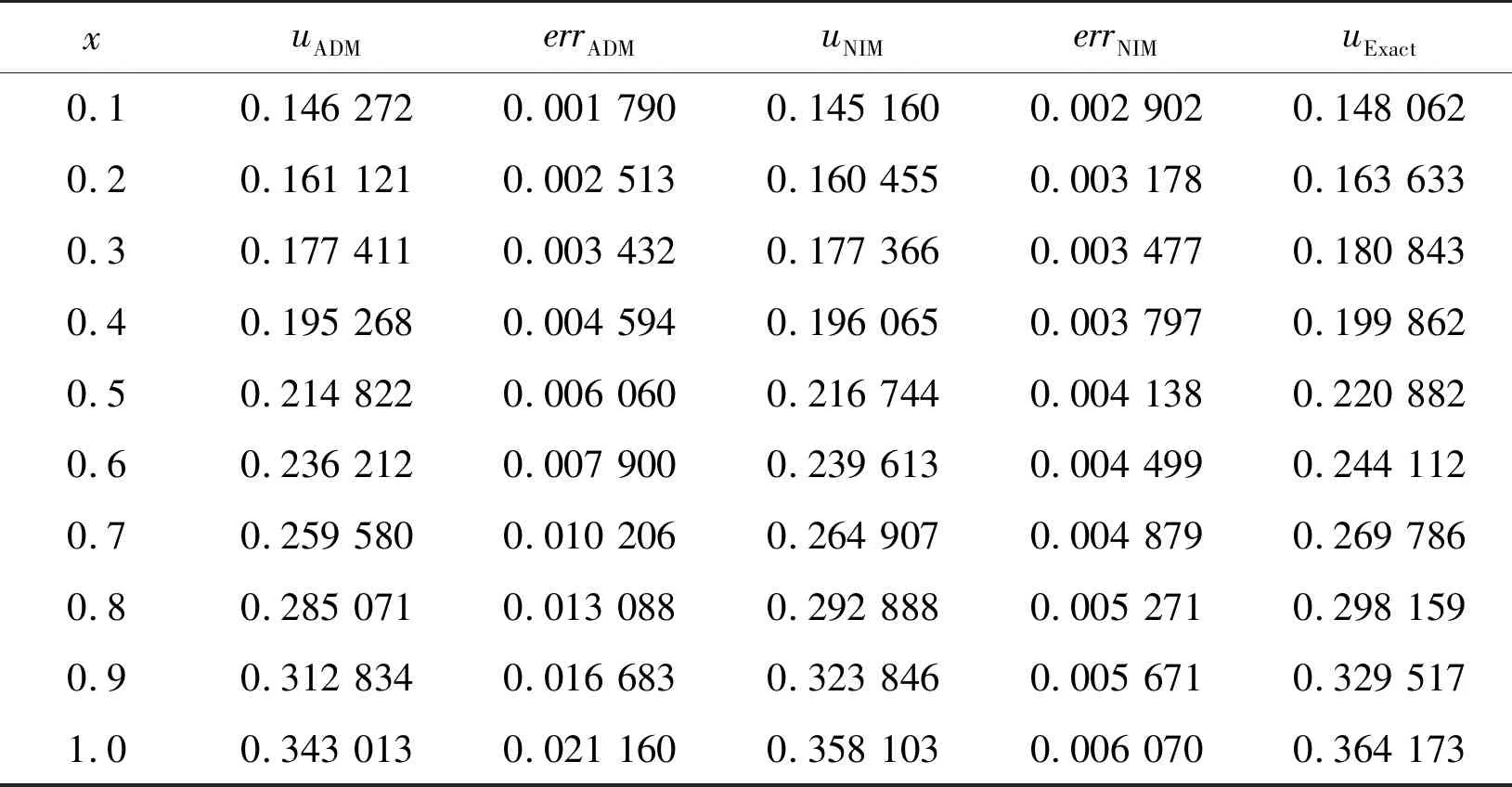
表1 ADM方法、NIM方法数值解和误差的比较

表1表明，NIM和ADM相比较，NIM精确度更高，与精确解的逼近更好。

3 非线性时空分数阶反应-扩散方程[18]

3.1 NSTFRDE的算子形式为

(12)

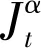
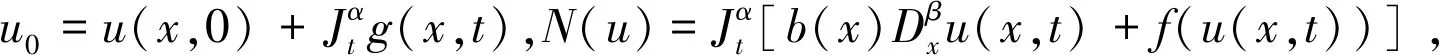
3.2 数值试验

下面以时间分数阶偏微分方程为例进行数值验证。

(13)

u(x,0)=0。

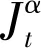
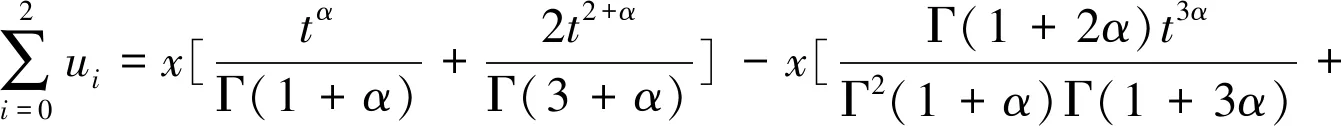
当α=1.0时，式(13)的真解为u(x,t)=xt,ODIBAT等[15]分别用变分迭代方法(VIM)和Adomian方法(ADM)得到式(13)的数值解。从计算量考虑，VIM无需求ADM中的Adomian多项式，只要利用初始条件和迭代公式就能得到近似解，与NIM计算量相当，但是NIM的精度更高。在α=1.0时，比较ADM，VIM和NIM数值解和精确解可知，NIM更逼近真解，见表2。这3种方法在α=0.5和α=0.75时的数值结果见表3。

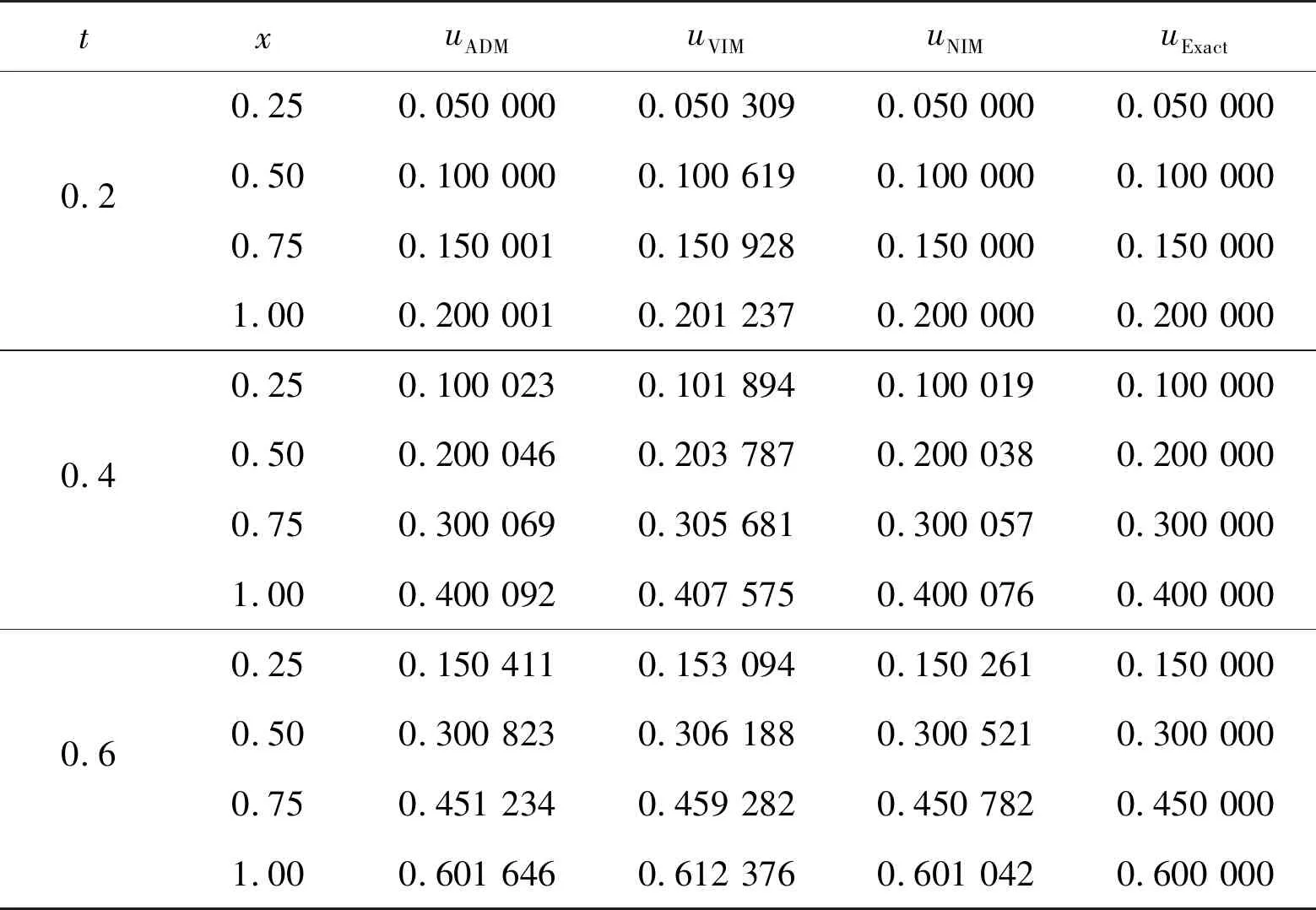
表2 不同方法的数值解与精确解的比较(α=1.0)

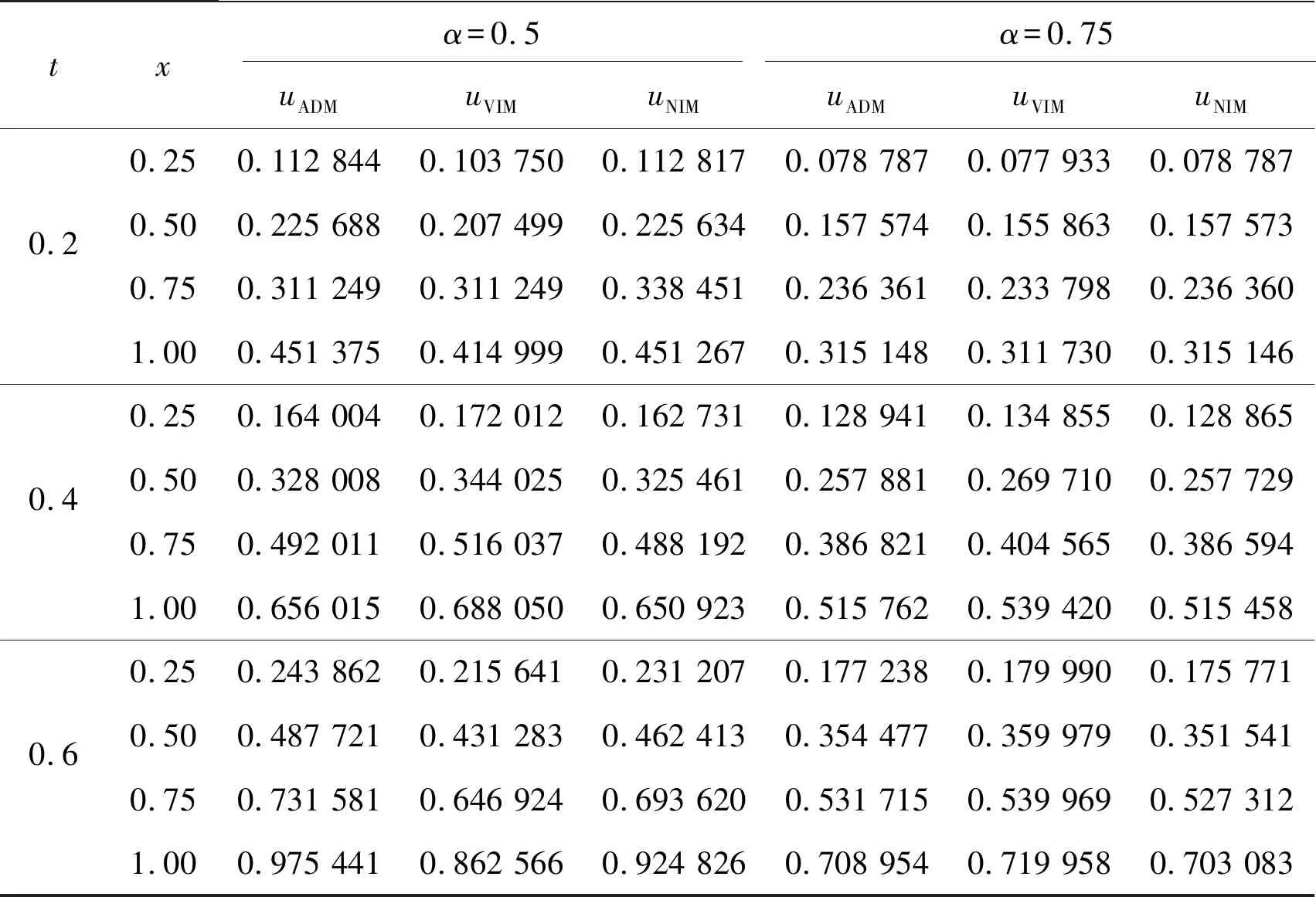
表3 ADM，VIM，NIM数值解的比较(α=0.5，0.75)

4 结论

本文讨论了NIM在非线性反常次扩散方程和非线性时空分数阶反应-扩散方程中的应用，给出方程级数形式的解，此方法很好的处理了非线性反应项，且相比于ADM，得到更高精度的近似解，从数值上验证了方法的有效性。