钢框架内填再生混凝土墙结构等效模型分析
孙立建,郭宏超,刘云贺,刘 杰
(西安理工大学土木建筑工程学院,陕西西安710048)
钢框架内填钢筋混凝土剪力墙结构因具有抗侧刚度大,水平承载力高的优点,近年来得到广泛研究,并逐步应用于工程实际[1]。随着对再生混凝土研究的深入,文献[2]认为再生混凝土剪力墙可以用于有抗震设防要求的地区。文献[3]将再生混凝土墙板用于钢框架结构中,通过对钢框架内填再生混凝土墙结构的试验研究发现:内填再生混凝土墙结构的承载力、抗侧刚度、延性、耗能能力等与内填普通混凝土墙结构相差不多,内填再生混凝土墙结构具有较好的滞回性能。文献[4-5]对钢框架内填钢筋混凝土剪力墙结构复杂的破坏机理进行了分析,并提出了基于塑性理论的侧向承载力简化计算方法。文献[6]通过借鉴钢板剪力墙的拉杆模型,提出了钢框架内填钢筋混凝土剪力墙结构等效斜压板带模型,来反映在地震荷载作用下该结构的传力机理,对混凝土填充墙体的力学简化分析具有重要意义。
本文以文献[3]中的试验模型及研究成果为基础,通过对钢框架内填再生混凝土墙结构在柱顶水平荷载作用下的受力性能进行分析,基于再生混凝土墙的裂缝分布及受力特点,将内填墙板离散成一系列等宽度的斜压板带,即等效斜向板带模型,并根据各板带传递荷载的大小,对斜压板带的有效宽度进行了调整。利用有限元程序ABAQUS对钢框架内填再生混凝土墙结构整体模型进行了分析,在验证有限元分析方法可行的基础上,又通过对不同板带数量斜向板带模型的分析,及不同高跨比、内填墙板厚度和混凝土强度的参数扩展分析,确定了钢框架内填再生混凝土墙结构斜向板带模型板带数的合理取值,及板带数量对斜向板带模型荷载-位移曲线的影响。
1 试验概况
试验模型为单层单跨1:3缩尺的钢框架内填再生混凝土墙结构,试件详细构造见文献[3]。其中,试件高度为1 200 mm,跨度1 050 mm;钢框架梁柱采用栓焊混合连接节点,梁截面为HN150×100×5×8,柱截面为HM150×150×7×10,连接螺栓为4根10.9级M16高强螺栓,钢材型号均为Q235B。内填墙板为再生粗骨料取代率100%的再生混凝土墙,混凝土设计强度C30,墙板宽、高、厚分别为900 mm、1 125 mm、90 mm,墙板内布置双层双向Φ6钢筋网,间距为120 mm,在墙板四周设置暗梁、暗柱,暗梁、暗柱内配置4根Φ8钢筋,箍筋为Φ6钢筋,间距50 mm,钢筋型号均为HPB300,墙板配筋见文献[3];钢框架与内填墙板的连接件为沿钢框架内翼缘设置的M16抗剪栓钉,间距为110 mm。
2 等效模型
2.1 受力分析
在柱顶水平荷载作用下,钢框架内填再生混凝土墙结构受力分析见图1,图中A、B、C、D为钢框架对角线编号。

图1 内填墙板受力分析Fig.1 Force analysis of infilled wall
当正向加载时,钢框架沿对角线AC缩短对内填墙板产生挤压作用,沿对角线BD伸长对内填墙板产生拉伸作用,即内填墙板沿对角线AC传递压力,沿对角线BD传递拉力;反向加载时,受力情况刚好相反。因再生混凝土的抗拉强度远小于其抗压强度,当内填墙板的主拉应力大于再生混凝土的抗拉强度时,将沿内填墙板主压应力方向产生剪切斜裂缝。随着水平荷载的增加,斜裂缝不断扩展直至沿整个墙面贯通,内填墙板被分割成一系列斜向板带,水平剪力经由斜向板带主要以压力的形式传递。
钢框架内填再生混凝土墙结构内填墙板的裂缝分布见图2。由图2及试验分析可知,内填墙板对角斜向板带传递大部分水平剪力,而远离对角线的斜向板带传递的水平剪力较少。

图2 内填墙板裂缝分布Fig.2 Cracks distribution of infilled wall
2.2 斜向板带模型
在明确钢框架内填再生混凝土墙结构受力特点的基础上,对其进行等效模型简化。首先把内填墙板分割成一系列等宽度的对称斜向板带,见图3。图3中,h为内填墙板高度,l为内填墙板宽度,xi为每条斜向板带的水平向坐标,yi为每条斜向板带的竖向坐标,S为板带宽度,θ为板带倾角,ns为板带数。

图3 斜向板带示意Fig.3 Sketch of diagonal strip
由图3可知:
(ns+1)·S=l·sinθ+h·cosθ
(1)
为了反映内填墙板靠近对角线的斜向板带传递大部分水平力,远离对角线的斜向板带传递小部分水平力的传力特点,需引入有效宽度系数η来对斜向板带的有效宽度进行调整。斜向板带有效宽度调整的思路为:靠近对角线的板带宽度最大,称为主对角板带,传递大部分水平力;远离对角线的板带宽度逐渐减小,称为次对角板带,传递的水平剪力也相应减少。
板带倾角的取值:①根据文献[6]的研究成果可知,斜向板带倾角θ取40°~50°之间时可较好地描述内填墙板的性能;②由文献[7-9]的试验现象可知,不同高跨比试件的內填混凝土墙板的裂缝均大致沿45°方向发展;③本文內填墙板的裂缝多数沿墙板对角线方向发展,少数大致沿45°方向,且本文试件高跨比略大于1,即对角线方向与水平向的夹角略大于45°。综合考虑,本文板带倾角θ取45°。
在正向加载时,-45°方向的板带承受压力,传递大部分水平剪力,45°方向的板带承受拉力,因混凝土的抗拉强度较小,传递的水平剪力较少;反向加载时,受力情况刚好相反。为了对斜向板带模型进一步简化,提出如下假定:①斜向板带只传递轴向荷载,因此斜向板带两端与钢框架的连接简化为铰接;②为保证主对角板带传递大部分水平剪力,主对角板带的一端与梁柱节点相交。简化斜向板带模型见图4。

图4 简化斜向板带模型Fig.4 Simplified diagonal strip model
2.3 模型参数计算
斜向板带模型板带数较少时,不能较好地反映内填墙板的性能,板带数较多时,又会使分析过程变得复杂,因此本文板带数ns取值为4~9,以确定板带数的合理取值及板带数量对斜向板带模型荷载-位移曲线的影响。斜向板带厚度与内填墙板相同,模型其他参数见表1~2。

表1 板带宽度参数Tab.1 Parameters of strip width
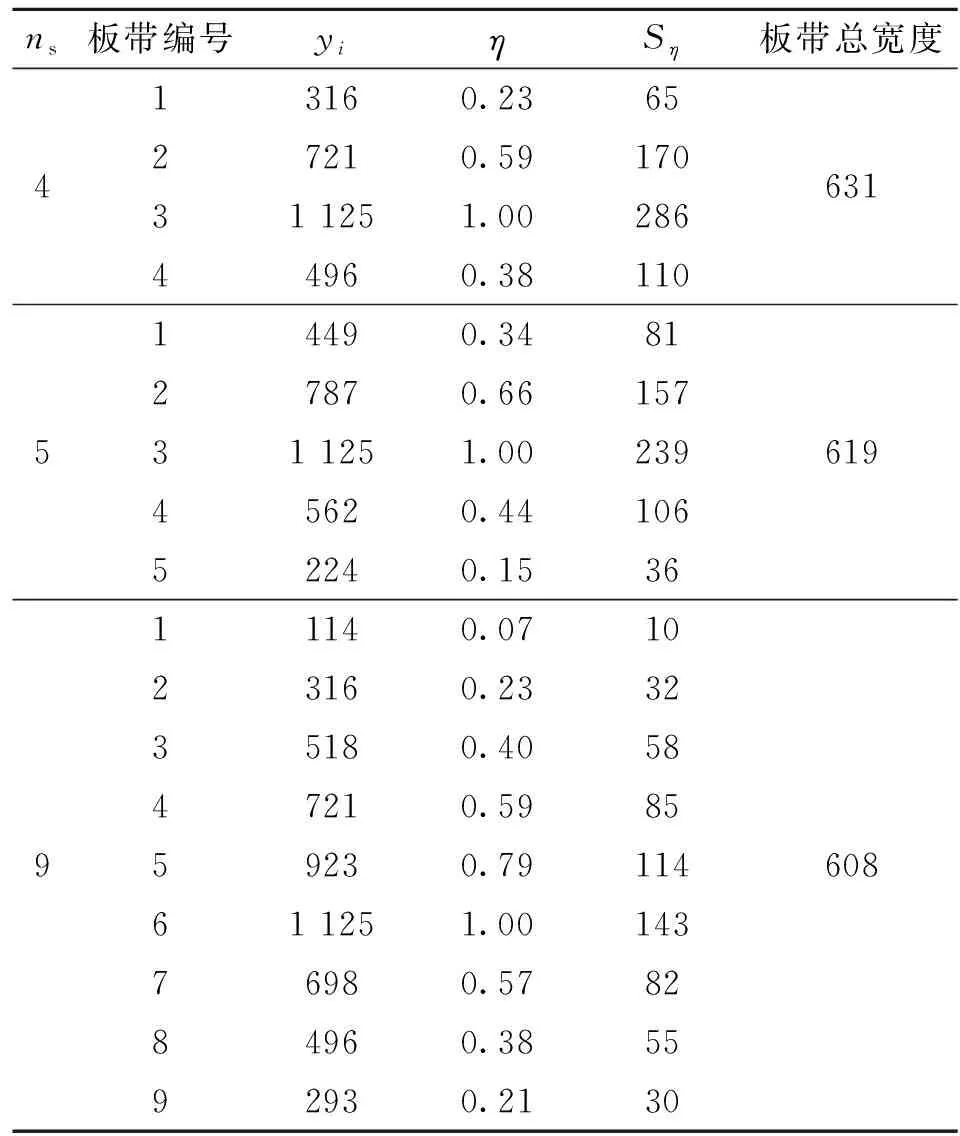
表2 斜向板带宽度取值Tab.2 Value of diagonal strip width
由式(1)计算不同板带数下斜向板带的宽度,计算结果汇总于表1。
斜向板带有效宽度调整系数η按下式计算[6]:
(2)

因此,各斜向板带的有效宽度Sηi=ηi×S。沿斜向板带模型的左下角至右上角对各板带依次进行编号,对各斜向板带的有效宽度进行计算,部分计算结果汇总于表2(ns=4、5、9)。由表2可知,当斜向板带模型的板带数不同时,其板带总有效宽度相差不多。
3 有限元分析过程
为验证有限元分析方法的正确性及等效斜向板带模型对于钢框架内填再生混凝土墙结构的适用性,分别对有限元整体模型及斜向板带模型进行了分析。有限元整体模型及斜向板带模型(ns=4)见图5,其中,X轴表示模型的水平向,Y轴表示模型的竖向。

图5 有限元模型Fig.5 Finite element model
3.1 材料模型与参数
钢材采用多线性等向强化模型,屈服强度、抗拉强度及弹性模量的取值见表3;再生混凝土选用混凝土损伤塑性模型[10],再生混凝土抗压强度实测值为32.8 MPa。

表3 钢材材料参数Tab.3 Material parameters of steel
再生混凝土单轴受压应力-应变关系:
(3)
(4)
式中:a为再生混凝土单轴受压应力-应变曲线上升段参数,b为下降段参数,fc为再生混凝土抗压强度,ε0为再生混凝土峰值压应变。
再生混凝土单轴受拉应力-应变曲线上升段参照文献[11]建议的公式,曲线下降段参照《混凝土结构设计规范》(GB50010—2010)[12]建议的公式:
(5)
(6)
式中:c为反映混凝土初始弹性模量的参数,d为混凝土单轴受拉应力-应变曲线下降段参数,ft为混凝土抗拉强度,εt为混凝土峰值拉应变。
3.2 单元选取
整体模型梁、柱、内填墙板等均选用C3D8R实体单元,钢筋骨架选用T3D2桁架单元;斜向板带模型梁、柱及斜向板带均选用B21梁单元。
3.3 约束与边界
在试验加载过程中,钢框架与内填墙板之间未发生相对滑移,两者之间连接牢固,因此整体模型钢框架与内填墙板的连接设置为绑定约束,梁柱连接也设置为绑定约束;为防止加载点处应力集中,在荷载施加平面建立耦合约束;钢筋混凝土采用嵌入式滑移模型,将钢筋骨架内置于混凝土中,并认为钢筋与混凝土粘结很好,忽略钢筋与混凝土的相对滑移;约束模型底部所有自由度,有限元模型见图5(a)。
斜向板带模型钢框架与斜向板带之间建立MPC铰接,钢框架底部设置为U1、U2、UR3=0(固结),斜向板带底部设置为U1、U2=0(铰接),见图5(b)。
3.4 荷载施加
第一步施加250 kN竖向荷载,第二步施加25.0 mm单调水平位移荷载,25.0 mm为试验加载结束时的梁端水平位移。
4 结果对比分析
4.1 整体模型
有限元整体模型与试验模型单调荷载-位移曲线的对比见图6。

图6 整体模型荷载-位移曲线Fig.6 Load-displacement curves of whole model
由图6可知:整体模型的初始刚度略高于试验模型,但随着加载位移的增大,两者之间的偏差在逐渐缩小;峰值荷载也略高于试验模型,峰值荷载之后承载力有下降,但降低幅度不大。
有限元结果与试验结果存在一定的差异,原因分析为:试验模型在加工过程中会产生初始缺陷,安装过程也存在初始缝隙等,而有限元模型各部件、各部件之间的约束及底部边界等均为理想状态,所采用的材料属性也不能完全反映材料的真实性能,尤其在往复荷载作用下,试验加载后期内填墙板混凝土严重开裂、大面积压碎脱落(图7(a)),有限元分析所采用的混凝土本构属性很难反映这种状态。从单调荷载作用下混凝土的受拉损伤云图(图7(b))可以看出,内填墙板沿对角线方向受拉损伤严重,验证了内填墙板对角斜向板带传递大部分水平剪力。
4.2 斜向板带模型
图8(a)~(b)分别为试验模型、整体模型及斜向板带模型ns=4~6、ns=7~9的单调荷载-位移曲线对比。
中国—东盟博览会永久落户南宁,不仅为南宁吸引了大量的外部投资,也为南宁的旅游业带来了充足的客源。因此,中国—东盟博览会在推动南宁经济的同时,也使南宁旅游业整体质量的提高。东博会和旅游业的良性互动,使得两者融合发展,促进南宁城市竞争力。在中国—东盟博览会的影响下,南宁的旅游业不断向好向快发展;而南宁旅游业的完善也在一定程度上保证了东博会举办的质量。两者的互动迎来社会和谐发展共赢的局面。
由图8可知:1) 不同板带数的斜向板带模型初始刚度基本相等,承载能力随板带数的增加而变化,但变化幅度不大。2) 斜向板带模型的初始刚度略高于试验模型,而与整体模型基本相等。当板带数ns=4~6时,斜向板带模型在加载后期承载能力无下降;当板带数ns=7~9时,斜向板带模型在加载后期承载力出现大幅度下降,且三者峰值位移基本相等,峰值荷载高于试验模型,荷载-位移曲线与试验曲线吻合较好。

图7 试件破坏形态Fig.7 Failure mode of specimen
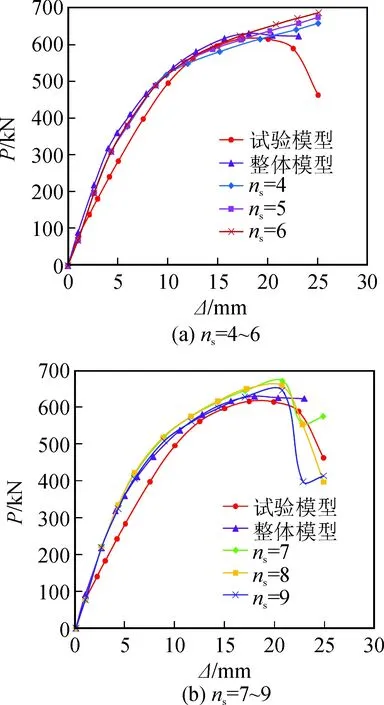
图8 斜向板带模型荷载-位移曲线Fig.8 Load-displacement curves of diagonal strip model
当板带数ns=7~9时,通过分析斜向板带模型的变形曲线(图9),发现斜向板带模型在加载后期承载力下降的原因为主受压板带产生了较大的屈曲变形。

图9 斜向板带模型变形图(ns=8)Fig.9 Deformation diagram of diagonal strip model(ns=8)
对主受压板带受力分析可知:在正向水平荷载作用下,主受压板带为两端受压的细长杆,虽然不同板带数斜向板带模型的斜向板带总有效宽度相差不多,但主受压板带的有效宽度随板带数的增加而减小,其受压失稳临界荷载Fcr也相应减小。随着水平荷载的持续增加,当主受压板带传递的压力达到其临界荷载时,会发生受压失稳,产生屈曲变形,导致主受压板带对结构承载力的贡献逐渐减弱,结构承载力出现大幅度下降。
4.3 偏差分析
当板带数ns=4~6时,斜向板带模型的单调荷载-位移曲线在加载后期承载力无下降,因此,只对有限元整体模型及板带数ns=7~9的斜向板带模型的峰值荷载、破坏荷载与试验模型进行偏差分析,计算结果汇总于表4。
由表4可知:
1) 有限元整体模型的破坏荷载与试验模型偏差较大,原因为整体模型在加载后期承载力下降较少,但两者的峰值荷载相差较小。可见,有限元分析能较好地模拟钢框架内填再生混凝土墙结构在单调荷载作用下的承载力变化。

表4 偏差分析Tab.4 Difference analysis
2) 板带数ns=7~9的斜向板带模型的峰值荷载均略高于试验模型及整体模型,原因分析为:斜向板带模型是一种桁架模型,以桁架的受力模式传递水平剪力,因此,当采用混凝土抗压强度作为力学性能指标时,将会高估试件的抗剪承载力。斜向板带模型的峰值荷载、破坏荷载与试验模型的偏差随板带数的增加而减小,且当板带数ns=9时,两偏差均在10%以内。因此,钢框架内填再生混凝土墙结构斜向板带模型板带数的合理取值为ns≥7。
5 参数扩展分析
通过改变钢框架内填再生混凝土墙结构的高跨比、内填墙板厚度及再生混凝土强度等参数,来分析不同设计参数对斜向板带模型板带数取值的影响。
5.1 高跨比
试验模型的内填墙板高度h=900 mm,内填墙板宽度l=1 125 mm,高跨比h/l=1.14,参数分析高跨比参数取值见表5。
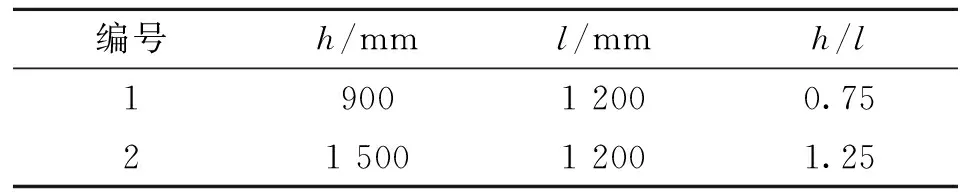
表5 高跨比参数Tab.5 High span ratio parameters
不同高跨比下整体模型与斜向板带模型的单调荷载-位移曲线对比见图10。

图10 不同高跨比下荷载-位移曲线Fig.10 Load-displacement curves of different high span ratios
由图10可知:1) 钢框架内填再生混凝土墙结构的初始刚度和承载力随高跨比的减小而提高,高跨比从1.25减小到0.75时,试件承载力提高约20%。2) 当高跨比=0.75,斜向板带模型板带数ns=9时,加载后期承载力有下降;当高跨比=1.25,斜向板带模型板带数ns≥6时,加载后期承载力均下降。可见,钢框架内填再生混凝土墙结构斜向板带模型板带数的合理取值随高跨比的减小而适当增加。
5.2 墙板厚度
试验模型的内填墙板厚度为90 mm,参数分析内填墙板厚度TIW取70 mm和110 mm。
不同内填墙板厚度下整体模型与斜向板带模型的单调荷载-位移曲线对比见图11。由图11可知:1) 钢框架内填再生混凝土墙结构的初始刚度和承载力随内填墙板厚度的增加而提高,墙板厚度每增加20 mm,试件承载力提高10%左右。2) 当墙板厚度=70 mm,斜向板带模型板带数ns≥6时,加载后期承载力均下降;当墙板厚度=110 mm,斜向板带模型板带数ns≥8时,加载后期承载力有下降。可见,钢框架内填再生混凝土墙结构斜向板带模型板带数的合理取值随内填墙板厚度的增加而适当增加。

图11 不同内填墙板厚度下荷载-位移曲线Fig.11 Load-displacement curves of different thicknesses of infilled wall
5.3 混凝土强度
试验模型的再生混凝土强度为C30,参数分析混凝土强度取C20和C40。
不同混凝土强度下整体模型与斜向板带模型的单调荷载-位移曲线对比见图12。由图12可知:1) 钢框架内填再生混凝土墙结构的承载力随混凝土强度的提高而提高,混凝土强度从C20提高到C40时,试件承载力提高约10%。2) 当混凝土强度=C20,斜向板带模型板带数ns≥6时,加载后期承载力均下降;当混凝土强度=C40,斜向板带模型板带数ns=9时,加载后期承载力有下降。可见,钢框架内填再生混凝土墙结构斜向板带模型板带数的合理取值随再生混凝土强度的提高而适当增加。

图12 不同混凝土强度下荷载-位移曲线Fig.12 Load-displacement curves of different concrete grades
6 结 论
1) 有限元分析的初始刚度略高于试验结果,随着加载位移的增大,两者之间的偏差逐渐缩小;峰值荷载也略高于试验结果,峰值荷载之后承载力下降较小。可见,有限元分析能较好地模拟钢框架内填再生混凝土墙结构在单调荷载作用下的整体性能。
2) 斜向板带模型能较好地反映单调荷载作用下钢框架内填再生混凝土墙结构的受力性能,其初始刚度略高于试验模型,与有限元整体模型基本相等。当板带数ns=7~9时,加载后期承载力出现大幅度下降,峰值荷载高于试验模型,荷载-位移曲线与试验曲线吻合较好。
3) 钢框架内填再生混凝土墙结构的高跨比、内填墙板厚度对结构的初始刚度和承载力有较大影响,高跨比从1.25减小到0.75、墙板厚度从70 mm增加到110 mm时,承载力提高约20%;再生混凝土强度从C20提高到C40时,承载力提高约10%。
4) 钢框架内填再生混凝土墙结构斜向板带模型板带数的合理取值为ns≥7,且随着结构高跨比的减小、内填墙板厚度的增加和再生混凝土强度的提高而适当增加。

