高等数学引领下的初等问题
——从一道八省联考试题的探究说起
朱世杰 (苏州大学数学科学学院 215006)
1 问题提出
导数是高等数学背景下的初等数学问题的典型,是引领学生开启微积分学习的金钥匙,是解决函数、方程和不等式等问题的有力工具,是联系初等数学与高等数学的桥梁和纽带,也是高考命题的热点、亮点和创新点.2021年全国八省联考数学试题以其科学性、前瞻性、灵活性和创新性而引人瞩目,其中具有代表性的第8题是:
已知a<5且ae5=5ea,b<4且be4=4eb,c<3且ce3=3ec,则( ).
A.c C.a 本题以方程与函数为背景,以不等关系的判断为目标,以导数为解题工具,以等价转化、函数与方程、数形结合和分类讨论思想为依托,入口宽、方法广、观点新、立意深,蕴含着丰富的数学知识和思想方法,具有很高的探究价值. 通过对问题的深入思考和研究,能够挖掘出问题的本质和内涵,发现问题间的内在联系,同时培养良好的思维习惯,提高提出问题、分析问题和解决问题的能力,打开通往数学科学殿堂的大门. 图1 图2 图3 图4 A.a C.c (1)求函数f(x)的单调区间; (2)设a>0,求函数f(x)在[2a,4a]上的最小值; (3)若存在正实数a,b(a 模型应用 已知定义在(0,+∞)上的函数f(x)满足xf′(x)-f(x)<0,其中f′(x)是函数f(x)的导函数,若f(m-2 021)>(m- 2 021)f(1),求实数m的取值范围. 极值是函数的重要性质之一.从以上六个函数模型的图象可以看出,它们与最基本的二次函数的极值相比不具有对称性,即极值点偏移了,而函数极值点偏移问题恰恰就是全国高考数学命题的热点之一. (1)求函数f(x)的单调区间和极值; (2)若函数y=g(x)对任意x满足g(x)=f(4-x),证明:当x>2时,f(x)>g(x); (3)若x1≠x2,且f(x1)=f(x2),证明:x1+x2>4. x(-∞,2)2(2,+∞)f'(x)+0-f(x)↗极大值↘ (3)由f(x)在(-∞,2)内是增函数,在(2, +∞)内是减函数.故当x1≠x2且f(x1)=f(x2)时,x1,x2不可能在同一单调区间内.不妨设x1<2 数学学习重在对概念、性质、定理、公式和法则等的理解和应用,重在对基础的夯实、思维的激活、方法的应用、能力的提升和解题后的反思.具体包括: 数学是用概念来思考问题的,所以对数学概念的理解尤为重要.由于数学内容的逻辑性强、抽象程度高,数学学习时必须先有浓厚的兴趣和刻苦钻研的精神,其次要能独立思考和实践探索,还要敢于质疑和挑战权威.只有扎扎实实、循序渐进地打好基础,静下心来去思考问题的内涵和外延,才能更好地学习数学. 建构主义学习观认为,知识并不是简单地由教师或其他人传授给学生,而只能由学生依据自身已有的知识、经验,主动加以建构.换句话说,数学学习必须以学习者的自主建构为基础,以数学探究为手段,以学会学习为核心,以实现探究精神和实践能力为目标. 爱因斯坦曾说:“提出一个问题往往比解决一个问题更重要.因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题,却需要有创造性的想象力,而且标志着科学的真正进步.”理解概念、学会推理、领悟思想、掌握方法是数学创新的基础,善于发现和提出问题才是创新的源泉.当你能够创新时,创新和发现就犹如数学家玻利亚所说,“在你找到第一个蘑菇时,继续观察,你就能发现一堆蘑菇.”这将是我们学习者追求的真正目标.2 问题解法探究




3 展开联想,借题发挥
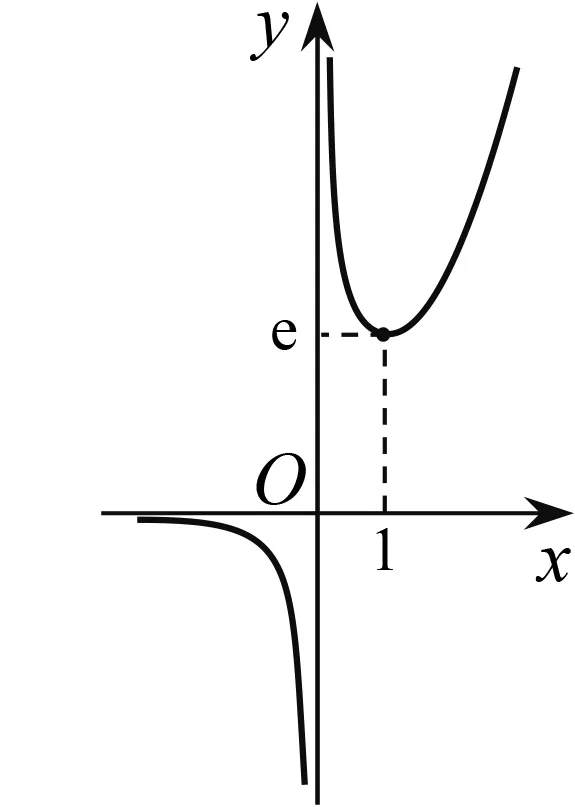
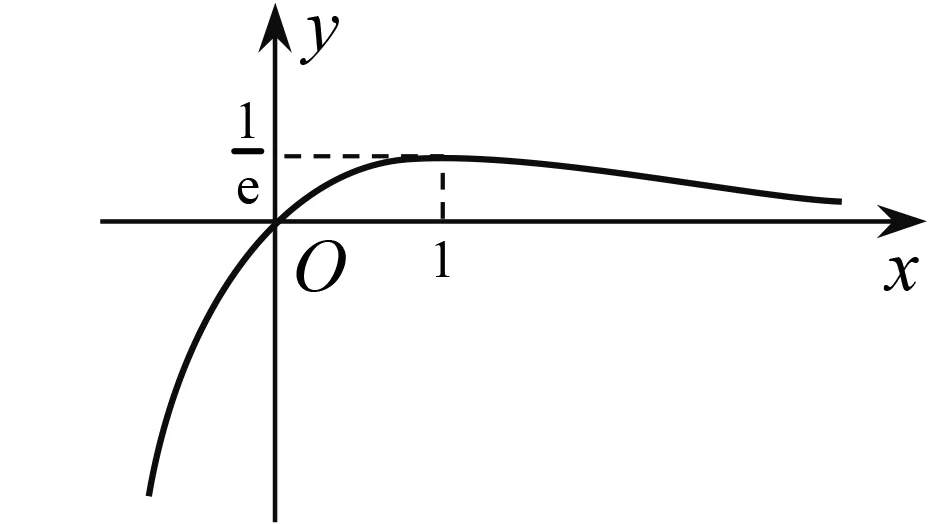
3.1 借题发挥:研究常见函数模型





3.2 借题发挥:构造原函数模型


3.3 借题发挥:解决极值点偏移问题


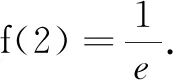

4 对数学学习的理解
4.1 数学学习重在基础
4.2 数学学习重在探究
4.3 数学学习贵在创新

