概念教学贵在挖理辨别——以“导数的概念”教学为例

孟凡敏 (江苏丰县中学 221700)

随着新一轮课改的推进以及对教学研究的深入，数学学科日显重视对知识本质的考查．透过现象回归概念本质成为教与学的必然，但课堂中重应用轻概念形成过程的教学现象比比皆是，因此研究如何提高概念教与学的有效性迫在眉睫．本文以人教版选修2-2导数概念的教学为例，按照实际的课堂教学顺序，结合具体的例题，从“教”和“学”两方面阐述如何进行挖掘、辨析，展示数学概念教学研究的过程．

1 教概念贵在“挖”理

把概念教给学生不在于记忆，也不在于让学生会简单模仿进而做题，而在于讲清概念中所蕴含的“道理”,包括探索概念形成的来龙去脉、品味概念表述中关键词的恰到好处、挖掘概念教学中蕴含的思想方法等.

集合、函数、数列……列举高中数学所学的概念，无论是涉及到的知识，还是从高考考查重要性的角度，导数都只能算是一个“小概念”．正是有了这个理由，大多数教师在讲授相关内容时往往舍本逐末，断章取义，甚至一笔带过，掩盖了许多宝贵的教学资源，以及教学过程前移的理念.只有静下心来做个有心之人，才能够挖掘出其中躲在这个“小概念”背后的“大道理”，而且这些也正是学习数学必需的观点、品质和思想．

1.1 挖掘概念引入，探析“事物普遍联系的 观点”

学生接受新知识的过程中，从已知到未知、从简单到复杂、从具体到抽象，这些矛盾对立的两个方面都需要运用联系的观点加以牵线搭桥．数学与其他学科、数学内部的各分支之间、同一教学内容的各个环节之间都有紧密的关系.只有揭示出知识间的联系，才能有助于学生对新知识的深刻理解，进而建立新旧知识的联系，培养学生学习数学的兴趣，真正提升学生的核心素养．

物理与数学是两门息息相关的学科，数学概念的理解和掌握常常需要借助物理意义的直观感知，而物理知识的逻辑严密性离不开数学的演绎推理．导数概念涉及抽象的极限思想，而物理中的位移、速度对高二学生来说却是比较熟悉的概念，借助平均速度与瞬时速度的类比分析，不仅赋予了导数概念中平均变化率与瞬时变化率以具体的物理意义，而且使得分析更加亲切、自然、充分，符合学生的认知规律．

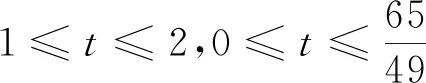
问题的设置层层递进，从平均速度(变化率)的计算，到引进瞬时速度(瞬时变化率，即导数)的必要性，再到瞬时变化率的计算，运用联系的观点，分析过程密切配合导数概念的生成．

1.2 挖掘概念表述，培养“咬文嚼字”的数学品质

众所周知，数学的定义以科学性、严谨性而著称，有多少数学人为高等数学中极限的ε-δ定义所折服．因此，学好数学、对数学定义的把握需要“咬文嚼字”的磨刀功，特别是对其中的关键字眼，需要多问几个为什么——不这样表述为什么就不行？不同定义的内涵和外延有什么区别？等等.这个过程中，举反例是最常用的手段．

例2判断函数y=|x|在x=0处是否可导.

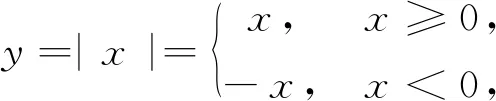
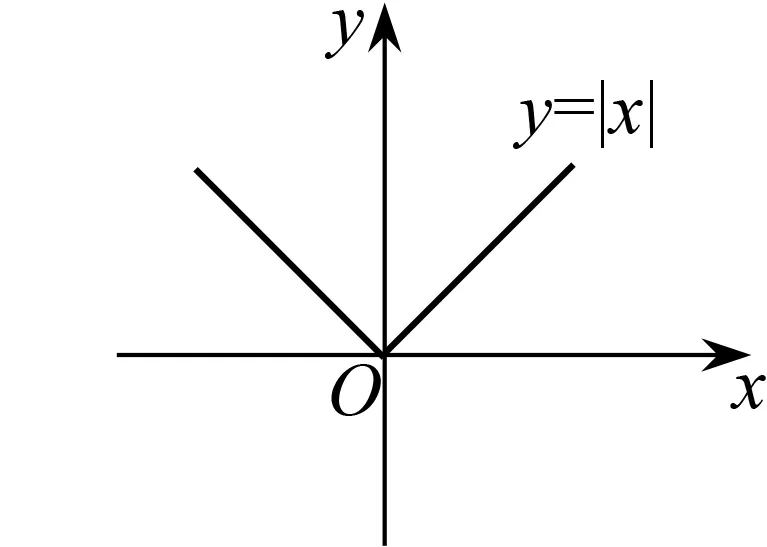
图1

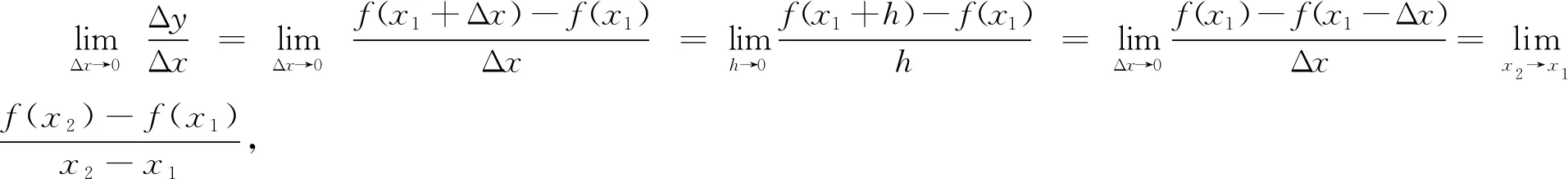
1.3 挖掘概念题解，培养数学解题中的目标意识

从某种意义上讲，数学解题就是在条件与结论之间“牵起”手来.这就不仅需要“由因导果”的综合思维，也需要“执果索因”的分析思维，缺少条件的结论最后是“无源之水”，而没有结论为目标的条件必然失去方向，解题具有目标意识就是这两种思维的有机统一．

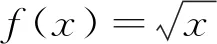
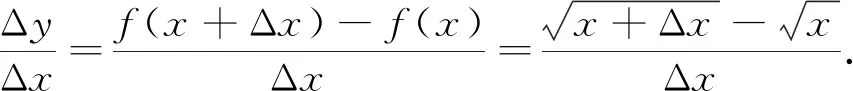
1.4 挖掘解题策略，提炼数学思想

提高学生分析问题和解决问题的能力是数学教学的根本目的.数学思想的渗透是数学教学的灵魂，而概念教学正是完成这一目标的主要路径．中学阶段最常见的数学思想有分类讨论、数形结合、方程思想等．

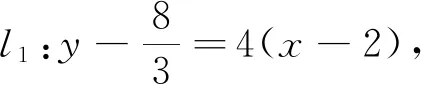
本题在求过点P的切线方程时，关键是求得切点坐标．因此需要运用方程思想，以设切点为入口、列方程组为核心、解未知数为目标．

图2

综上，教师教概念需要在系统、辩证、联系等高观点下授人以渔．

2 学概念重在辨别

学生在学习数学概念的历程中不仅要了解知识的形成过程，使得概念水到渠成并形成一个系统，更要善于对比，找出新旧概念的区别和联系．学生需要在争鸣和讨论中理解数学的本质，特别是概念的内涵和外延，挖掘知识的内涵，明确解题过程的科学性和严密性，从而有效培养各种数学思维和解题能力．

2.1 辨平均变化率与导数之别

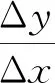
结合定义，导数即瞬时变化率．从平均变化率到导数，这不仅仅是概念上的简单转变，更是从静态到动态、从有限到无限、从量变到质变在思维方式上的突变，即极限思想．这一过程是一种趋向，非常抽象，似乎只能意会而不能言传，所以辨析时可以借助物理中的平均速度和即时速度、几何中的割线斜率和切线斜率．

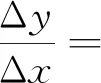
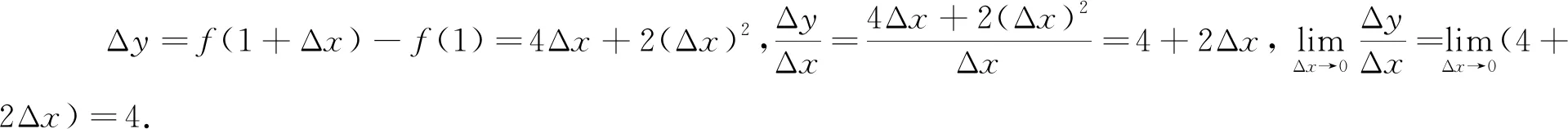
2.2 辨函数的图象和导函数图象之别

概念教学过程要正确理解函数图象和导函数图象的区别，切勿混淆．同时要理解它们的关系，也就是导函数的符号确定了函数的单调性，它的结果决定函数值的增长或减少的速度快慢，但是与函数值的大小没有关系，导数为零的点可能是极值点．

例6已知函数y=f(x)的导函数图象如图3所示，给出下列判断：

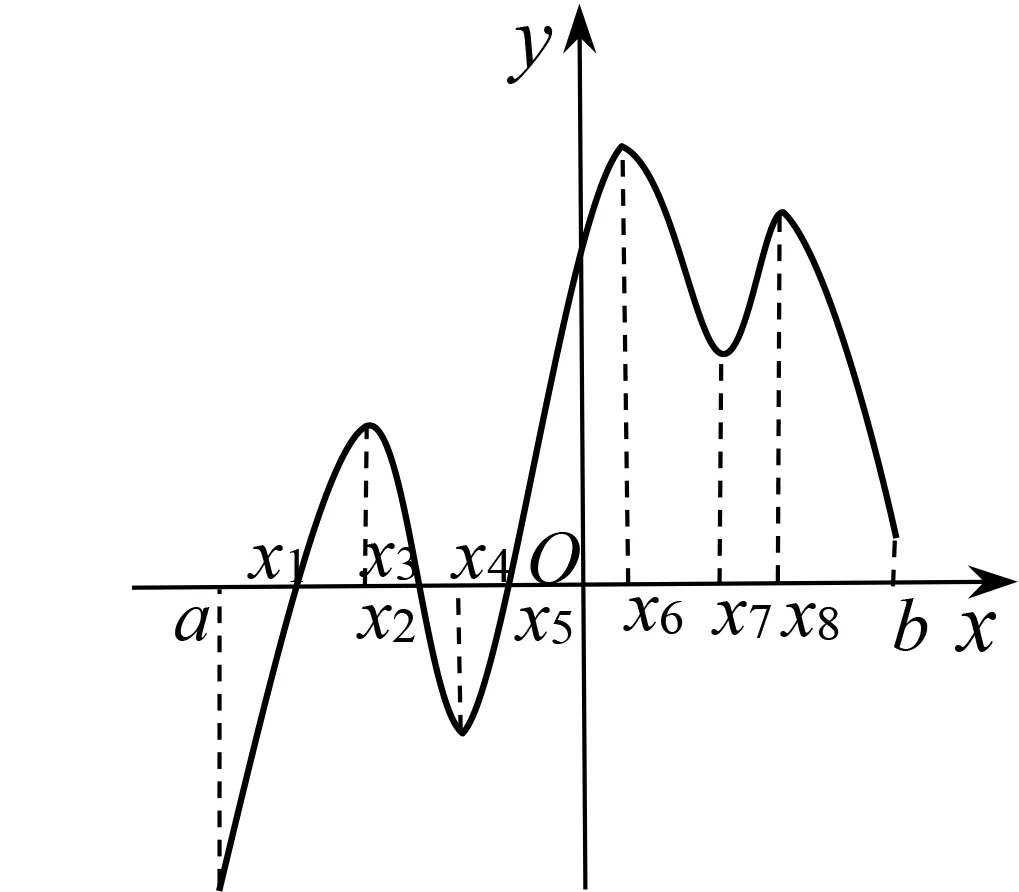
图3

(1)函数y=f(x)的单调递增区间有[x1,x3],[x5,b]；

(2)函数y=f(x)的单调递减区间有[x2,x4],[x6,x7],[x8,b]；

(3)函数y=f(x)在x4,x7处取到极小值；

(4)函数y=f(x)只有在x3处取到极大值；

(5)函数y=f(x)有ymin=f(a),ymax=f(x6)；

(6)函数y=f(x)在x6处存在较快的增长率，也就是对应函数在这个点处的切线斜率是最大的．

上述判断结果正确的是．

解析结合上述论述分析可得到，判断正确的是(1)，(4)，(6)；一定要注意与原函数图象区别开，避免得出(2)，(3)，(5)这样的错误结论．

2.3 辨导数大(小)于零与函数单调递增(减)之别

众所周知，在函数可导的条件下，若区间上有f′(x)>0(f′(x)<0)，则函数单调递增(减)；在区间上f′(x)=0，则f(x)=c(常数)．要结合函数y=x3的单调性和其在x=0处导数等于零得到如下结论：若函数的导数只能在“有限”个点处取到零值，则函数单调性保持不变，因此导数大(小)于零是函数单调递增(减)的充分非必要条件．

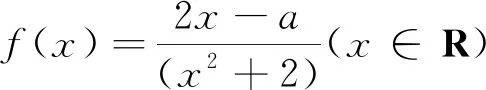
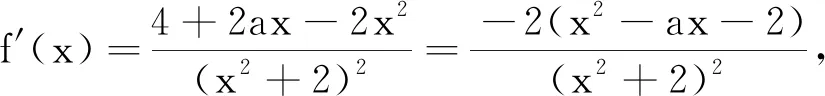
2.4 辨在区间[a,b]上具有单调性与单调区间为[a,b]之别

由例6可知，函数y=f(x)在区间[a,b]上单调递增(减)，是指[a,b]落在单调递增(减)的自变量范围内，这个函数的导函数在此区间上大(小)于等于零恒成立.而函数y=f(x)单调递增(减)区间为[a,b]，则说明[a,b]是唯一的单调递增(减)区间，特别地，对连续的初等函数而言，x=a,x=b是相关导函数方程f′(x)=0的两个根．

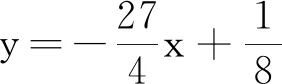
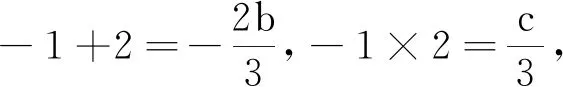
综上，学生学概念需要在质疑、解疑的不断思维碰撞中辨析并理解概念.

3 结束语

3.1 教师挖掘从微研究开始

无论是数学概念内涵的“挖掘”，还是其他数学教学内容的讲解，初教者往往存在形式上机械传授、内容上使用简单化、问题解决表面化以及教师讲授与学生脱节等问题.“纸上得来总觉浅，心中悟出方知深”，年轻教师要从“教教材”向“用教材教”转变，这个过程不能一蹴而就，需要静心思考、潜心研究，数学研究能力的提高是一个循序渐进的探索过程.

3.2 学生积极参与是课堂的最高境界

学生的数学学习活动应倡导动手实践、自助探索、合作交流等学习数学的过程，而不是仅局限于被动接受、机械记忆、单纯模仿的过程．这些方式有助于发挥学生学习的主动性，真正使学生的学习过程变为是在教师引领下的“再创造”的学习历程．本文中导数概念辨析的对象和问题绝大部分由学生提出，而其结论基本上也是由学生自行讨论并解决．在辨析过程中，学生获得的不仅仅是知识上对导数本质的把握，更重要的是培养了学生追求真理、锲而不舍的学习精神，以及辩证的数学思维方法和良好的数学素养．相信学生享受了这一学习的过程，其中成就感带来的愉悦是单纯的解题不能给予的，因为兴趣永远是学生最好的老师．

3.3 搭建师生“挖”与“辨”的研究平台

新课程教学理念指出：构建共同基础，筑建发展平台．现阶段由于教育行政部门对教师的短期考核(一般以学期为单位)，迫使一线教师急功近利，牢牢抓住根本没有战略但见效快的“题海战术”，数学教学缺少教师研究、特别是学生参与研究的平台．江苏省作为新课改、考改的试点省份，新方案提供了大量的选修课程，这为搭建这一平台提供了可能.我们数学工作者要以此为契机，努力倡导并不断实践，开发、开设数学“教”与“学”的研究课程．