例谈斐波那契数列的性质与应用*

陈潇春 惠 宇 (江苏省无锡市第一女子中学 214002)

1 引言

在新的高考改革中，与数学文化相结合的题目可谓百花齐放、百家争鸣，从鳖臑到日冕，从几何原本到九章算术，从维纳斯身高到故宫台阶级数，不仅检验学生的知识储备水平，更考查学生对所学知识的调用、迁移、转换、应用以及创新的能力，由点到面地考查学生的数学核心素养．本文试图通过对学生熟悉的数列研究方法的探究，例析斐波那契数列的相关性质与应用，并谈谈对此类与数学文化相结合问题的教学思考，以期抛砖引玉．如有不当之处，敬请批评指正．

2 斐波那契数列的性质及应用

斐波那契数列(Fibonacci sequence)是由 13世纪意大利数学家斐波那契在研究兔子繁殖问题时提出的，其独特魅力不仅在于它源于生活的现实应用之美，更在于它独有的数学理性之美．在探究性质、找寻规律的过程中所散发的理性与智慧，正是它流传至今并活跃于各地高考模考的重要原因．

设数列{an}为斐波那契数列，根据定义，数列{an}满足递推关系an=an-2+an-1(n≥3)，其前n项和记作Sn．

性质1Sn=an+2-1．

证明方法1(迭代法)an+2-1=an+an+1-1=an-2+an-1+an-1+an-1=an-2+(an-3+an-2)+an-1+an-1=…=a1+a2+a2+a3+a4+…+an=Sn.

方法2(定义法) 因为Sn-Sn-1=an=an+2-an+1，所以Sn-an+2=Sn-1-an+1(n≥2)，即{Sn-an+2}为常数列．从而Sn-an+2=S2-a4= -1，即Sn=an+2-1．

方法3(错位相加法)Sn=a1+a2+a3+a4+…+an-1+an，错位相加得2Sn=a1+(a2+a1)+(a3+a2)+…+(an+an-1)+an=a1+a3+a4+…+an+an+1+an，因此2Sn=(a1+a3+a4+…+an)+(an+1+an)=Sn-1+an+2，即Sn=an+2-1．

例1(2017—2018全国高三模拟训练改编)“斐波那契数列”是由十三世纪意大利数学家斐波那契发现的，数列中的一系列数字被人们称为神奇数．该数列的第三项数字开始，每个数字等于前两个相邻数字之和．已知数列{an}为“斐波那契数列”，Sn为数列{an}的前n项的和，若a2 017=m，则S2 015的值为( )．

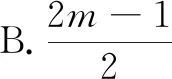
评析等差数列和等比数列是学生系统学习与探究的两类基本数列．在数列问题的研究中，迭代法、累加法、倒序相加或错位相减是常用的处理方法．此题以斐波那契数列为探究起点，需要学生灵活运用已有的解决数列问题的方法与技巧，在数学思想方法引领下创造性地探究该数列前n项和与an之间所满足的关系．不仅考查学生对知识的理解，也考查学生对数学思想方法的贯通、对数学思维方式的内化，体现从知识到能力、从技能到素养的评价方式的转变．

性质2a1+a3+…+a2n-1=a2n，a2+a3+…+a2n=a2n+1-1．

证明方法1(迭代法) 同性质1，略．

方法2(累加法) 以奇数项求和为例，a2n-1=a2n-3+a2n-2,a2n-3=a2n-5+a2n-4，…，a3=a2+a1，累加得a3+a5+…+a2n-1=a1+a2+…+a2n-2=S2n-2．由性质1，S2n-2=a2n-1，故a1+a3+…+a2n-1=a2n．

例2(2019湖北省随州高一调研改编)“斐波那契数列”又称黄金分割数列，因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”．在数学上，斐波那契数列以如下递推的方法定义：a1=1,a2=1,an=an-1+an-2(n≥3)，则a2+a4+a6+…+a2 018-a2 019=．

评析探究数列奇数项或偶数项的和是研究数列的基本问题之一．斐波那契数列并非教材中的基本数列类型．因此，对该数列前n项和的研究必然需要学生在掌握等差、等比数列求和公式的基础上，熟练掌握数列求和的基本方法，深入理解具体数列的本质特征，灵活应用数列求和的基本思想，实现知识的融合与思维的贯通.这样的问题综合考查学生知识的应用性、思维的创造性及素养的内化性．

证明方法1(迭代法) 同性质1，略.

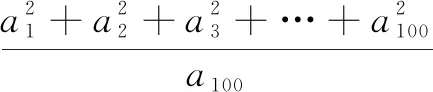
评析本题的处理关键是对代数式中分子上的数列各项的平方进行求和探究．此处，我们推导了斐波那契数列具有的性质3，不难将分子上的求和结果转化为a100a101，即可得到所求为斐波那契数列中的第101项．迭代法和累加法是研究此类数列问题的基本方法，斐波那契数列的递推关系不仅揭示了该数列的本质属性，即an=an-1+an-2(n≥3)，而且也为数列求和、数列性质的探究提供本源性的依据，并在探究过程中体现数学的创造性、思辨性、统一性，体现从知识评价到素养评价的评价方式的转变．

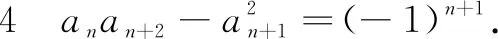
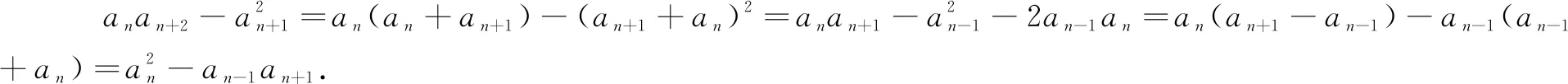
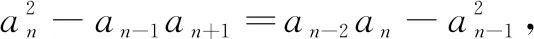
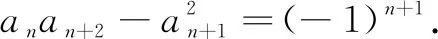
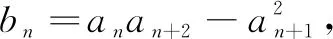
3 探究斐波那契数列性质与应用的教学思考

近年来，与数学文化相结合的考题屡次出现在全国各省模考和高考中，是评价学生数学学科素养的重要依据．据笔者不完全统计，斐波那契数列2019年出现在各省市高考模考中的次数有10余次之多，考查范围从对数列递推关系的理解到数列性质的综合探究，可谓灵活多样．在教学实践中，教师不可能将数学文化以知识的形式全然授予学生，数学文化更不应成为学生“甜蜜的负担”而丧失其宝贵的价值．笔者认为应从以下两点挖掘数学文化的育人价值，实现文化育人、立德树人的教学目标．

(1)以数学文化为依托，确立素养发展的生长点

数学文化是人类智慧的结晶，是数学学科得以发展、数学思想得以流传的重要依托．其蕴含知识的多样性、数学思想的丰富性、探究方法的开放性，正是培养学生创造性地使用所学知识，学会以数学的思维模式思考和解决问题的重要载体．因此，数学文化不仅是教学评价体系的重要组成部分，也是学科教学中不可或缺的一部分．在教学中，数学文化的合理有效的使用是学生素养形成和培养的重要起点．

新教材与原有的教材体系相比，进一步加强了数学文化在正文中的渗透．例如教材利用探究第24届国际数学家大会的会标，即赵爽的弦图，来研究相等关系和不等关系，实现基本不等式的一种图形表达．此外，新的课程体系更加注重学生课后的拓展性阅读和开放性探究，以“拓广探索”“阅读与思考”“探究与发现”“文献阅读与数学写作”为载体，将数学文化的浸润延伸到课堂之外．以数学文化为依托，学生创造性地使用所学知识解决新问题，思考新的探究方向，逐步形成理性思维、发散性思维和创新精神、思辨意识，实现由知识的习得到思维品质的提升，再到素养能力内化的自然提升．

(2)以数学文化为纽带，找准思维培养的关键点

数学思想方法的形成是数学核心素养内化的重要组成部分．数学文化中蕴含丰富的数学思想，然而数学文化如浩渺烟海，教学中我们应抓住其本质特征，在体现数学思想的本源性问题上引导学生深入探究，从思维立意的高度上高屋建瓴地对知识的本质进行理解和掌握．例如根据等比数列递推关系所揭示的数列特征，我们采用错位相减的方法对其进行求和．而斐波那契数列从第三个数起，每一个数都等于它前两个数的和，即an=an-1+an-2(n≥3)，类比错位相减的求和方法，学生很自然地想到通过错位相加进行求和．

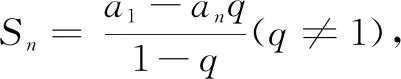
4 结语

斐波那契数列并非学生熟悉的基本数列，但探究中所需要的能力水平与思维模式正是学生对所学知识的迁移、对所学思想的理解、对数学学科素养内化程度的外在表现．在教学中，我们应鼓励学生从最基本的特征出发，以数学探究为起点，以数学文化为纽带，运用研究数学问题的基本方法去发现新的结论，拓展新思维，提升对新知的挖掘能力．这一过程也能让学生体会先贤对数学发展作出的卓越贡献、感受数学的理性之美，并赋予他们叩开数学之门所需的思维品质和精神动力．