溯源命题背景 厚重理性思维
金曦东 (江苏省苏州市吴中区东山中学 215107)
在问题解决中,溯源问题的背景,探索问题的由来,分析问题的结构,揭示问题最本质的内核,能够厚重解题的理性思维,让学生的思维更加沉稳.特别在高三复习中,很多高考原题受到教师的青睐,但很多时候教师关注的只是这个问题怎么解,如何优化解法.而命题的背景是什么?命题的本意是什么?这些问题往往被淡化了.笔者认为,通过正本溯源与命题专家心灵对话,求变求新形成自己的感悟,让思维八方联系浑然一体,是提升复习效率的重要途径.
1 心灵对话,会意命题意图
数学问题的解决历来是数学教学的核心.命题者要考什么和考生怎么解题,是两个不同的思维轨道.当这两个思维轨道交汇的时候,才能充分达成命题者的意图,学生也可能得到最大的解题效益,这在高三复习阶段尤为突出.数学问题的解决,有各种不同的途径和方法,还要经历直观感知、观察发现、归纳类比、空间想象、抽象概括、反思构造等一系列思维过程,以及对数学模式进行思考并作出判断,这就注定了“一千个观众眼中有一千个哈姆雷特”.而有的方法只能说是就题论题,人为技巧化的痕迹很明显,看问题的角度也过于生冷,有的甚至过分强调问题的细枝末节,这对学生形成理性思维是没有多大帮助的.通过分析、比较,从基础知识、基本技能、问题模型和思想方法层面,探寻更接近命题意图的东西,与命题专家进行隔空心灵对话,理解专家希望考查什么知识、希望学生掌握什么思想方法,又将什么能力外显,触摸问题的背景,会意命题的意图,揭示问题本质,这是对问题有针对性、深层次的观察.
2 正本溯源,厚重理性思维
发展学生的数学思维,提高学生发现问题、分析和解决问题的能力,是高中数学课程的基本目标.高三复习,应比平时的新课教学在思想上、方法上、教学行为等方面站得更高、看得更远,并尝试性地做一些突破性的工作.“夯实基础,突出主干、揭示本源、提升能力”为高三复习的核心任务.数学教学不是以解释问题为目的、而是以解决问题为根本,问题解决在很大层面上是对问题结构的认识,正本溯源才能更好地接近问题的本质,才能为最终解决问题创造条件.正本溯源是高三复习的精神要求,是促进学生形成理性思维,提高复习效率的有效途径之一.当然,正本溯源是不可能一蹴而就的,必须建立在学生基础已经夯实,知识体系网络化初步形成,基本方法、基本技能、基本思想初步具备的前提下.同时,这对教师应当具备的专业素质也提出了更高的要求,教师不仅要有“揭示本源”的准备,还要有提高认识的决心、行动策略和付诸实践的勇气和耐心.
3 问题解决,明晰思维指向
正本溯源,重在明确思维的指向.如,数学的核心概念、结构分析、信息优化、数学的思想方法以及数学结论、法则的本质等,都是正本溯源的重要关注点.高三复习课教学设计、学生检测卷的编制以及评析等诸多环节,都需要注重从数学问题立意的角度去分析.多角度、多层次分析解题的思维过程,并从知识层面、方法层面、能力层面加以比较,使解决问题的方法更贴近命题者的期盼,对接命题的出发点、落脚点.
3.1 回眸概念,区分考察层次
数学概念尤其是数学的重点概念,历来是数学教学的核心,理应成为数学命题立意的基础.高考中,很少有单独命题去考查某个孤立的概念,比如正弦型函数问题,往往要围绕这个概念并辐射到有关图象、性质等关联内容,需要综合地、系统地分析问题.高三更应体现“核心概念”和“概念的核心”在复习中的地位,强调概念对数学本质认识方面的突出作用,在回眸概念中再认识问题.

分析 这道题是通过三角函数的概念、图象和性质,考查学生对三角函数性质的掌握情况,命题者的立意很明显是建立在对f(x)=sin(2x+φ)图象及其性质掌握的基础之上,解题方法也应当是直接瞄准这些基本内容.

教学中发现,不少学生采用了以下方法:
方法2 由题意知



尽管也运用了不等式思想以及三角函数的有关运算,但是方法2、方法3对f(x)=sin(2x+φ)根据条件所得到的函数图象和性质不清晰,在取值运算的过程中,完全无视三角函数性质和题目条件所暴露的图形信息,有理由认为方法2、方法3不是命题的最优意图,也似乎缺少一些更触及问题本质的理性思维.
3.2 分析结构,划归数学模型
在数学模型中建构数学问题是命题者重视的,发现问题背景模型,往往会带来“似曾相识”之感,更容易聚焦思维,给解题指明方向.特别是高考的应用问题,透过题目给出的一些生活、文化等信息,发现其背后的数学本质,建立起解题的数学模型,有效地将“生活化”的问题进行“数学化”,这是解这类题的必然思维轨道.
例2在数1和100之间插入n个实数,使得这n+2个数构成递增的等比数列,将这n+2个数的乘积记作Tn,再令an=lgTn(n≥1).
(1)求数列{an}的通项公式;(2)求bn= tanantanan+1的前n项和Sn.


前者运用了倒序相乘法这一模式化的方法,后者运用了等差、等比数列的定义及通项公式,仅从方法层面而言,尽管我们无法评判两种解法孰优孰劣,但是数学问题能够模式化解决,运用自己熟悉的范式,这是很多学生愿意而且希望看到的.

很多学生不能解决本例的根本原因,是对“裂项求和”模式不熟练,tanαtanβ常常在tan(α+β),tan(α-β)中见到,因此构造两角和、两角差的正切函数可以说是不二的选择,而在两角和与两角差之间也只能选择两角差的正切,这是裂项求和模式的需要.数学问题模式化尽管不能过于强调,但是也不可或缺,增加数学模型的储备是非常必要的.
3.3 优化信息,显现核心本质
捕捉、提取和加工解题信息是解题活动中最为关键、最为基础的环节,势必会成为数学问题立意的热点.从信息的来源看,一方面是从“双基”中获取的信息,如相关的数学定义、概念、法则、结论,数学思想方法,题型特征等.另一方面是从题设、题断中提取的信息,如位置信息、数值信息、结构信息等.这些是高三复习中的重要关注方向之一,决定了能不能看透问题的本质以准确剖析问题.


这种解题方法考查了不等式的性质、代数恒等变形的能力和推理论证能力,而且运用的是不等式证明中的通性、通法:作差法.私自揣摩,这或许并不违背命题意图.但是,总感觉有些不自在和不踏实,因为这道题结构特征那么明显.



从方法2可以看出,这种解法与数学问题的结构信息相关联,它不仅贯穿了函数的单调性并且有很“浓厚”的函数思想,思维增加了一些灵动.
3.4 应对沉稳,积淀思想方法
以数学思想、方法和能力立意的数学问题,不仅要注重逻辑推理,更要领会形式化表达背后所蕴涵的思想方法,这是数学问题立意中最隐性也是最难以把握的.形式化表达是数学的基本特征之一,在数学教学中,要透过形式化的表达,强调对数学本质的认识,揭示其蕴涵的思想方法,使思维在积淀中沉稳.

(Ⅰ)当x∈(0,x1)时,证明:x 分析 这道题在形式化表达的背后有几个关键问题: (2)已知条件中有x2,而在求证中没有x2,那么x2的作用是什么?如何发挥x2的作用? (3)研究对象是y=f(x)还是F(x)=f(x)-x? 观察图象,在形式化表达上揣摩立意背后的数学思想,如不等式思想、方程思想、函数思想、数形结合的思想,更进一步探究其背后的内在联系,以及逻辑结构和核心,提出几方面的探索: 图1 考虑到二次函数的对称性以及0 从方程、不等式的角度,可以构造F(x)=f(x)-x=a(x-x1)(x-x2),这是目前最常见的解法,这里不再赘述. (2)x2的作用是什么? 从数形结合的角度看x2的作用,它是在确定y=f(x)对称轴的位置上发挥了作用.但是,从不等式、方程的角度看是起放缩比较的作用. ①求证:x 设F(x)=f(x)-x,因为F(x)=0的根是x1,x2,所以F(x)=a(x-x1)(x-x2).当x∈(0,x1)时,由于x1 ②求证:f(x) 这个过程也蕴含了问题(3)的回答.从以上分析看,对数学问题立意的分析、探究和归纳、概括,不仅走近了数学问题,了解了数学命题的意图、触及数学本质.更为重要的是在这一过程中,所运用的数学概念、法则、结论更明确、合理,更容易判断.同时,在这一过程中充分暴露了解题思维的全过程,以及蕴涵其中的数学思想方法,这对提高学生思维品质,形成理性思维具有积极的意义. 磨砺始得玉成,会解题只是学习的初级阶段,通过对问题的正本溯源,对话命题本意,让学生把题目做得明白,知道为什么这么做.再通过进一步分解、组合、重构等一系列过程,探索问题和已知知识、熟悉问题的联系,建立已知和未知的通道,认清问题的本质,并对问题进行更深层次的变化,让思维更加理性,这应该是我们期盼的“解题教学”吧.



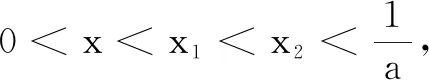


4 结语

