正确对待“低级”错误 用心授好“预备知识”

刘在云 (江苏省仪征市教学研究室 211400)

1 引言

2020级高一学生是我省使用新教材的首届学生.而全新的苏教版数学教材，是根据《普通高中数学课程标准(2017版)》(下称《新课标》)的指导意见，在必修第一册的前四章编排的是主题1——预备知识．根据编写的内容可以看出，教材已力求以义务教育阶段数学课程内容为载体，相同学习内容在老版教材基础上作了较大改变(可参看文[1])．结合集合、常用逻辑用语、相等关系与不等关系、从函数观点看一元二次方程和一元二次不等式等内容的学习，为高中数学课程做好学习心理、学习方式和知识技能等方面的准备，帮助学生完成初高中数学学习的过渡．

《新课标》为什么要求编排预备知识？笔者认为正是考虑到作为高中学习的内容，一开始就比初中时更加抽象、更加综合、更具有逻辑性，期望通过预备知识的学习，让学生有个适应过程．作为执教高一的数学教师，我们应加强对《新课标》的学习，领会《新课标》的精神，力求遵从学生认知规律，合理安排教学内容，揭示数学内容的发生、发展过程，体现数学内容的逻辑体系，同时也应在教学方式上勇于突破、积极创新，多多指导学生自主学习，切实让学生掌握高中数学必备知识，提高其关键能力，最终发展学生的数学核心素养，使其更好地适应三年后的基于高考评价体系的数学科的高考．如果我们不能更新教学理念，继续以满堂灌的形式讲解新知，并辅以大容量的练习，不但很难培养学生的核心素养和创新精神，可能连一些必备知识的掌握都困难重重，这首先就表现为一些“低级”错误屡屡发生，久而久之，会让部分学生畏惧数学，最终失去学习数学的兴趣和能力．

2 案例分析

案例1听课中发现的三个错误．

教学内容是用基本不等式求函数最值，源于苏教版普通高中教科书数学必修第一册第三章第一节《基本不等式》(2020年7月的第一版新教材)，教学对象是我市生源最好的老牌四星高中的一个普通班．

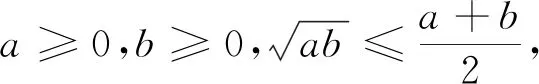
(3)在教师特别强调之下，仍未写上等号取得的条件．

错误(3)常被有些教师认为是学生态度问题，笔者认为不是如此，责任还是在教师，因为教师未能跟学生讲清为什么一定要写等号取得的条件，这就要从“函数的最值”定义谈起，当然此定义被苏教版教材编写于第五章(在本内容之后)，这就需要教师灵活使用教材．比如通过举例x2≥-1恒成立，但不能说x2的最小值是-1，先让学生感受到函数的最值一定要能取到，也就能够让学生认同用基本不等式求最值时一定要加上等号取得的条件，那是学数学必须有的严谨．

案例2单元检测中出现的错误．

题目：已知集合A={x|x2-2x-3=0},B={x|mx-1=0}，且B⊆A，求m的值．

说实话，作为初学集合的高一学生，首次面对此题，忽略集合B为空集而导致求解不全可以理解，但有位教师向笔者诉苦，说讲了不止一次，仍有部分学生不考虑集合B为空集的情况，开始质疑学生的学习能力．于是笔者就向这位教师询问是如何讲解的，教师说根据题意，先讨论集合B为空集，得出m=0，再讨论m≠0时的情况，然后叹惜学生就是不长记性，老是忘了B为空集的情况．笔者就反问这位教师：有人提醒你在一段你不经常走的路段上有个小坑，你偶尔经过时会想起那边有坑吗？该教师说：可能不会想到．因此笔者就说，那我们就要理解学生了，他们每天忙于多门科目的学习，每天都要学习许多新的内容，怎么可能一定记得这道题中的小坑呢？该教师马上表示赞同，笔者问到：那怎样可以避免受到坑的影响呢？我们只有养成认真走路，看路走路的素养．

这道题的讲评正好可以培养学生这一素质.通过对本题的讲评，我们应让学生领会：数学解题必经之路是化简.记得曾有专家说过：数学解题的过程就是连续化简的过程，而化简时必须考虑等价变形．如此题首先要对集合A,B进行化简，其中容易化得集合A={-1,3}，而集合B是关于x的含参方程的解集，如何解？等价转化为mx=1，然后两边同除以m，而在此处需要特别强调m是否为零，当m=0时，关于x的方程无解，即集合B为空集，符合题意．通过交流，这位教师赞同了这一处理方法，也觉得一开始就讨论B为空集有点突兀，没能抓准逻辑起点．

案例3教师交流时诉说的错误．

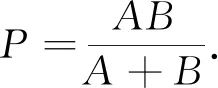
3 预备知识数学教学建议

(1)换位思考，降低难度

《新课标》开篇就介绍了课程性质与基本理念，而在基本理念中首先提到：高中数学课程以学生发展为本，落实立德树人的根本任务，培育科学精神与创新意识，提升数学学科核心素养．接着强调高中数学课程要面向全体学生，实现“人人都能获得良好的数学教育，不同的人在数学上得到不同发展”．为了践行这一理念，班级课堂教学目标的设定要研究学情(据了解,各地区不同学校高一生源情况有差异，同一学校不同班级之间也有差别)，备课时要全面关注学生的认知基础和现有能力，教学设计时要遵循学生的最近发展区原则．建议教师要能从学生角度体会一些数学知识，不能从自己的角度来看待一些教学内容，总是觉得这个内容这么简单，那个内容应该懂得，要多研究(当然也可向部分学生了解甚至可以全面调查)学生了解的程度.比如一元二次方程中的韦达定理，学生知晓情况的差别就很大．另外，为了最大程度地实现人人都能获得良好的数学教育，高一的教学安排(包括必要的测试)一定要降低难度，确保人人在数学的学习中有获得感与成就感，在学生犯一些“低级”错误时，教师要有包容心，要根据学生所犯错误分析其合理性，在保护其理性精神的基础上为其纠偏、纠错．

(2)找准起点，关注节点(理解数学)

(3)重视过程，增加探究

《新课标》在基本理念中提到，高中数学以发展学生数学学科素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质，提倡独立思考、自主学习、合作交流等多种学习方式，激发学生学习数学的兴趣，养成良好的学习习惯，促进学生实践能力与创新意识的发展．章建跃曾经谈到数学教学重结果轻过程的危害，他指出数学是思维的科学，数学思想方法孕育于知识的发生发展过程中，“思想”是概念的灵魂，是“数学素养”的源泉，是从技能到能力的桥梁；“过程”是“思想”的载体，是领悟概念本质的平台，是思维训练的通道，是培养数学能力的土壤．但事实上仍有一些教师的观念未能得到更新，数学课堂教学仍表现为轻过程、重结果、忙刷题.比如曾听过一节对数运算公式的新授课，教师在直接抛出公式，让学生短暂记忆后，就让学生利用公式进行解题，且坚持认为如此安排效率较高，认为这种公式教学目标就是知晓能用，而没能体会到如此安排严重丧失了本学科所应具备的培养学生思维能力、实践能力和创新意识的功能.事实上，对于这样的课堂，学生是不喜欢的，对于这样的教师，学生也是不欣赏的．