基于Hirota双线性方法的变系数BLMP方程的精确解
曹建莉,韩景芳
(河南工业大学理学院,河南郑州 450001)
1 引言
非线性发展方程可以描述各种现象随着时间变化的过程,涉及等离子物理、流体力学、生命科学、高分子材料系统等领域,因而,求解非线性发展方程显得尤为重要.本文考虑BLMP方程
uy t+uxxxy-3uxxuy-3uxuxy=0.
(1-1)
文献[1]将KdV方程推广到(2+1)维;文献[2]通过李群方法得到新的相似约化解,包括有理解、双曲函数解、Jacobi椭圆函数解和三角周期解;文献[3]获得了方程的变量分离解;文献[4]基于Bell多项式和双线性变换获得了方程的双线性Bäcklund变换和Lax对.文献[5]运用Hirota双线性方法,研究了方程的有理解、lump解及其解之间的相互作用.文献[6]得到了方程的碰撞解.
Hirota双线性方法、Wronskian技巧是求解孤子方程的重要方法.本文主要基于方程的双线性形式,利用Wronskian技巧和Pfaff式得到其Wronskian解和Grammian解,所得结果用Maya图进行表示.
2 BLMP方程的精确解
2.1 BLMP方程的Wronskian解
文献[7]中得到了BLMP方程的双线性形式、N-孤子解,并给出了一种Wronskian解.
令
u=-2(lnf)x,
(2-1)
将(2-1)代入(1-1),可得到BLMP方程的双线性形式
(2-2)
即
(fty+fxxxy)f-3fxxyfx-fxxxfy-ftfy+3fxxfxy=0.
(2-3)
Wronskian的定义如下:
(2-4)
设函数φj=φj(x,y,t)在t≥0,-∞ (2-5) 当Wronskian(2-4)在满足(2-5)的条件下,就得到(2-2)的Wronskian解. 在已有上述Wronskian解的基础上,设 (2-6) a,b,c,d只表示正负号. Grammian的形式如下: (2-7) 引入Pfaff式元素,根据Pfaff式的元素求导,将(2-6)的条件代入其中,则 在上述计算中,可得a,c同号,b,d同号,统一分别用e和f表示. Pfaff式的导数可由Pfaff式元素求导,并利用Pfaff式展开公式扩展到整体得到. 其中,Pfaff式中的{1,2,…,N,N*,…,2*,1*}用“·”表示. 将上述导数代入(2-3)式,得 再由-4-4f=0,得b=d=-1.则 所得结果对应的Maya图表为 结果为行列式的Jacobi恒等式.故(2-7)式在(2-6)的条件下,且b=d=-1时,为(2-2)的Grammian解. 2uy t+uxxxy+3uxxuy+3uxuxy=0. (3-1) (3-2) 则方程变为 puy t+uxxxy+quxxuy+quxuxy=0. (3-3) 作变换 u=R(lnτ)x, (3-4) (3-5) 文献[9]中王明亮和李志斌等教授提出了齐次平衡法构造孤子解,文献[10]中,利用相似的平衡法构造方程的Wronskian解和Grammian解. (3-6) 将(3-6)代入(3-5),用平衡法求得:m为任意正整数,n1=3,n2=0. 令 φj,t=αφj,xxx,φj,y=βφj,mx, (3-7) 当m=1时, φj,t=α1φj,xxx,φj,y=β1φj,x. (3-8) 由-3β1-β1-pα1β1=0得,pα1β1=-4β1,上式计算为 所得结果用Maya图表表示为 结果为行列式的Plücker关系式.当m=1时,(2-4)在(3-8)的条件下,且pα1=-4时,为(3-5)的Wronskian解. Wronskian可用Pfaff式表示为Wr(φ1,φ2,…,φn)=(d0,d1,d2,…,dN-1,1,2,…,N).其中, 由(2-6)同理设 φi,y=a1φi,x,φi,t=b1φi,xxx,ψj,y=a1ψj,x,ψj,t=b1ψj,xxx. (3-9) 将Grammian用Pfaff式表示,基于(2-7)式,求τ关于x,y,t的各阶导数,代入(3-5)得 由-4a1-pa1b1=0,得-4=pb1时,有 所得结果与BLMP方程的Grammian解都为Jacobi恒等式,只相差系数,Maya图相同.故在(3-9)的条件下,且-4=pb1时,(2-7)为(3-5)的Grammian 解. 相对行列式,Pfaff式的性质人们了解的很少,但是Pfaff式的性质比行列式更丰富.本文基于双线性方法得到方程的Wronskian解时,双线性方程结果化为Plücker关系式,求Grammian解时双线性方程化为Jacobi恒等式,通过其Maya图表不难发现,这两种行列式的恒等式只是Pfaff式恒等式的特殊情形: 文中还利用双线性形式的倒推得到了一个变系数的BLMP方程,采用平衡法可构造Wronskian解.Pfaff式的广泛应用、平衡法以及这种倒推方法也可以在其他方程中进行考虑. 致谢本工作受到河南省研究生教育优质课程、河南省大学生创新创业计划项目、理学院教研项目的支持资助,在此表示感谢.2.2 BLMP方程的Grammian解


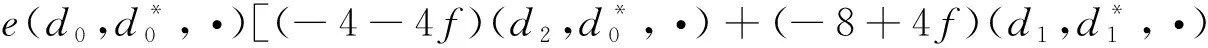

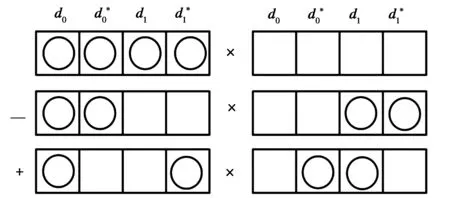
3 变系数BLMP方程的精确解
3.1 变系数BLMP方程的Wronskian解

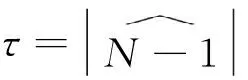

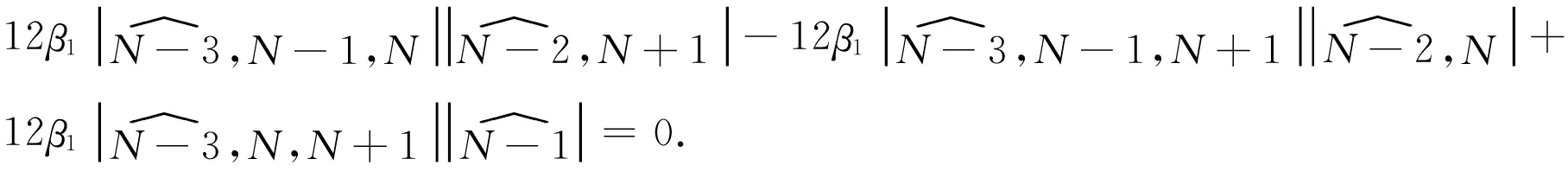
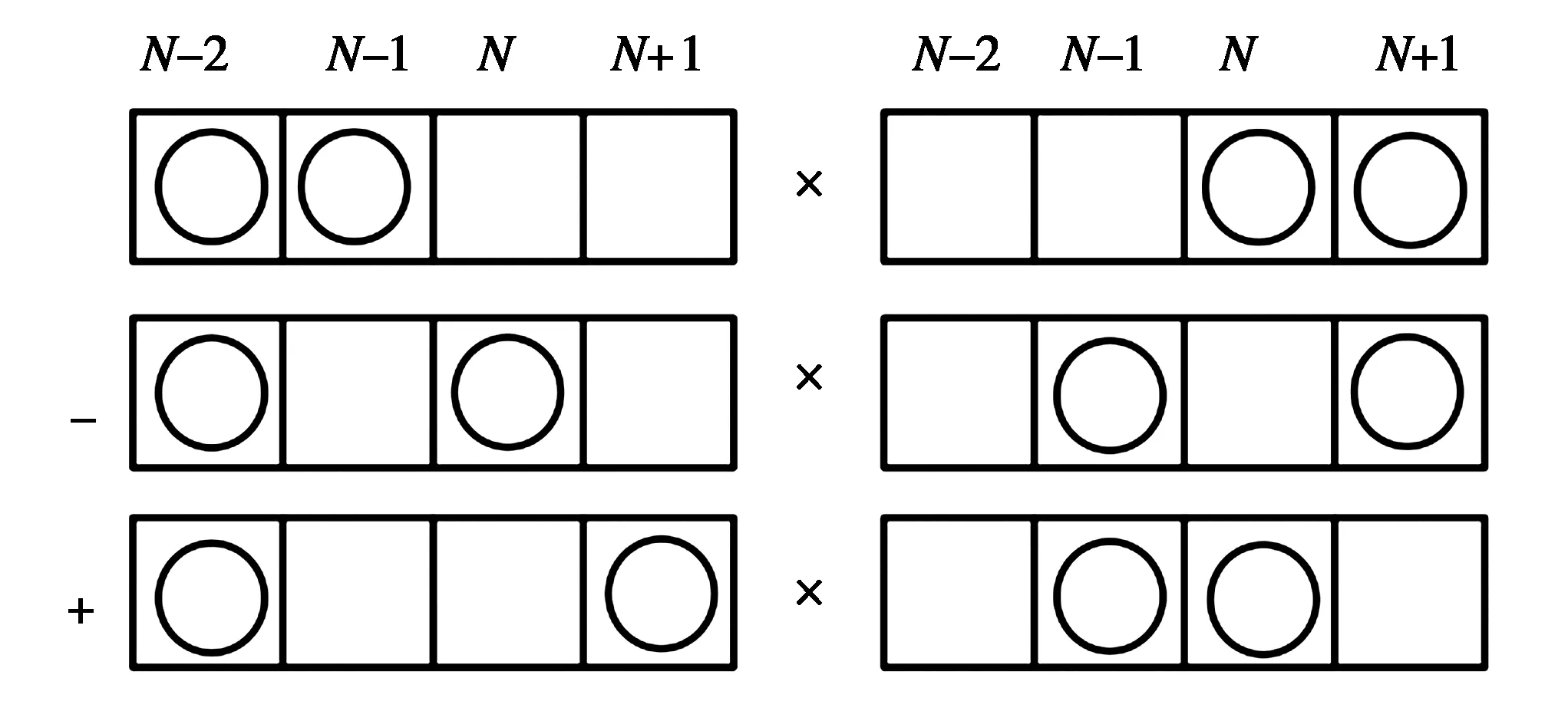
3.2 变系数BLMP方程的Grammian解


4 结论


