变系数Hirota方程的相互作用研究
史磊 吴坤

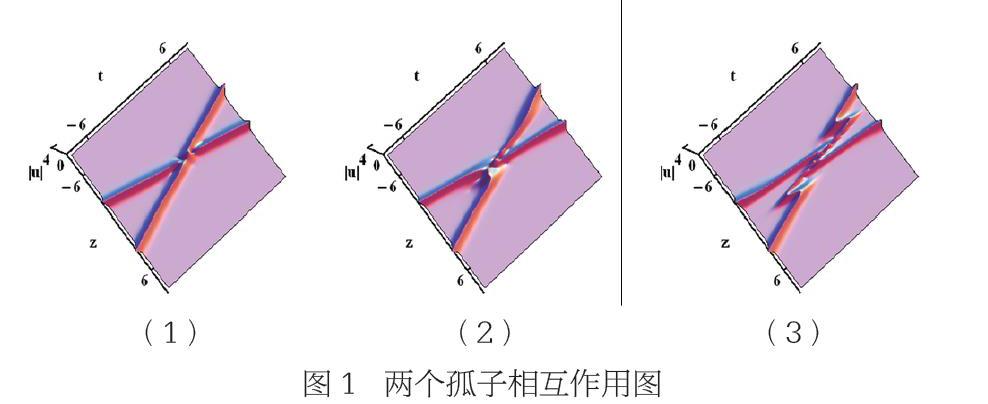
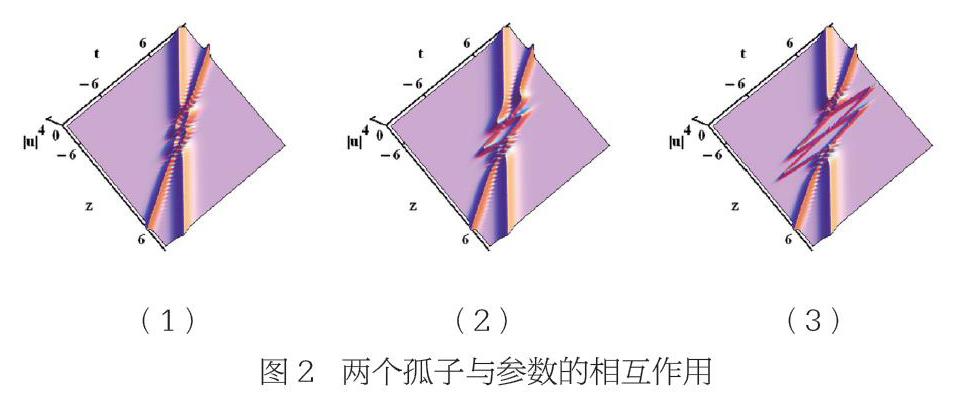
【摘 要】 本文研究了变系数Hirota方程的孤子相互作用,可用于表征非线性光纤通信的孤子。利用双线性方法和符号计算,得到了变系数Hirota方程的两个孤子解。基于孤子解,通过分别选择三阶色散和一阶色散项的不同值来显示孤子相互作用的新现象,最终研究结果表明,随着参数的增大,孤子相互作用的范围以及形状会更加增大和复杂。
【关鍵词】 Hirota方程;孤子相互作用
非线性薛定谔(NLS)方程是一种具有孤子解的非线性演化方程,可以描述非线性光纤通信中的群速度色散(GVD)和自相位调制(SPM)之间的平衡引起的孤子。孤子是孤立波,它在相互作用后保持其速度和形状,故孤子可被认作准粒子。另一方面,孤子相互作用是非线性光纤通信中的一种特殊现象,由于相互作用,孤子在传播中相互影响,导致传输速率严重衰减。因此,研究孤子相互作用并找到一种有效的控制方法尤为重要和迫切。事实上,孤子相互作用可以通过三阶色散(TOD)项来减少,它主要集中在两个孤子上。
【参考文献】
[1]M.J.Ablowitz and P.A.Clarkson.Solitons,nonlinear evolution equations and inverse scattering,Cambridge Univ.Press,Cambridge(1991).
[2]V.B.Matveev and M.A.Salle.Darboux transfoemations and solitons,Springer, Berlin(1991).
[3]R.Hirota,The direct method in soliton theory,Cambridge Univ.Press, Cambridge(2004).
[4]A.Chabchoub,N.P.Ho mann and N. Akhmediev.Rogue wave observation in a water wave tank,Phys.Rev.Lett.106,204502(2011).

