西宁市高中生数列CPFS结构的实证分析研究

王 煜，李佳鑫

(青海师范大学数学与统计学院，青海西宁 810008)

1 问题的提出

数列素养(Sequence literacy)是大数据背景下数学素养的重要方面，在新课标(《普通高中数学课程标准(2017年版)》)下数列作为一类能解决实际应用问题的特殊函数，被编排在选择性必修课程中的函数主题一栏，该选择性必修课程中包含函数、几何与代数、概率与统计、数学建模活动与数学探究活动这四个主题[1].函数作为高中数学学习的重点与难点，函数思想贯穿于整个高中数学中，而数列位于函数主题中，可见数列在高中数学中占有重要地位[2].所以提升学生的数列素养，可以有效地帮助他们分析和解决日常生活中简单的实际数学问题.

数列知识认知结构的构成、发展和完善的整个过程[3]，就是学生学习数列知识的实质.对于认知结构而言，喻平教授创造性地提出了数学学科特有的认知结构——个体的CPFS结构[3，4].在认识CPFS结构前，我们首先要了解什么是图式？图式是命题或相似事物的知觉特征的编码形式，它是将观念按属性组合的知识储存方式[5].南京师范大学的喻平教授在多年教学实践的基础上，通过大量实证研究，以数学学习心理理论框架为基础，提出概念域、概念系、命题域和命题系四个理论[6]，这四部分形成一种数学学习特有的认知结构，随后将该认知结构取其英文首字母命名为CPFS结构[7].并于2003年提出：一切与数学概念C等价解释的图式称作概念C的概念域[8]；和概念域相似的是，一个典型命题A的命题域称作一个等价命题网络的图式；一组具有数学强、弱、广义抽象关系的概念网络图式，称为概念系[9]；而定义命题系的是一个命题集的图式，其中被包含于这个命题集里的任何一个命题存在着至少与另外一个命题有广义抽象中的前后关联关系[10].

本研究将CPFS结构作为理论基底，对西宁市某中学高一到高三年级学生的数列认知进行实证研究.分析该中学高中生的数列CPFS结构整体水平如何？而年级与性别的差别是否会是影响学生的数列CPFS结构的因素呢？若有影响，是怎样影响的呢？

2 研究问题

(1)西宁市高中生个体数列CPFS结构优良性整体水平分析;

(2)西宁市高中生数列CPFS结构不同年级差异分析;

(3)西宁市高中生数列CPFS结构不同性别差异分析.

3 研究设计

3.1 问卷

为了有效地考察学生数列CPFS结构的认知情况，问卷参考了喻平教授在其博士论文《数学问题解决认知模式及教学理论研究》中提到的目标回忆、结点连线、辨证推理、等价推理和命题应用这五种检测CPFS结构的方法.编制出了适用于本研究的问卷，其各题目题干如下：

(1)写出数列的概念，并阐述出你所理解的数列.(将你能想到的与数列相关的知识都陈述出来，比如数列的分类、特点、性质等等)

(2)联想曾经所学的数学知识点，在A、B、C、D、E、F、G这7个选项中选出与数列知识相关的选项，且分析出你的理由，陈述数列与你所选选项知识间的联系.A.等式；B.不等式；C.函数；D.方程组；E.三角函数；F.代数式；G.递推.

(3)若数列{an}是等差数列，2a5=a3+a7是否成立？2a5=a1+a9呢？为什么？ 2an=an-1+an+1(n>1)是否成立？据此你能得出什么结论？2an=an-k+an+k(n>k>0) 是否成立？据此你能得出什么结论？

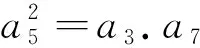
(4)由等差数列通项公式an=a1+(n-1)d、等比数列通项公式an=a1.qn-1出发，你可以推出哪些能代表是等差、等比数列的公式？尽可能地写出你能想到的公式，并写出关键的推导思路.

(5)在数列的学习过程中，你学到了哪些数学方法或是数学思想？

(6)请自行编制出一道有关数列知识的题目，并写出解答该题目的主要思维路线.

3.2 被试对象

本文选取西宁市某中学280名高一到高三年级学生参与了此次测试，其中3个年级分别随机抽取2个班进行测试.本研究共发放280份测试卷，去除42份无效卷，回收有效卷共238份，其中高一、高二及高三年级被试有效人数分别为82名、70名及86名，且这238份有效卷中男生121人，女生117人.

3.3 方法

本文运用统计软件SPSS20.0对测试数据结果进行统计性分析.需要指出的是，笔者通过SPSS20.0对本研究测试卷进行了信、效度的检验，检测到问卷信度系数达到0.773>0.7，效度KMO值为0.81>0.7，并且该问卷Bartlett球形度检验出的P值(Sig.)为0.000<0.05，说明问卷的可信度较高，效度也良好，即本文所编制的问卷具有良好的信度、效度，其调查数据可以为本研究所用.

4 结果分析

4.1 高中生个体CPFS结构优良性的整体分布情况

笔者对本研究收回的238份有效问卷的数据进行了整理，得到高一、高二及高三三个年级学生的数列CPFS 结构测试成绩结果(该问卷分数越高则说明被试建构的数列CPFS结构越好).对其进行描述统计，结果如表1所示.

表1 238名被试的数列CPFS测试结果统计

由表1中数据可知：238名学生CPFS测试成绩的最高分为34分，最低3分，明显看出最高与最低相差很大，其平均值M为16.91，标准差δ为6.5，同样相差很大；同时从表1可看出结果的偏度系数是0.061，即学生分数位于平均分左右的居多，由此可以得到这238名被试的数列CPFS结构认知情况整体一般.

同时笔者还得出了被试高中生的数列CPFS结构正态曲线，如图1所示.

图1 高中生数列CPFS结构正态曲线

由图1成绩正态曲线可以得到：不同学生间的数列CPFS结构存在较大的不同，在中、高分区间差距更大.

利用均值M和标准差δ，将这238名被试按 CPFS 测试成绩的不同分为三组(M+δ和M-δ均四舍五入取整)：“低CPFS结构”组分数为0到10分(包括0分和10分)；“中CPFS结构”组分数为11到23分(包括11分和23分)；分数高于23的均为“高CPFS结构”组.每组人数及具体的所占比如表2所示.

表2 238名被试的数列CPFS结构的总体分布

通过观察表2，得到：被试中有34人(14.29%)的数列CPFS结构较好，157人(65.96%)数列CPFS不太完善，而47人(19.75%)并未建立良好的数列CPFS结构.

4.2 年级对数列 CPFS 结构的差异性研究

笔者通过SPSS软件分析出三个年级被试的数列CPFS结构测试成绩的描述性特征，结果见表3所示.

表3 各年级被试数列CPFS结构测试成绩的描述统计量

续表

从表3分析各年级总分均值情况可看出：被试的数列CPFS结构的完善程度为高三>高一>高二.具体而言，从表3中数据可以比较学生的数列CPFS结构测试成绩的标准差，其结果显示高二年级最高，高三最低，说明针对学生的数列CPFS结构，高三年级最稳定，高一次之，而高二被试最不稳定.

但是不同年级CPFS结构测试成绩均值的不同并不能说明该年级学生个体是否普遍最高或者最低，或者说CPFS结构水平是否真的是高三>高一>高二.因此笔者首先得到了各年级总人数百分比(如表4)、各年级学生数列 CPFS结构各等级所占百分比(如表5)，其次应用方差分析(ANOVA)法对三者做了差异性分析，结果如表6、表7和表8所示.

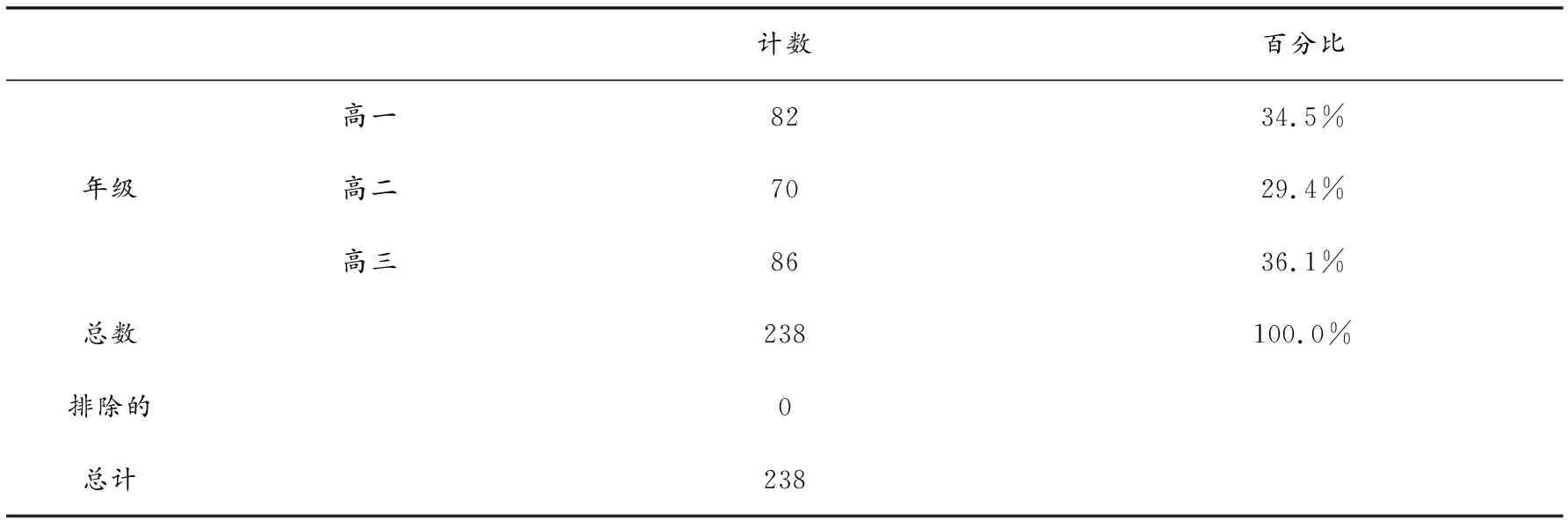
表4 各年级总人数所占百分比

表5 三个年级被试的数列CPFS结构低、中、高所占百分比

Levene方差齐性检验结果如表6所示.

表6 年级对测试结果的Levene方差齐性检验

观察表6中数据：其Levene统计量对应的p>0.05，所以得到各年级对CPFS结构测试的成绩满足方差齐性的结论.

各年级对CPFS结构测试成绩的单因素方差分析结果，如表7所示.

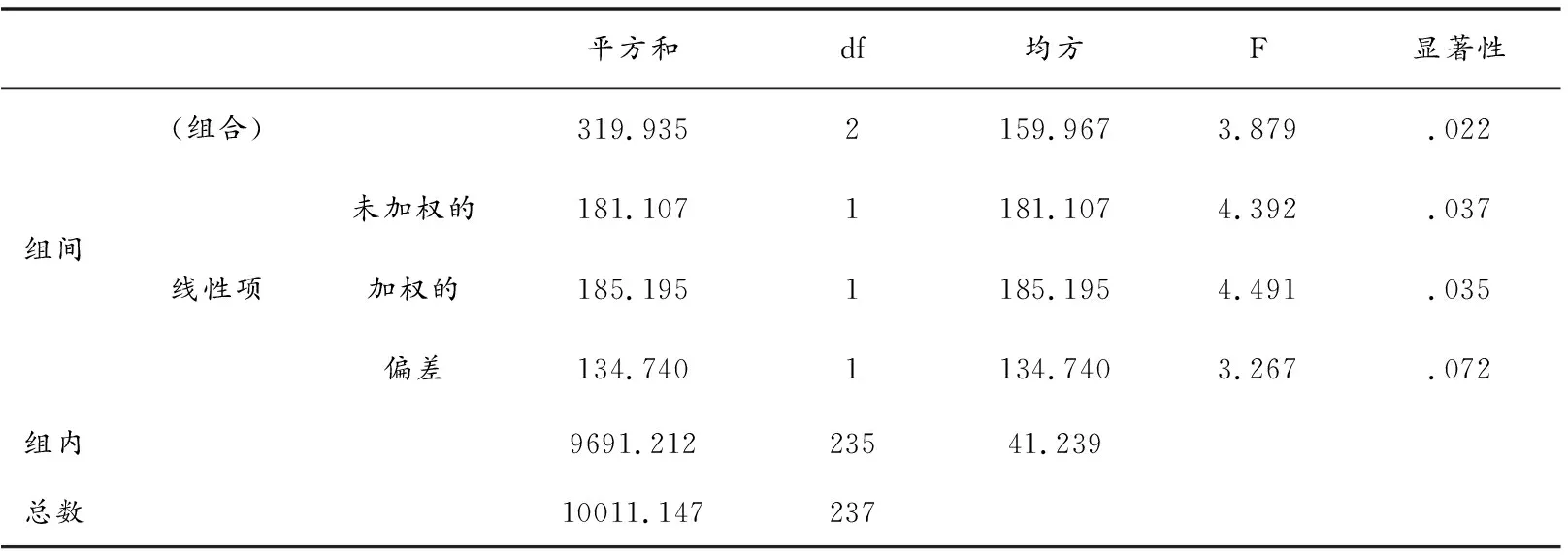
表7 各年级对数列CPFS结构测试成绩的单因素方差分析结果

观察表7得到数据：p=0.022<0.05，所以结果拒绝原假设，也就是说，不同年级被试的数列CPFS结构测试成绩并不完全相同.

然而拒绝单因素方差分析原假设并不能得出各年级间数列CPFS结构测试成绩均值完全不等的结论.还得通过多重比较检验结果进行各年级间数列CPFS结构测试成绩均值的两两比较，如表8所示.

表8 各年级间数列CPFS结构测试成绩的多重比较检验结果分析

由于表6得出结果方差满足齐性，表中的均值差又给出了不同年级间数列CPFS结构测试成绩的均值之差，可以看出高一和高三、高二和高三年级间的数列CPFS结构测试成绩存在显著差异，而高二和高一年级间的差别不明显.此结论由表8中显著性列给出的p值大小与0.05比较(p>0.05不显著，p<0.05显著)也可得出.

综上所述，年级会影响学生数列CPFS结构的认知.

4.3 性别对数列 CPFS 结构的差异性研究

笔者还用SPSS20.0软件将性别作为变量，分析出了被试男、女的数列CPFS结构描述性特征，具体见表9.

表9 男、女被试的数列CPFS结构成绩描述统计

从表9中数据可以得到：从数列CPFS结构测试成绩的标准差来看，被试女生的标准差略低于被试男生，说明与被试男生相比，被试女生的数列CPFS结构要更稳定一些；而从均值来看，结果中被试男生和女生的数列CPFS结构测试成绩的平均值相差不多，也就是说，当被试对象的性别不同时，被试的数列CPFS结构不会有显著差异.

由表9中比较男、女被试数列CPFS结构测试成绩的均值与标准差还不能说明结果的普遍性，因此笔者对男女生的CPFS结构做了差异性分析，结果如表10和表11，其中运用到两独立样本t检验与方差分析这两种方法.

表10 被试男女生的CPFS结构独立样本t检验

由上表10可知，其Levene’s方差齐性检验的p值结果是0.769>0.05，说明男生和女生数列CPFS结构测试成绩的方差满足齐性(Levene’s方差检验的原假设是方差满足齐性)，所以t检验结果应该看表10的假设方差相等行.结果显示t检验的p值为0.926>0.05，说明男女生的数列CPFS结构成绩的方差无明显差异.

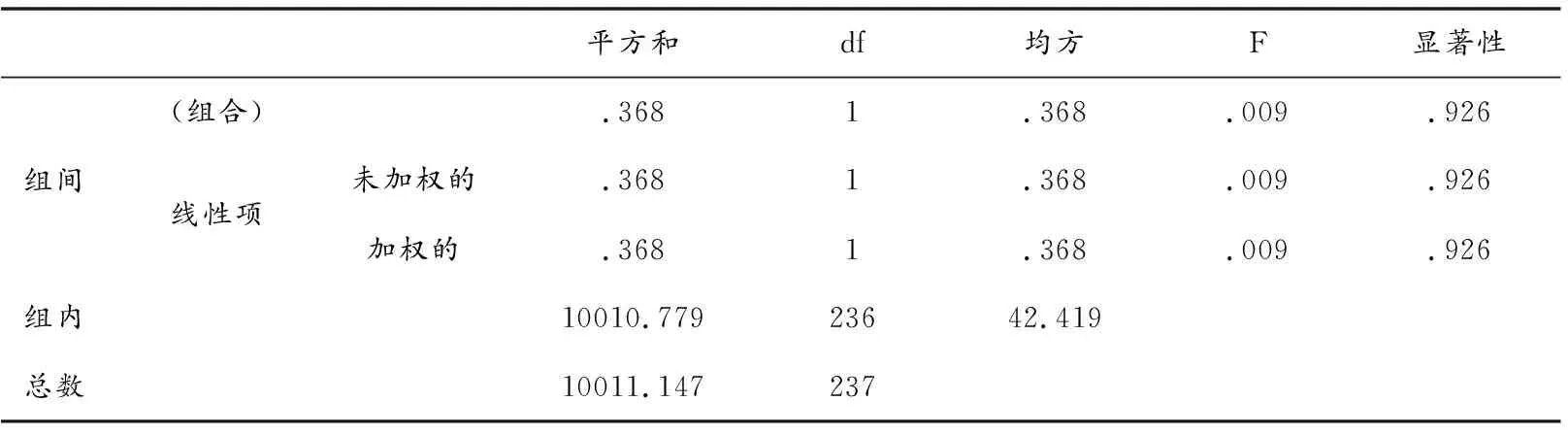
表11 被试男女生CPFS结构的单因素方差分析结果

根据表11的组间方差检验的结果可知，其显著性水平为0.926>0.05，说明238名学生中男、女性别的不同对其数列CPFS结构的影响并不显著，即性别并不会影响学生的数列CPFS结构.

5 结论

经数据统计及SPSS20.0数据分析，对西宁市某中学高一到高三年级学生的数列CPFS认知结构分析，可得如下结论：

(1)238名高一到高三学生建构的数列CPFS结构整体水平一般，且个体间的数列认知差距较大.具体而言，高CPFS结构组占14.29%，低CPFS结构组占19.75%，中CPFS结构组占65.96%.

(2)年级会影响学生的数列CPFS结构.随着学生年级的不同，学生所建构的数列CPFS结构的稳定性和完善程度都不同，且年级间的差异均为高三>高一>高二.

(3)238名学生中男、女性别的不同对其数列CPFS结构的影响并不显著，即性别并不会影响学生的数列CPFS结构.