分子系统发育分析中的物种选择规则

李可群

(同济大学化学科学与工程学院，上海 200092)

自达尔文时代起，许多生物学家都有一个梦想，那便是重建地球上所有生命的进化历史并以进化系统树的形式描述这部历史[1].研究物种进化的理想途径是利用物种的化石证据，但是自然界中化石存留下来的比较少，很多进化的关键环节都没有化石证据存留.因此大多数生物是通过比较形态学和比较生理学构建生物进化史的框架，然而形态和生理状态的进化相当复杂，不同学者构建的进化系统树在细节上有所差别，得出的物种进化关系难以统一[2].近年来，随着分子生物学研究的不断深入，大大改变了这种局面.不过，目前分子系统发育分析在计算物种分歧时间时，大多基于分子进化速率恒定的“分子钟”假说[3]，但大多数生物分子在长时间尺度和不同谱系的进化速率并不恒定，从而计算得到的结果与化石年龄往往存在较大偏差.如原口动物和后口动物分歧时间化石给出的年代大约在5.55亿～5.60亿年前，而近年来快速发展的生物分子钟方法推算结果大多介于12亿～8.51亿年前，仅有极少数给出小于6亿年前的结果，即几乎所有分子钟研究结果显示两者分异早于寒武纪生物大爆发至少1亿年[4].为此本文作者提出了不基于分子进化速率恒定假说的分子绝对进化速率计算公式[5]和多重突变的校正方法[6]，本文将继续讨论分子系统发育分析中的物种选择规则.

1 基本原理

1.1 分子进化与泊松分布

根据分子进化模型[6]，由于突变概率很低，核苷酸或蛋白质序列分子的突变概率可用泊松分布来描述

(1)

式(1)中k为分子绝对进化速率，t为进化时间，p(x=j)为突变j次的概率.特别地，核苷酸或蛋白质序列分子不发生突变的突变概率为

p(x=0)=e-kt

(2)

对于一个有n0个被比较位点的核苷酸或蛋白质序列分子，若忽略回复突变(可校正，参看文献[6])，有

(3)

式(3)中nd为核苷酸或蛋白质序列分子相对于其被比较的祖先核苷酸或蛋白质序列分子发生突变的位点数，p为这两个序列分子的序列差异率，kt一项称遗传距离.

1.2 物种选择的一般原理

由于祖先序列分子一般难以得到，实际工作中我们一般通过比较同源序列分子来计算物种分歧时间.根据文献[5]，两个同源序列分子比较得到的序列差异率可表示为

(4)

(5)

文献[5]指出当两个遗传距离kAt和kBt存在一定差异但相差不十分悬殊时，式(5)得到的分子绝对进化速率是其真实值[即式(4)的对应值]的2倍.但替代公式的使用会带来误差，其差值为

(6)

因此，分子系统发育分析中物种选择规则的实质就是使替代公式在物种分歧时间计算时引入的总体误差取最小值，否则最优化计算过程中式(5)得到的绝对进化速率将偏离为其真实值2倍的关系，同时会给出错误的物种分歧时间结果.若不考虑式(4)的误差，此亦即使用式(5)进行物种分歧时间计算的总体误差.

1.3 计算体系中同组同源序列分子的平均未突变概率

在分子系统发育分析中，我们一般使用两组同源序列分子相互两两比较.在成功的计算体系中，我们发现它们的同组同源序列分子平均未突变概率存在一些规律.我们以文献[7]使用COX1蛋白质分子计算寒武纪生物大爆发时期原口动物与后口动物分歧时间为例，文章分别使用一组鲨鱼和一组环节动物作为物种类群A和物种类群B，另外选用了腕足动物、轮虫动物、线虫动物、节肢动物和软体动物分别作为物种类群C，参见图1.文献[7]的计算表明：所得的原口动物与后口动物物种分歧时间数值很相近，且与化石年龄相符很好，远好于现有文献结果，说明计算结果令人满意.

图1 寒武纪物种分歧时间的计算框图

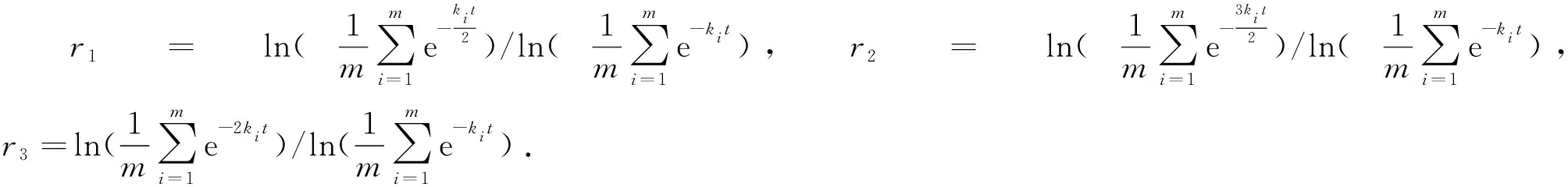
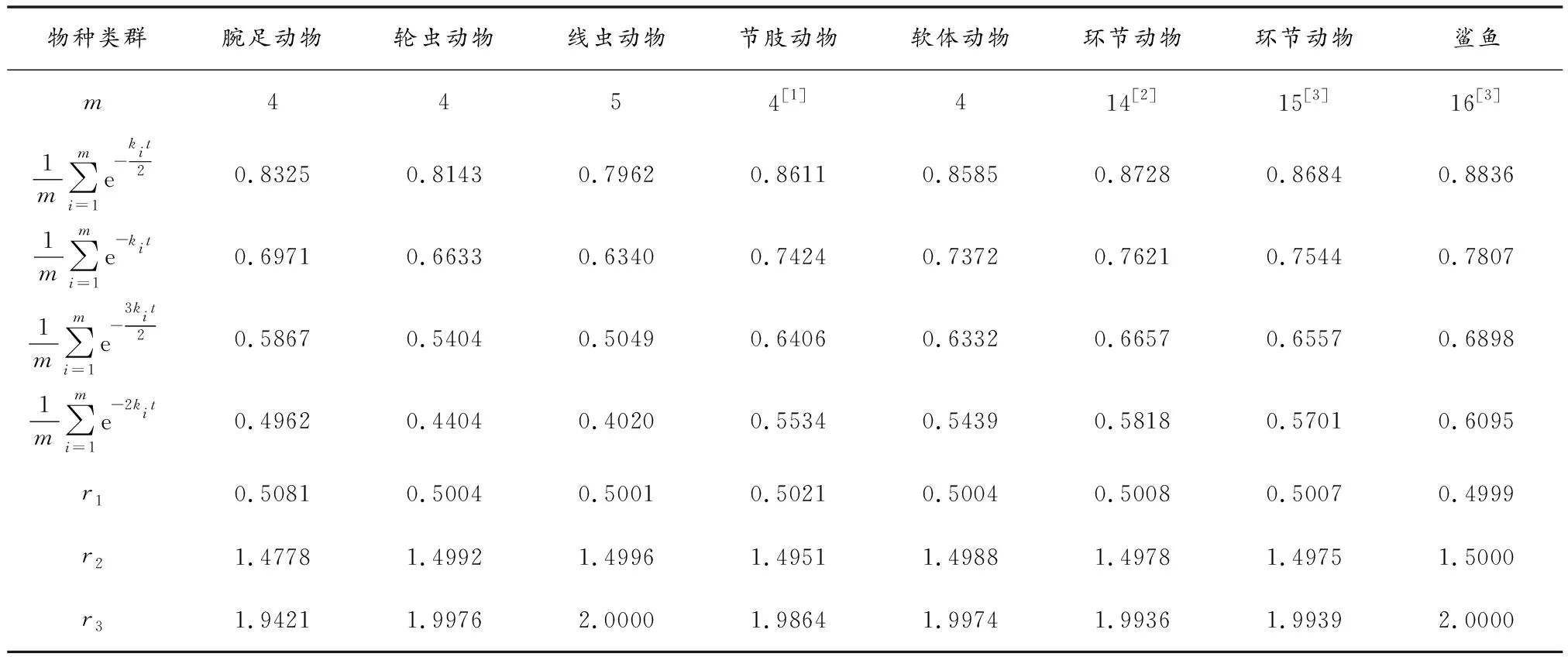
表1 寒武纪物种分歧时间计算中同组同源序列分子的平均未突变概率

由表1可以看出，当同组同源序列分子的遗传距离取kit的倍数时，其对应的平均未突变概率取自然对数后的比值r等于它们倍数，即如果我们令

(7)

那么就有

(8)

式(8)中c为0.5、1.0、1.5和2.0.我们随意以表1中软体动物类群为例，试图对式(8)做出解释，表1中其他动物类群计算结果与之相同.

表2 软体动物的平均未突变概率

表2中给出了寒武纪物种分歧时间计算时，软体动物不同物种e-ckit的数值.可以看出，它们与其同组物种式(8)均值e-ckxt的相对偏差的加和均为零，且同一软体动物物种不同c值时的相对偏差数值的比值与它们c值的比值相同.也就是说，如果我们把e-kit理解为e-kxt与多出部分的乘积，即

e-kit=e-kxte-Δkit

(9)

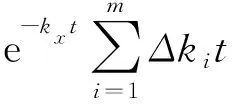
2 分子系统发育分析中的物种选择规则

2.1 两物种类群体系

两物种类群体系由两种物种类群(即一个物种类群对)的物种序列分子相互两两比较计算的物种类群对组成.虽然两物种类群体系在我们的分子系统发育分析中并不常用，但它是一个较为基本的类型，因为常见的三物种类群体系和四物种类群体系分别由3个和6个物种类群对组成.

如果kA(i)和kB(j)分别为物种类群A的第i个物种和物种类群B中第j个物种的序列分子绝对进化速率，t为两物种类群的分歧时间，则替代公式引入总体误差取最小值的目标函数是

(10)

式(10)较难直接求解.但若物种类群A和B序列分子的平均未突变概率均满足式(8)，则问题可以简化.我们令

(11)

s′=(e-xA-e-xB)4

(12)

使用式(12)中的s′分别对xA和xB求一阶偏导数并令它们为零.不难得到式(12)取最小值的条件为e-xA=e-xB，即物种类群A和B序列分子的平均未突变概率相等.

2.2 三物种类群体系

2.2.1 三物种类群体系物种选择规则

由图1计算框图可以看出，三物种类群体系由3个相互两两比较计算的物种类群对组成.因此我们可得到替代公式引入总体误差取最小值，也就是物种选择规则的目标函数为

(13)

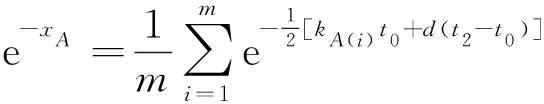
(14)

(15)

由多元函数的极值条件，式将(15)中的s′分别对xA、xB和xC求一阶偏导数并令它们等于零，有

(16)

(17)

(18)

由式(16)至式(18)可以看出，其中任意两个方程的加减可得到第三个方程，故其中任意两个方程均为式(15)的多元函数极值条件.以式(16)和式(17)为例，存在两组解：

(1)e-xA=fe-xB=fe-xC，即图1计算框图中物种类群B和C的序列分子自它们最近共同祖先序列分子的平均未突变概率相等；同时，自时间t2起物种类群A、B和C的序列分子的平均未突变概率也相等.换句话说，也就是图1中3个物种类群对两两相互比较计算时残差分别取最小值，这时三物种类群体系的总残差也取最小值.

(2)因x3-y3=(x-y)(x2+xy+y2)，故若使式(16)有解，可有

(19)

将式(19)转换定义为

(20)

同样地，由式(17)可有

(21)

不难看出，式(16)和式(17)成立时，式(20)和式(21)中R1和R2值均为1.

2.2.2 物种选择规则的验证

我们使用1.3引用的寒武纪物种分歧时间计算结果来验证物种选择规则.表3给出了选用不同物种类群C时计算体系R1和R2的计算值.

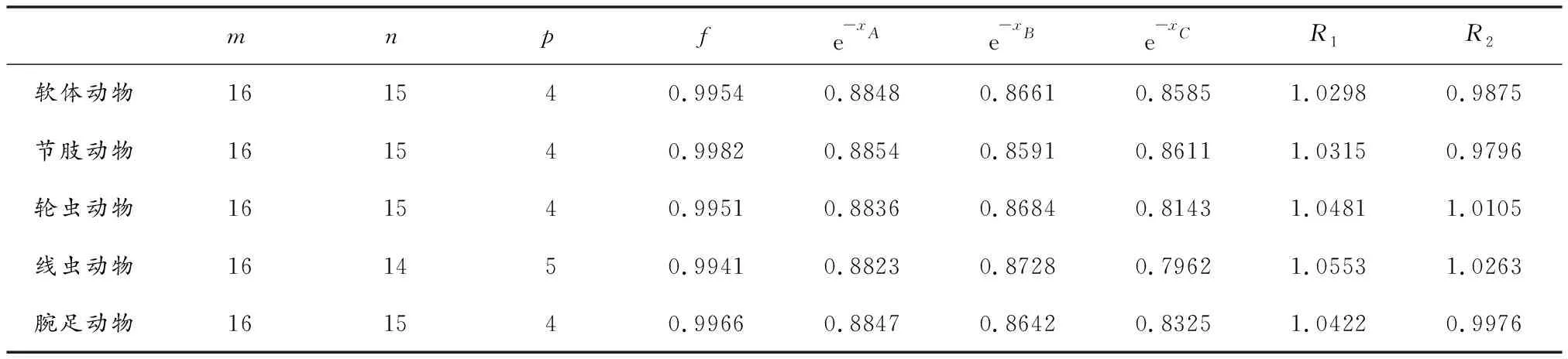
表3 寒武纪物种分歧时间计算时物种选择规则的验证

由表3可以看出，不同物种类群C计算所得的R1和R2值均很接近于1，说明我们所选择的物种符合物种选择规则的要求，因而能得到满意的结果.另由表1数据可以看出这些物种类群满足式(8)的要求.

2.3 四物种类群体系

四物种类群体系的计算框图如图2所示.

图2 四物种类群体系物种选择规则的推导示意图

按三物种类群体系类似的方法，我们可以得到四物种类群体系物种选择规则的目标函数为

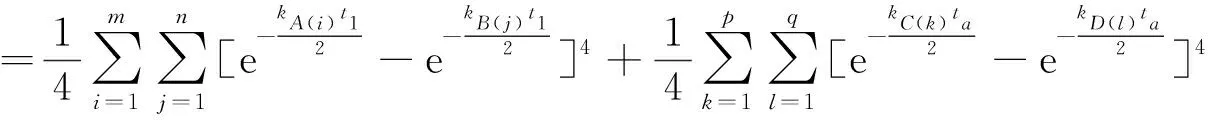
(22)

(23)

(24)

根据多元函数的极值条件，将式(24)分别对xA、xB、xC和xD求一阶偏导数并令为零，有

(25)

(26)

(27)

(28)

式(25)至式(28)方程组的解有两类：

(1)由式(25)至式(28)可先直观得到e-xA=e-xB，e-xC=e-xD，也就是物种类群A与物种类群B各物种的序列分子，物种类群C与物种类群D各物种的序列分子自它们各自最近共同祖先序列分子的平均未突变概率分别相等.同时还可推断出从时间t2开始的四个物种类群各物种序列分子的平均未突变概率也分别相等.与三物种类群体系2.2.1(1)中的情形类似，也就是组成四物种类群体系所有物种类群对的残差分别取最小值.

(2)由于式(25)加式(26)、以及式(28)减式(27)的结果相等，两个结果中任意一个方程式都包含了式(25)至式(28)的解，因其还可能存在其他解，根据下面的结果选择出的物种组成是否满足式(24)的极值条件，还需结合化石年龄等其他学科证据进行了判断.以式(25)加式(26)为例，两边除以g后其结果为

(29)

整理后可得

(30)

同样地，式(30)较难直接求解，我们讨论其中较简单的情形.因x3-y3=(x-y)(x2+xy+y2)，因此式(30)要有解，可让其方程式两边均能提出等于零的因式.即有

(31)

(32)

将式(31)和式(32)整理可得判别式

(33)

(34)

式(29)的其他类似组合还可得到另外两组解.

由本文三物种类群体系和四物种类群体系分析可知，它们的物种选择规则可分成2类：第一类直接让组成上述2类体系所有物种类群对的残差取最小值，即让后者物种类群平均未突变概率分别相等。另一类是允许体系中物种类群对的平均未突变概率存在差异，而这些差异可在由多元函数极值条件得到的方程组中相互抵消，仍满足相关极值条件.如式(20)和式(21)以及式(33)和式(34)等都是通过这种方法得到的.同时，由前面分析可以看出，无论两物种类群体系、三物种类群体系或四物种类群体系，由于变量较多，它们通过多元函数极值条件得到的方程组通常较难直接求解.而选用均满足式(8)的物种类群，尽管可能不能穷尽其解，但可以非常方便地找到其中方程组的简单解，也就是能简单方便地找到可计算得到满意物种分歧时间的物种类群组成，这对我们的分子系统发育分析是很重要的.我们在实际计算中也发现，大多数成功的计算体系是由其同源序列分子满足式(8)的物种类群组成.

最后需要说明的是，由文献[6]的回复突变和平行突变校正方法可知，本文结果也同样适用于同源分子绝对进化速率计算公式经多重突变校正的分子系统发育分析体系.