计算行列式的几种不同方法解析
全彤 浙江农林大学暨阳学院商学院 帅昌浩 浙江农林大学暨阳学院工程技术学院
一、预备知识
1.行列式相关定义:
(1)上三角(形)行列式与下三角(形)行列式
上三角(形)行列式:形如的行列式。
(2)对角行列式与副对角行列式
(3)余子式与代数余子式
2.行列式的特点与性质:
(1)行列式与它的转置行列式的值相等.
(2)互换行列式的两行(列),行列式变号.
(3)若行列式有两行(列)相同,则行列式为0.
(4)行列式某一行(列)的公因子可以提到行列式符号外面.
(5)若行列式的某一行(列)是两组数的和,则此行列式就等于两个行列式的和.这两个行列式的这一行(列)的元素分别为对应的两数之一,其余各行(列)元素与原行列式相同。
二、行列式计算主要方法
1:利用基本公式计算
(1)范德蒙德行列式求解
解题思路:这是一个范德蒙德行列式,本题可直接套用范德蒙德行列式公式求解,即
(2)特殊行列式的计算:
解题思路:这是一个下三角行列式,可直接利用三角形行列式的计算公式得到结果,其值等于主对角线上各个元素的乘积。从而
2:利用分块矩阵来计算行列式
解题思路:解法1:看到这道题,我的第一想法是把四阶行列式化为四个分块矩阵的形式,不妨令,则原四阶行列式可表示为,此时行列式看起来就更显简洁明了了。
这种解法虽然最终答案与标准答案相符,但是由于定理要求A是可逆的,即要求A 的行列式不等于0,而题目中,题中未说明a 具体的值,即a 是否等于0 未知,所以此解法仍有失严谨,需要分类讨论来计算。
为使解题过程更加严谨,不妨可以采用行列式展开定理求此题。由行列式的展开定理得到:

行列式展开定理省去了对a 的值的讨论,显得比较方便。
3:降阶法
解题思路:对于低阶行列式(三、四阶)直接用降解法是来求行列式是比较方便的。由于此三阶行列式第二行含有三个相同的数1,则可先通过列初等变换将第二行的两个元素化为0,即C2-C1,C3-C1,得到由此可根据行列式展开
解题思路:由于此四阶行列式每一行所有元素相加之和相同,所以考虑将2,3,4 列元素加到第1 列,由此第一列所有元素等于,于是可以提取公因式 ,第一列所有元素均变为1,然后就可以根据行初等变换将第一列中的三个元素变为0,这时通过行列式的展开定理就可以更方便地计算行列式的值了,本例中将第一列展开,此时的行列式降阶为三阶行列式,这时的三阶行列式就更容易求了,可以继续降阶为二阶行列式,即易得答案。
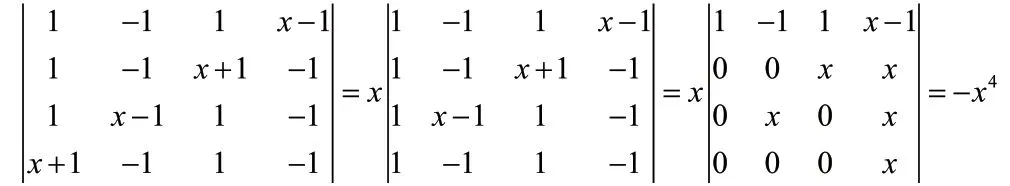
4:升阶法/加边法
解题思路:观察此行列式可得出在计算前在行列式上加上恰当的一行或一列可保持行列式的值不变,而且可以使计算简化。

5:利用行列式性质(通常较广泛地应用于抽象行列式)
解题思路:
第一步:根据行列式的基本性质2:互换行列式的两行(列),行列式变号。可由
第二步:根据行列式的基本性质5:若行列式的某一行(列)是两组数的和,则此行列式就等于两个行列式的和。故,
解题思路:B 中第一列元素都表示为两个数的和,根据性质可将B 拆分成两个行列式来求,其中一个行列式两列相同行列式为零,简化了计算。

本题也可以用分解的方法来解,将矩阵分解成两个矩阵的乘积。

6:数学归纳法求n 阶行列式
解题思路:观察可以得到本题中四个行列式有一个共同的特征,即主对角线上的元素和除主对角线外的所有元素分别都相同,即主对角线元素都为1,除主对角线外的元素都为2。由此可思考这四个题目之间的联系,试用数学归纳法出发对本题进行分析:
用数学归纳法来证明

由假设得:

由此就可得到诸如此类的行列式的n 阶行列式的计算公式。在例9 中,相当于取,可得:
7:利用因式定理法
解题思路:先把第2 列到第n 列元素都加到第1 列上去,第1 列元素都相同

利用因式定理法的行列式的特征:这类行列式一般是含有文字变量的行列式,当某个变量取某个特定值时行列式的值为0,则该行列式必定含有某个特定因子。
因式定理法的解题步骤:利用行列式的性质找出行列式的所有因式,因此得到行列式的值,利用行列式的定义的展开式观察行列式展开式(多项式)的特征,如果次数与找到的所有因式的乘积的次数相同,就利用展开式的首项系数对因式乘积的系数进行相应调整,就可以得到行列式的值了。
三、总结
行列式是线性代数的重要内容,行列式的计算是行列式这一章的重点和难点,由于行列式类型的多样性,不同类型的行列式其计算方法也不尽相同,同时有些题目可以有不同的计算方法。本人作为学生,认识和理解水平有限,本文只是针对最常见的特殊行列式的计算方法展开讨论,归纳总结了七种方法,希望这些计算方法对学习行列式的学生有所帮助。

