车辆跟驰模型稳定的充分必要条件

韩祥临，欧 桥，王心宇,瓦 米

(湖州师范学院 理学院，浙江 湖州 313000)

0 引 言

交通流的稳定性是目前交通流研究的热点[1-8].Bando等[9]考虑了如下情形：在长度为L的圆形道路上有N(N≥2)辆车，假设每辆车有一个优化速度V，它只依赖当前车与其前车的车头间距Δxn(t)=xn-1-xn=hn(t)，其中xn为第n辆车的位置.文献[9]提出了优化速度模型：

(1)

其中，a>0为常数，表示当前车司机的敏感系数.

文献[9]用动力学系统方法对模型(1)的稳定性进行了分析.由于平衡态的数据在实际中很难观测到，故先将系统线性化，即在平衡态

(2)

线化模型(1)后再进行研究，进而给出模型(1)无拥堵的充分条件：

(3)

许多学者对这一模型进行了优化或改进[10-13].Huijberts[13]对条件(3)进行了分析，认为这一条件仅仅是一个充分条件，而不是必要条件，于是他给出并证明模型(1)稳定的充分必要条件为：

(4)

Wilson[14]比较系统地总结了跟驰模型的线性稳定性分析方法，以及对应的稳定性条件，并指出下列一般性模型一定是短波稳定的：

(5)

(6)

就一般形式的跟驰模型(5)而言，条件(6)只是一个充分条件.本文试图给出该模型稳定的充分必要条件，进而说明充分条件(6)的局限性,以及给出必要条件的重要性.

1 模型(5)的稳定性条件及其证明

将模型(5)线性化，得到ξn的线化方程：

其中，ξ=(ξ1,ξ2,…,ξn)T,η=(η1,η2,…,ηn)T，0为n×n零矩阵，I为n×n单位矩阵，

故设扰动系统的解为：

由zξ=η,zη=Aξ+Dη，得：

z2ξ=Aξ+zDξ.

于是可以得到特征方程：

det|z2I-zD-A|=0,

即

p(z)=(z2+(p2-p3)z+p1)N-(p2z+p1)N=0.

(7)

显然，当N=1时，p(z)=0的非零根z=p3恒为负,即在周期边界条件下道路上只有一辆车时，车流是稳定的.为分析N>1时的车流稳定性，本文先给出以下引理：

引理1记s=z2+mz=x+iy，其中x,y为实数，则特征方程(7)非零根实部均为负数的充分必要条件为：

由非线性系统的稳定性理论可知，系统(5)稳定的充分必要条件为：

即

(8)

又因为

将r代入，两边平方并化简得：

定理1模型(5)的稳态流稳定的充分必要条件为：

(9)

证明记

则q(s)=0的非零根可表示为：

于是有：

由引理1可知，模型(5)的特征方程根实部为负的充分必要条件为上式小于零，从而得出系统(4)稳定的充分必要条件为：

(10)

其中,k=1,2,…,N.

当k=1时,条件(10)就是条件(9).只要证明若k=1时条件(10)成立，再推出k=2,3,…,N时条件(10)也成立即可(因为本文要证明的结论与k无关，也就是k=1的情形).事实上，当k=1时，条件(10)成立，即

则k=2,3,…,N时，有：

所以，条件(10)对所有k=1,2,…,N成立的充分必要条件为条件(10)对k=1时成立.于是得到系统(5)稳定的充分必要条件为：

即

2 结论与例析

本文分析和研究了下列一般形式的车辆跟驰模型的稳定性：

本文从数学的角度给出了该模型稳定的一般性结论，并推广了已有的结果，为分析该模型的稳定性提供了一般性的理论依据.

下面分析充分必要条件(9)的两个极端情形：

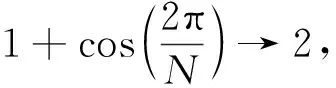
(11)

(11)式正是现有文献中的结果.

上述分析表明，现有文献中的稳定性条件只有当N→∞时才是必要的.

(12)

模型(12)稳定的充分必要条件为：

(13)

条件(13)与文献[6]所述的条件等价，进一步说明条件(9)的一般性，也从侧面验证了条件(13)的准确性.

推论2速度差模型[8]：

(14)

稳定的充分必要条件为：

(15)

速度差模型在车辆跟驰模型中有一定的代表性，在以往的稳定性分析中，学者们往往只给出模型(14)的一个必要条件：

(16)

显然，条件(15)比条件(16)更精确.