基于CM-IA算法的DOA估计最优阵列搜索方法研究

高 璐

(湖州师范学院 信息工程学院，浙江 湖州 313000)

波达方向(direction of arrival, DOA)估计[1-2]接收天线可分为均匀线阵[3]和非均匀线阵两种布放方式[4-6].均匀线阵具有结构简单、建模方便等优点，但需通过增加天线个数来提高天线的测角分辨率，极大地增加了成本，且在极高频率下阵元之间易产生互耦现象.在阵元数相同的条件下，非均匀线阵能够通过阵元的合理布放来扩大阵列孔径，同时提高DOA估计的测角分辨率，并降低阵元间的互耦效应.但非均匀线阵的阵列结构无法轻易改变，很难适用于极端环境.为能在极端环境中灵活布放阵元，诸多智能算法[7-8]被应用于DOA估计阵列结构优化中.

粒子群算法[9-10]能够在一定范围内进行多点搜索，但易发散、精度不高.模拟退火算法[11-12]在理论上是全局最优算法，但部分收敛条件几乎无法实现.蚁群算法[13-14]通用性较好，但搜索时间冗长且易停滞.遗传算法[15-17](genetic algorithm，GA)具有良好的并行性和兼容性，因此得到了广泛的应用.但其整个迭代过程是随机的，且没有指导性搜索，当后代双亲基因较近时，后代基因改善较小，造成基因模式的单一性，从而影响进化历程，甚至导致种群退化及早熟现象.免疫遗传算法作为遗传算法的重要分支，在一定程度上能够抑制种群退化现象，其疫苗的选择和接种直接决定了子代个体的适应度.但目前疫苗多为主观随机选择，易出现收敛局部最优值等问题.

近年来，许多学者对免疫遗传算法进行了更新和改进.于文莉等[18]提出将BP算法与免疫遗传算法相结合，解决遗传算法过早收敛局部最优值问题，但BP神经网络的选择无统一指导，易出现过度拟合等现象；马佳等[19]提出的免疫克隆算法，解决了遗传算法局部搜索能力差等问题，但随着种群数目的增加，该算法耗时巨大；江务学等[20]通过优化交叉、变异算子实现了遗传算法的多目标问题优化，但其仅限于特定优化问题，不具备通用性.

混沌系统自1963年问世至今得到了快速的应用和发展[21-22].Deng等[23]引入一种用于数字域的混沌迭代方程，该方程能够随着数字域的混沌迭代方式更新，具备周期性、遍历性，以及依赖于初始参数值等特点，从而被广泛应用于自迭代产生运算组合的伪随机序列算法中[24-26].可见，混沌方程可应用于疫苗选择机制中的免疫遗传算法.

针对目前DOA估计阵列布放存在灵活性差，不适用于极端环境，且在遗传算法中易出现早熟和混沌方程鲜少用于遗传算法的现状，本文根据遗传算法的自迭代过程，设计一种混沌方程产生的伪随机序列，合理设置初始值，改进疫苗的制作和提取方法，提出一种基于混沌因子的免疫遗传算法(Immune Genetic Algorithm based on Chaotic Mechanism，CM-IA)，用于搜索DOA估计的最优阵列.

1 CM-IA算法原理

1.1 建立初始阵列种群

设阵列孔径为B，初始种群规模为z.对初始种群中的阵列结构进行二进制编码，1表示该基因位布放阵元，反之则不布放阵元.基因位1和基因位L编码均为1.当远场窄带信号S(t)分别从方向{θ1,θ2,…,θP}入射时，依次利用初始种群中各个阵列接收信号S(t)，计算其数据协方差矩阵R：

R=ARSAH+σ2I，

(1)

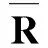
(2)

1.2 阵列结构的交叉与变异

基于轮盘赌法则，第i个阵列结构以概率Pi被选择参与种群进化，如式(3)所示：

(3)

其中，Fi为阵列结构适应度的值.随机生成ni,ni∈[0,1]，当Pi>ni时，Pi对应的第i个阵列结构被选中参与进化.再次生成z个随机数ni,ni∈[0,1]，当Pc>ni时，ni对应的阵列结构参与交叉运算.

1.3 基于混沌因子的疫苗接种

根据DOA估计阵列结构的布放特征构造混沌方程，如式(4)所示：

ui=4ui-1(1-ui-1)，

(4)

其中：i=z(g-1)+1,z(g-1)+2,…,z(g-1)+z；g为迭代次数.基于混沌因子产生混沌初值u0，为能在获取随机序列的同时避免混沌方程产生的随机数收敛于同一数值，将混沌初值u0设为u0∈[0,1]，且u0∉{0,0.25,0.5,0.75,1}.从母本阵列结构中分i次选择部分基因片段ci制成疫苗，再根据混沌方程将疫苗更新.如式(5)所示：

ci=Lui，

(5)

将基于混沌因子的疫苗接种至阵列个体形成抗体，抗体阵元数保持为M.

基于Metropolis法则，若接种疫苗后，阵列个体的适应度值变大，则接受注射疫苗后的阵列结构作为新种群的个体；反之，则以概率Pa(i)接受接种疫苗后的阵列结构.如式(6)所示：

(6)

其中，ΔE为注射疫苗前后阵列个体的适应度差值.

图1 CM-IA算法流程图Fig.1 Flow diagram of CM-IA algorithm

基于Metropolis法则，将选出的阵列结构按照适应度值的大小排列，筛选出适应度值最低的阵列结构；根据精英保留原则，利用父代适应度值最高的阵列结构取代本代适应度值最低的阵列结构，更新种群直至最大迭代次数，最终输出最优个体，其对应的阵列结构即为该限定条件下的DOA估计最优阵列结构.CM-IA算法流程如图1所示.

2 仿真实验与算法性能分析

为验证本文所提出的CM-IA算法的有效性，利用Matlab软件平台进行以下两个仿真实验：

2.1 仿真实验一

将阵列孔径约束为4.5λ,种群规模为80,天线数为10,基因位共37位,变异概率Pm为0.004,交叉概率Pc为0.5.当空间中两个相互独立的远场窄带信号分别从方向15°和25°入射时，利用MUSIC算法对上述信号进行谱峰搜索，并将DOA估计均方根误差的倒数作为适应度函数，再分别利用本文提出的CM-IA算法和经典免疫遗传(IA)算法搜索DOA估计最优阵列结构.两种算法的适应度函数变化趋势如图2所示.

图2 DOA估计适应度值随迭代次数的变化趋势Fig.2 Trend of fitness value of DOAestimation with iteration times

由图2可知，当迭代次数相同时，CM-IA算法的适应度值高于IA算法;当迭代次数约达83时，IA算法停止进化，适应度值约为68;当迭代次数达到90时，CM-IA算法停止进化，适应度值约为77.CM-IA算法搜索得到的个体适应度值明显高于IA算法.可见，CM-IA算法能够避免传统IA算法的早熟现象，且进化所得的最优个体能够获得更高的适应度.

CM-IA算法经过100次迭代所获得的该环境下最优个体为[1 0 0 0 1 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1].

2.2 仿真实验二

图3 不同信噪比条件下DOA估计成功概率的变化趋势Fig.3 Trend of DOA estimation success probability under different SNR

由图3可知，利用OMP算法分辨两个相干信号的来波方向，当信噪比低于10 dB时，在该约束条件下CM-IA算法优化所得的最优阵列结构DOA估计的成功概率远高于10元均匀线阵；当信噪比达到13 dB时，两种阵列结构的DOA估计成功概率趋于一致.SS-MUSIC算法在处理相干信号时，由于损失了大量的阵列孔径，在小快拍数的条件下无法利用10元均匀线阵分辨出空间远场窄带信号，当阵元数增大至20、信噪比提高至30 dB时，成功概率才能达到1.可见，在一定条件下与相同阵元数的均匀线阵相比，CM-IA算法搜索得出的最优阵列结构充分地利用了阵列孔径，在小快拍数、低信噪比的恶劣条件下能够获得更高的DOA估计成功概率，且能推广应用于OMP等压缩感知算法中关于相干信号的处理，避免了传统SS-MUSIC算法处理相干信号所需快拍数大、信噪比高等弊端.

3 结 语

本文将混沌机制应用于遗传算法，提出CM-IA算法用于搜索一定约束条件下DOA估计的最优阵列结构，并将DOA估计均方根误差的倒数作为适应度函数，通过构建混沌方程和设置混沌初值得到了一组非随机序列.根据混沌方程所得的混沌因子制作疫苗并为个体接种，通过交叉和变异运算实现种群的更新，最终输出的最优个体即为DOA估计最优阵列结构.仿真结果表明，与IA算法相比，CM-IA算法能够获得适应度更高的阵列结构.该阵列结构与均匀线阵相比，能够充分利用阵列孔径提高DOA估计的成功概率，且能够推广应用于压缩感知算法中关于相干信号的处理，实现DOA估计阵元的灵活布放，极大地增加了阵列结构的利用率.