基于区间直觉梯形模糊数的集群企业知识共享博弈研究

肖汉杰,鲍舒燕,韦 震,唐洪雷,周建华

(1.湖州师范学院 经济管理学院，浙江 湖州 313000；2.昆明理工大学 复杂有色金属资源清洁利用国家重点实验室，云南 昆明 650093)

0 引 言

目前中国正面临经济发展降速和社会环境问题严峻的双重压力，打造世界级产业集群，向全球价值链中高端迈进，成为高质量经济发展的重要战略支点[1].在知识经济时代，创新是产业集群面对全局经济一体化竞争生存、发展和升级的必然选择[2-3].企业知识共享行为是产业集群能够突破全球价值链中低端锁定的关键活动[4]，也是国内外学术界研究的焦点.

当前我国集群内各创新行为主体间的关系松散，分工与合作的基础不稳固，没有建立严格的契约关系，知识共享主体之间信任程度不高[5-6].作为有限的理性主体，集群企业总是希望对方先采取策略，而自身则采取搭便车和投机的行为，同时由于难以规避知识共享溢出的损失，阻碍了知识共享行为的产生，由此陷入“囚徒困境”[7-8].实质性的知识共享合作必须建立在对各博弈主体收益充分考虑的基础上[5].国外学者Shih等[9]、Vries等[10]和Estrada等[11]对产业集群知识共享影响因素、知识共享与企业创新绩效的研究取得了较大进步，为产业集群知识共享研究做出了重要贡献.近年以数学为基础的博弈论被引入知识共享利益冲突与矛盾的决策中.关于集群内企业与外部企业之间的知识共享博弈研究，米捷等[12]、Turkina等[13]、韩莹等[14]探讨了知识势差、投机行为、政府补贴等因素对局中人决策的影响，并提出了对策与建议；关于集群供应链中横向企业间知识共享博弈的研究，李煜华等[15]、王朋举[16]、Ganguly等[17]、王永明等[18]从供应链视角探讨了集群内企业的博弈行为，以及知识溢出效益、投机行为、资源禀赋等因素对局中人策略的影响，并提出了关于合作失败预防和提升合作效率的对策与建议.上述研究为破解产业集群内企业知识共享“囚徒困境”探寻了企业内部治理、政府引导和第三方介入等多种路径，较好地指导了企业知识共享行为决策.然而，由于企业的决策过程总是在有限的信息下完成的，再加上企业认知水平的局限性，以及面临外部复杂信息的影响，知识共享博弈局中人的策略选择受到很大影响，使得企业难以对知识共享策略收益进行精确估计，实际决策总在模糊条件和信息下完成，博弈双方难以在策略选择中选出最优策略[19].上述研究较少探索知识共享过程中企业决策的不确定性问题.近年随着模糊集合理论在决策分析领域的研究与应用，研究博弈论中的不确定性问题有了新的思路与方法.Campos等[20]、万树平等[21]和李霞等[22]给出了详细的基于模糊数的博弈最优解证明，确保了均衡策略求解的科学性.刻画模糊性有模糊数、区间数和三角模糊数等.研究发现，梯形模糊数形式丢失的信息最少[21]，但其隶属度函数对客观事物的刻画较为粗糙，而区间模糊数描述隶属度显得更加细腻和灵活[23].本研究首先引入区间直觉梯形模糊数(IITFN)，构建支付函数矩阵，并分析纯策略与混合策略最优解的求取方法；然后结合产业集群企业知识共享的实际问题构建基于区间直觉梯形模糊数的知识共享博弈模型，并分析企业知识共享策略的选择和条件；最后提出促进集群企业知识共享的对策与建议.

1 基于IITFN的博弈理论模型

1.1 区间直觉梯形模糊数的定义

在局中人决策过程中，双方是在非完全信息下完成的，都需要通过试错、学习来进行决策.在此过程中，决策者无法规避有限的理性和心理因素，但采用准确值构建博弈支付矩阵存在一定不足.而结合区间数和梯形模糊数的优势描述局中人策略支付函数，使得博弈过程与现实更加贴切，博弈结果与实际情形更加接近.区间直觉梯形模糊数的构造方法如下：

定义1[21]设为实数集，X⊂为非空数集，论域U为连续集，则称：

(1)

(2)

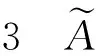
(3)

1.2 基于IITFN的博弈最优策略

基于IITFN的博弈模型是指采用区间直觉梯形模糊数替代精确值刻画局中人策略选择对应的博弈支付函数.基于IITFN的博弈模型可记为：

(4)

其中：S1={α1,α2,…,αm}、S2={β1,β2,…,βn}分别为局中人I、II的策略集合；m和n分别为局中人I、II的策略集合.该博弈系统的纳什均衡和最优策略解证明见文献[22].以两两博弈为例，局中人I选择策略α1、α2的概率分别为p、1-p；局中人II选择策略β1、β2的概率分别为q、1-q.基于IITFN的博弈支付函数见表1.

表1 局中人博弈支付矩阵

根据表1中的局中人博弈支付矩阵，结合纳什定理可知,局中人I与局中人II的博弈存在唯一最优混合策略解，见式(5)：

(5)

为确保式(5)有意义，需满足式(6)：

(6)

满足式(6)即获得了基于IITFN的博弈最优策略解：{p*,q*}.

2 基于IITFN的集群企业知识共享博弈

2.1 模型假设

集群企业知识共享策略的选择与其市场竞争策略和自身战略有关.产业集群内企业知识共享系统是一个相互影响的相对独立系统[16,18].在企业知识共享合作中，集群内企业间的合作关系较为松散，没有严格的契约关系，企业难以获取对方企业隐性的知识信息和真伪，因此合作是在信息不完全的条件下进行的，其知识共享主体间信任度不高，合作决策过程存在模糊性，需要不断地观测对方的决策和行为来试错、学习后进行决策.基于上述决策模糊的特征，本研究假设如下：

假设1：产业集群知识共享博弈系统可以简化为2×2的博弈类型.产业集群内的企业可以分为两类有限的理性群体：群体A和群体B.从群体A中抽取的企业称为企业A，从群体B中抽取的企业称为企业B.集群企业的合作是否进行知识共享，决策的依据是自身利益的最大化.

假设2：企业A和企业B都有两种选择：共享策略(S1)和不共享策略(S2).假设企业A选择策略S1的概率为x，则选择策略S2的概率为1-x；企业B选择策略S1的概率为y，则选择策略S2的概率为1-y.x、y均为时间t的函数.

2.2 模型构建

集群企业A和企业B是否进行知识共享，是依据对方的策略选择和自身利益最大化来决策的.根据上述假设，集群企业在博弈过程中是无法获得完整信息的，因此决策过程具有模糊特征.根据研究假设得到的支付函数矩阵见表2.

表2 博弈双方的支付函数矩阵

根据表2，采用微积分求极值，得到集群企业采取策略S1的概率表达式：

(7)

根据式(7)可知，企业的知识策略受共享成本、知识吸收能力、投机概率和知识共享增益等参数的影响.

2.3 实例分析

结合式(6)进行数值模拟仿真，获得不同参数下双方选择知识共享策略的概率.仿真参数见表3.

表3 假设参数模糊值与各策略收益

当策略组合为{S1，S1}时，企业A的支付函数为：

[13,23,35,52]，[0.4,0.7]，[0.3,0.5]；

企业B的支付函数为：

[12,21,32,45]，[0.2,0.5]，[0.3,0.4].

当策略组合为{S1，S2}时，企业A的支付函数为：

企业B的支付函数为：

当策略组合为{S2，S1}时，企业A的支付函数为：

[9,15,26,44]，[0.1,0.3]，[0.2,0.4]；

企业B的支付函数为：

[9,14,24,41]，[0.1,0.2]，[0.3,0.4].

当策略组合为{S2，S2}时，企业A的支付函数为：

[6,8,10,12]，[0.1,0.2]，[0.3,0.4]；

企业B的支付函数为：

[10,12,14,16]，[0.2,0.4]，[0.3,0.4].

根据博弈均衡求解得到的混合策略最优解为：

3 结 论

针对产业集群内企业合作关系松散、知识共享效率低的问题,本研究基于双方在合作过程中决策的模糊特征，引入区间数和直觉梯形模糊数,刻画双方策略选择的支付函数，构建基于IITFN的产业集群企业知识共享博弈模型，并通过算例分析不同条件下集群企业选择知识共享策略的概率.研究结果如下：

(1)在知识共享策略选择过程中，集群企业总是在不完全的信息条件下进行的，决策过程具有模糊性.而引入区间数和直觉梯形模糊数刻画双方策略选择的支付函数,所得的博弈结果更贴近现实.

(2)在知识共享策略选择过程中，作为有限理性人，由于知识溢出的存在，集群企业总是偏向于采取投机和搭便车的行为，在没有政府规制的引导下，博弈系统很可能陷入“囚徒困境”，知识共享合作难以达成.因此，促进企业知识共享的关键是降低集群企业的投机和搭便车行为.

产业集群内企业虽然在区域内形成了较为紧密的联系，但在实际合作过程中信息不对称的现象普遍存在，企业间的合作关系并不紧密.因此，产业集群知识共享必须建立有效的契约关系，一是可以借助区块链技术建立智能合约，增强双方合作信任；二是要加强合作监督，政府部门在法律法规制定和对产业集群联盟的内部治理上，要对企业合作的投机行为、失信行为采取严格的惩罚措施，从而为产业集群知识共享创建良好环境.