反双纽线正弦函数的渐近不等式

张依婷，王淼坤

(湖州师范学院 理学院,浙江 湖州 313000)

0 引 言

众所周知，在平面直角坐标系下，伯努利双纽线标准方程为(x2+y2)2=x2-y2,其弧长公式可表示为4arcsl(1),其中arcsl(x)是著名的反双纽线(三角)正弦函数，定义为[1-3]：

由文献[3]中的定理1.7表明:

近年来，利用二元平均值研究特殊函数的渐近性质及不等式是一种非常有效的方法[4-5].本文将在平均值理论中探究反双纽线正弦函数满足的新不等式,并引入与本文研究相关的几个二元平均值.

设p∈,两个正数a和b的p阶幂平均定义为：

2015年，Witkowski[6]引入Seiffert函数，给出了一族二元平均值——Seiffert型平均值.特别地，若令Seiffert函数为反双纽线(三角)正弦函数，可得如下的反双纽线正弦平均值Marcsl(a,b)：

对p∈和s≥1，定义两个正数a和b推广的p阶幂平均为：

并记以下几个特殊情形：

2017年，王根娣等[7]建立了反双纽线正弦函数的Shafer-Fink型不等式：

不难发现，上述两个不等式可表示为反双纽线正弦平均值Marcsl(a,b)与推广的p阶幂平均之间的平均值不等式，即当a,b>0且a≠b时，

更多关于反双纽线正弦函数的不等式，如Wilker型不等式、Huygens型不等式见文献[8-10].

定理1设α,β∈(0,1)，不等式

对所有a,b>0,a≠b均成立，当且仅当α≤α0=8/27及β≥β0=10/(9ω)≈0.848.

定理2设λ,μ∈(0,1)，不等式

对所有a,b>0,a≠b均成立，当且仅当λ≤λ0=2/3及μ≥μ0=5/(4ω)≈0.954.

在定理1和定理2中，令a=1+x,b=1-x,可得到以下结论：

结论当x∈(0,1)时,不等式

成立，其中,10/(9ω)≈0.848,8/27,5/(4ω)≈0.954和2/3是满足上述不等式成立的最佳参数.

1 引 理

为证明本文的主要结果，建立以下两个引理：

引理1设p∈(0,1)，定义(0,1)上的函数

则下列论断成立：

(Ⅰ)当α0=8/27时，Gα0(x)>0且Gα0(x)在(0,1)上严格单调增加；

(Ⅱ)当β0=10/(9ω)时，Gβ0(x)<0且存在x0∈(0,1),Gβ0(x)在(0,x0)上严格单调减小，在(x0,1)上严格单调增加.

证明计算得：

(1)

(2)

其中，

(3)

Hp(0+)=40-40p,Hp(1-)=0.

(4)

下面分p=α0和p=β0两种情况进行讨论:

情形1p=α0,则由式(3)得：∀t∈(0,1),

(5)

结合式(1)和式(2)知,Gα0(x)在(0,1)上严格单调增加，且Gα0(x)>0对所有的x∈(0,1)均成立.

情形2p=β0,则

Hβ0(t)=-β02t24-30β0t19+20β0(β0-1)t15-18β02t14+60(-β0+1)t10+
130β0t9-100(β0-1)2t6+180β0(β0-1)t5-81β02t4+40-40β0.

(6)

计算得：

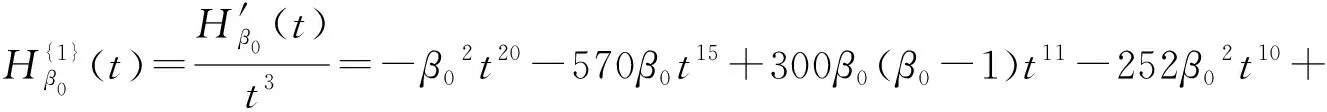
(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

由式(6)～(14)可推断Hβ0(t)在(0,1)上的单调性和正负性,结果见表1.

表1 Hβ0(t)在(0,1)上的单调性和正负性

结合式(2)可知,存在x0∈(0,1),当x∈(0,x0)时G′β0(x)<0;当x∈(x0,1)时G′β0(x)>0.因此,Gβ0(x)在(0,x0)上严格单调减小,在(x0,1)上严格单调增加.最后,由式(1)及Gβ0(x)在(0,1)上的分段单调性,可推断Gβ0(x)<0对所有的x∈(0,1)均成立.

引理2设p∈(0,1)，定义(0,1)上的函数

则下列论断成立：

(Ⅰ)当λ0=2/3时，Iλ0(x)>0且Iλ0(x)在(0,1)上严格单调增加；

证明计算得:

(15)

(16)

其中,

Jp(t)=-p(5+p)t14+5(2p2-5p+3)t10+4p(5-2p)t9-
25(p-1)2t6+40p(p-1)t5+2p(5-8p)t4+10(1-p),

(17)

Jp(0+)=10-10p，Jp(1-)=0.

(18)

下面分p=λ0和p=μ0两种情况进行讨论:

情形1p=λ0,则由式(16)得：∀t∈(0,1),

(19)

结合式(15)和式(16)知,Iλ0(x)在(0,1)上严格单调增加,且Iλ0(x)>0对所有x∈(0,1)均成立.

情形2p=μ0,则

Jp(t)=-μ0(5+μ0)t14+5(2μ02-5μ0+3)t10+4μ0(5-2μ0)t9-
25(μ0-1)2t6+40μ0(μ0-1)t5+2μ0(5-8μ0)t4+10(1-μ0),

(20)

计算得:

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

由式(20)～(28)可推断Jμ0(t)在(0,1)上的单调性与正负性，结果见表2.

表2 Jμ0(t)在(0,1)上的单调性与正负性

2 主要结果证明

设p∈(0,1)，则

其中，Gp(x)同引理1.

下面分两种情形进行讨论：

情形Ap=α0=8/27,则由引理1(Ⅰ)得：当x∈(0,1),Gα0(x)>0.因此,当a,b>0且a≠b时，不等式

成立.

情形Bp=β0=10/(9ω)≈0.848,则由引理1(Ⅱ)得：当x∈(0,1)时,

Gβ0(x)

因此,当a,b>0且a≠b时，不等式

成立.

最后证明α0=8/27及β0=10/(9ω)是满足定理1中不等式的最佳常数.事实上，将Gp(x)在x=0处Taylor展开得:

由此表明，要使不等式

对所有a,b>0且a≠b成立,仅当p≤8/27.

另一方面，由引理1知，

因此，不等式

对所有a,b>0且a≠b成立,仅当p≥10/(9ω).

定理1得证.

设p∈(0,1)，则

其中Ip(x)同引理2.

下面分两种情形进行讨论：

情形Ap=λ0=2/3,则由引理2(Ⅰ)得：当x∈(0,1)时,Iλ0(x)>0.因此,当a,b>0且a≠b时，不等式

成立.

情形Bp=μ0=5/(4ω)≈0.953 5,则由引理2(Ⅱ)得：当x∈(0,1)时,

Iμ0(x)

因此，当a,b>0且a≠b时，不等式

成立.

最后证明λ0=2/3及μ0=5/(4ω)是满足定理2中不等式的最佳常数.事实上，将Ip(x)在x=0处Taylor展开得:

由此表明，要使不等式

对所有a,b>0且a≠b成立,仅当p≤2/3.

另一方面，由引理2知:

因此不等式

对所有a,b>0且a≠b成立,仅当p≥5/(4ω).

定理2得证.